混合动力汽车回馈制动与防抱死制动协调鲁棒控制*
2015-04-12金贤建殷国栋王金湘
金贤建,殷国栋,2,陈 南,王金湘
(1.东南大学机械工程学院,南京 211189; 2.重庆大学,机械传动国家重点实验室,重庆 400044)
2015174
混合动力汽车回馈制动与防抱死制动协调鲁棒控制*
金贤建1,殷国栋1,2,陈 南1,王金湘1
(1.东南大学机械工程学院,南京 211189; 2.重庆大学,机械传动国家重点实验室,重庆 400044)
提出了一种并联式混合动力汽车防抱死制动系统(ABS)和能量回馈制动的协调控制策略。针对防抱死制动系统的强非线性和时变特征,设计了基于滑移率切换面的ABS滑模变结构控制器。为削弱传统滑模控制中的颤振和补偿模型的不确定性,采用指数趋近率方法来改善滑模运动段的动态品质和鲁棒性;能量回馈制动系统中,电池SOC、电机转速和制动强度等动态参数的影响较大,因此,采用T-S模糊逻辑控制策略动态调节电机制动转矩来提高制动能量的回收率。在Matlab/Simulink环境中建立整车制动系统模型,对所提出的协调控制策略在紧急制动和NEDC工况下进行仿真。结果表明:该策略在保证车辆制动稳定性的同时,能有效地提高制动能量的回收率,且具有较强的鲁棒性。
混合动力汽车;回馈制动;防抱死制动;滑模变结构控制;T-S模糊控制
前言
并联式混合动力电动汽车的制动系统由传统的液压制动系统和回馈制动系统两部分组成。在回馈制动过程中,电动机以发电方式工作,能将汽车的动能或势能转换为电能进行存储,实现了能量回收再利用,有效地改善了车辆的燃油经济性和排放性能。
目前国内外对混合动力电动汽车制动系统的研究主要集中在如何使能量回馈效率最大化:一方面的研究是根据限制回馈制动的因素如电池SOC、电机转速等来采取相应的控制策略提高能量回馈效率[1-3];另一方面的研究是通过连续调节金属带式无级变速器(CVT)速比控制发电机工作在高效率区来提高发电效率,进而提高制动能量回收率[4-5]。而对同时保证车辆制动稳定性和提高回馈制动能量效率的集成协调控制策略的研究尚处于起步阶段。
本文中针对装有CVT、永磁同步电机和NiMH电池组的前驱并联式混合动力汽车,提出了一种防抱死制动系统(ABS)和能量回馈制动的集成控制策略,并通过仿真验证了协调鲁棒控制策略在混合动力汽车制动系统中的可行性和有效性。
1 系统模型
1.1 半车动力学模型
纵向制动过程不考虑车身侧倾和车轮转向角,采用半车模型的车辆动力学方程为
(1)
(2)
(3)
Fxi=μ(λ)Fzi
(4)
(5)
(6)
式中:M为整车质量;v为车辆速度;Fx为纵向摩擦力;Fa为空气阻力;Ff为滚动阻力;Jω为车轮转动惯量;ωF和ωR为前、后轮角速度;R为车轮半径;FxF和FxR分别为前、后轮纵向摩擦力;TfF和TfR分别为前、后轮滚动阻力矩;ThF和ThR分别为前、后轮液压制动力矩;Tm为电机制动转矩;i=F,R分别表示前、后轮;μ(λ)为车轮纵向附着系数;FzF和FzR为地面对前、后轮的垂直反作用力;lR和lF为质心距前、后轴距离;L为轮距;hg为车辆质心高度。
1.2 轮胎模型
采用魔术公式(Pacejka)轮胎模型模拟制动时车轮纵向附着系数和车轮纵向滑移率之间的关系[6]:
μ(λ)=θsin{Carctan[Bλ-E(Bλ-
arctan(Bλ))]}
(7)
λ=(v-ωR)/v
(8)
式中:θ为峰值因子;C为曲线形状因子;B为刚度因子;E为曲线曲率因子;ω为车轮角速度;λ为车轮纵向滑移率。用魔术公式拟合干沥青、湿鹅卵石路面的μ-λ非线性曲线如图1所示。
1.3 电机模型
高功率密度、高效率和宽调速的车用电机是混合动力汽车关键技术之一,永磁同步电机具备无励磁损失、调速性能好、功率密度大和控制精度高等优点,已引起各大电动汽车厂家和科研机构的重视。本文中选用永磁同步电机作为车载电机。永磁同步电机从静止三相坐标系ABC经Clarke变换得到静止两相α-β坐标系,再经Park变换得到两相旋转d-q坐标系,其电压方程[7]为
(9)
其中磁链方程:
(10)
电磁转矩方程:
(11)
式中:ud和uq分别为永磁同步电动机直轴、交轴的电压;id和iq分别为直轴、交轴的电流;Ra为定子绕组的电阻;P为微分算子d/dt;ωr为永磁同步电动机感生电动势的电角速度;Ψd和Ψq分别为永磁同步电动机的直轴、交轴磁链;Ld和Lq为电机的直、交轴电感;p为极对数;Ψf为d-q轴系统中电机的空载永磁磁链。
电机系统的运动方程为
(12)
式中:j,TL和c分别为转动惯量、负载转矩和机械阻尼系数。电机驱动/制动总效率如图2所示。
1.4 电池模型
利用马斯定律计算出当前的充电电流,再采用安时累计法计算SOC值:
(13)
式中:电流I为负值时,电池充电;SOC0为初始SOC值;Kt为温度增益系数;Cn为电池额定容量。结合电池试验数据,得到电池SOC、内阻和温度的关系如图3所示。
1.5 液压系统模型
制动系统液压部分包括液压传动系统和制动器两部分。利用试验数据能较准确地描述迟滞非线性的ABS液压传动系统的动态过程[8]:
(14)
式中:pm为制动主缸压力;pωi为制动轮缸压力;pr为低压蓄能器中的液压。
制动器的数学模型为
(15)
式中:Th为液压制动力矩;Kd为制动效能因子;Ab为活塞面积;r为有效制动半径;ξ和ωn分别为制动器的阻尼系数和固有频率。
2 制动系统集成控制策略
混合动力汽车制动系统集成控制策略的设计目标是实现回馈制动力矩和液压制动力矩的协同工作,从而在保证车辆制动稳定性的前提下有效地提高制动能量的回收率。在集成控制策略中,基于滑移率切换面的ABS滑模变结构控制器能将车轮的滑移率稳定在该附着系数路面的最优滑移率附近来保证车辆的制动稳定性能,基于电池SOC、电机转速和制动强度的T-S模糊逻辑控制策略能通过动态调节电机制动转矩有效提高制动能量的回收率。制动系统集成控制策略结构如图4所示。Tr代表需求的制动力矩,Tmm代表电机制动系统能够施加的最大制动力矩,β代表电机的负载比,则有下式成立:
Tr=Th+βTmm
(16)
2.1 防抱死制动滑模变结构控制
防抱死制动系统滑模变结构控制器的目标是设计液压制动力矩的控制律,使车轮滑移率跟踪期望滑移率,具体设计分为切换控制和等效控制两部分。根据汽车制动系统模型,定义状态变量:
x1=v;x2=ω;x3=λ=(x1-Rx2)/x1
(17)
则有
(18)
定义切换函数:
s=λ-λr
(19)
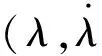
(20)
则得到等效控制:
(21)
为削弱传统滑模控制中的颤振,改善滑模运动段的动态品质和鲁棒性,本文中采用指数趋近率:
(22)
为满足滑模变结构控制的到达条件,构造到达条件的Lyapunov函数:
V=s2/2
(23)
μ(λ)f6(x3))-εsgn(s)-ks]}=-f7(x1)ε|s|-ks2
(24)
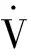
由式(18)得
Fp(λ,t)+Gp(t)u(t)
(25)
其中: Fp(λ,t)=f5(x1,x2)-μ(λ)f6(x3)
Gp(t)=f7(x1);u(t)=Th
根据式(25),系统的标称模型可写为
(26)
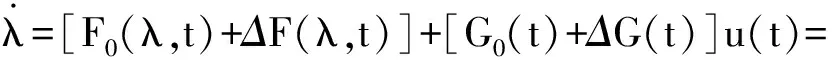
(27)
式中:ΔF(λ,t)和ΔG(t)为系统的不确定量;W为系统集中不确定量,定义为W=ΔF(λ,t)+ΔG(t)u(t),且满足|W|≤K,K为集中不确定量的上界,则K补偿了模型的不确定性。
(28)
2.2 回馈制动模糊逻辑控制
模糊逻辑控制是借助于模糊集合理论将被输入量模糊化,经过模糊规则推理、输出量清晰化处理后实现输出量对被控对象进行智能控制的方法。这里采用T-S模糊逻辑控制策略动态调节电机制动转矩以有效提高制动能量的回收率,回馈制动模糊控制器的输入为电池SOC、电机转速n和制动强度z,输出为电机的负载比β。输入、输出变量均被5个模糊子集模糊化,5个模糊子集为[TL,L,M,H,TH],依次分别表示为太低、低、中、高和太高,输入、输出变量的隶属度函数均采用三角型,如图5所示。模糊规则使用Zadeh的模糊逻辑AND操作,采用T-S模糊推理和mom反模糊化得到输出。输入、输出的模糊推理规则曲面如图6所示。
3 仿真与分析
为评估集成控制策略的效果,利用Matlab/Simulink平台对混合动力电动汽车的集成控制策略进行仿真,仿真工况分为紧急制动和NEDC工况两种,其中紧急制动工况侧重对控制策略的有效性、稳定性和鲁棒性进行验证,而NEDC工况侧重对能量回收情况进行验证。
3.1 紧急制动工况仿真
紧急制动仿真结果如图7所示。从图7(a)和图7(b)可以看出,在紧急制动过程中,车速与轮速开始有较大的偏差,这是因为滑模控制还处于切换控制中,系统状态还未到达滑模面;指数趋近率滑模控制与传统滑模控制的车轮均没有发生抱死,车轮的滑移率在经历制动初始阶段的波动后都稳定在附着系数路面的最优滑移率处,但是,指数趋近率滑模控制与传统滑模控制相比,开始制动时车速与轮速的偏差较小,滑移率的超调量较小,滑移率的波动次数也较少,且先稳定在最优滑移率处,制动时间相对较短,这表明指数趋近率滑模控制与传统滑模控制相比,以更快的趋近速度先到达滑模面,没有发生传统滑模控制中多次穿越切换面的现象,颤振被明显削弱,且补偿了模型的不确定性,鲁棒性较强。
从图7(c)和图7(d)可以看出,液压制动力矩和电机回馈制动力矩虽然同时作用在车轮上,但在紧急制动的初始阶段,为了保证制动的稳定性,液压制动力矩远大于电机的回馈制动力矩,随着车速的变化,电/液两种制动力矩进行动态调整,为了回收更多的能量,电机回馈制动力矩随着车速的降低而增大,而在确保制动安全性后,液压制动力矩随着车速的下降而减小,这表明液压与回馈两种制动系统协同工作良好。
3.2 NEDC工况仿真
NEDC工况仿真结果如图8所示。从图8可以看出,在NEDC工况正常制动过程中,电机回馈制动力矩比液压制动力矩大,这说明在正常制动过程中回馈制动起主要作用;整个NEDC工况完成后,模糊逻辑控制的SOC值较传统控制高,模糊逻辑控制回馈能量380kJ,传统控制回馈能量330kJ,模糊逻辑控制回馈能量较传统控制增加了15.2%,这说明模糊逻辑控制策略能明显提高回馈制动的能量回收率。
4 结论
本文中针对并联式混合动力汽车制动系统,提出了一种防抱死制动(ABS)和能量回馈制动的集成控制策略,设计了基于指数趋近率的ABS滑模变结构控制器和T-S模糊逻辑回馈制动控制器,并对集成控制策略进行了紧急制动和NEDC工况仿真。结果表明:指数趋近率的滑模变结构控制适合于非线性、时变的汽车防抱制动系统,能够明显削弱传统滑模控制中的颤振和补偿模型的不确定性,制动稳定性能良好,具有较强的鲁棒性;T-S模糊逻辑控制能有效回收能量,明显提高制动能量的回收率。虽然仿真结果验证了提出的集成控制策略的正确性与有效性,但由于理论研究与实际应用还存在一些差异,因此,下一步的研究将搭建dSPACE硬件在环仿真平台,通过硬件在环仿真与实车试验来进一步验证集成控制策略的实际应用效果。
[1] Muta K, Yamazaki M, Tokieda J. Development of New-generation Hybrid System THS II-drastic Improvement of Power Performance and Fuel Economy[C]. SAE Paper 2004-01-0064.
[2] 罗禹贡,李蓬,金达锋,等.基于最优控制理论的制动能量回收策略研究[J].汽车工程,2006,28(4):356-360.
[3] Sovran G, Blaser D. Quantifying the Potential Impacts of Regenerative Braking on a Vehicle’s Tractive Fuel Consumption for the U.S., European, and Japanese Driving Schedules[C]. SAE Paper 2006-01-0664.
[4] Yeo H, Song C, Kim C, et al. Hardware in the Loop Simulation of Hybrid Vehicle for Optimal Engine Operation by CVT Ratio Control[J]. International Journal of Automotive Technology,2005,5(3):201-208.
[5] Bera T K, Bhattacharya K, Samantaray A K. Bond Graph Model-based Evaluation of a Sliding Mode Controller for a Combined Regenerative and Antilock Braking System[J]. Proceedings of the Institution of Mechanical Engineers, Part I: Journal of Systems and Control Engineering,2011,225(7):918-934.
[6] Pacejka H B, Bakker E. Magic Formula Tyre Model[J]. Vehicle System Dynamics,1993,21(1):1-18.
[7] Yin G D. Estimating Lateral Stability Region for Four Wheel Independently Actuated Electric Vehicle Considering Steering[C]. SAE Paper 2013-01-2373.
[8] Pu J H, Yin C L, Zhang J W. Fuzzy Torque Control Strategy for Parallel Hybrid Electric Vehicles[J]. International Journal of Automotive Technology,2005,6(5):529-536.
Coordinated Robust Control of Regenerative Braking andAnti-lock Braking for a Hybrid Electric Vehicle
Jin Xianjian1, Yin Guodong1,2, Chen Nan1& Wang Jinxiang1
1.SchoolofMechanicalEngineering,SoutheastUniversity,Nanjing211189; 2.ChongqingUniversity,StateKeyLaboratoryofMechanicalTransmission,Chongqing400044
A coordinated control strategy for a parallel hybrid electric vehicle equipped with antilock braking system (ABS) and regenerative braking system is proposed, and a sliding-mode variable structure controller for ABS based on slip rate switching surface is designed. For reducing the chattering in traditional sliding mode control and compensating the uncertainty of model, exponential approach law is adopted to improve the dynamic quality and robustness of sliding mode motion. The dynamic parameters like battery SOC, motor speed and braking intensity all have rather significant influences in energy regenerative braking system, so T-S fuzzy logic control strategy is used to dynamically adjust the braking torque of motor for improving the recovery rate of braking energy. A model for vehicle brake system is built with Matlab/Simulink and a simulation on coordinated control strategy is conducted with both emergency baking condition and NEDC driving cycle. The results show that the strategy proposed can effectively enhance the recovery rate of braking energy with strong robustness while ensuring the braking stability of vehicle.
hybrid electric vehicle; regenerative braking; antilock braking; sliding mode variable structure control; T-S fuzzy control
*国家自然科学基金(51105074,51375086,51205058)、机械传动国家重点实验室开放基金(SKLMT-KFKT-201206)和东南大学优秀博士学位论文基金(6BJJ1429)资助。
原稿收到日期为2013年11月8日,修改稿收到日期为2014年4月22日。
