车用质子交换膜燃料电池经济寿命的研究*

陈会翠，裴普成

(清华大学，汽车安全与节能国家重点实验室，北京 100084)



2015172

车用质子交换膜燃料电池经济寿命的研究*

陈会翠，裴普成

(清华大学，汽车安全与节能国家重点实验室，北京 100084)

本文从成本的角度提出了车用PEM燃料电池寿命的一种评价方法—燃料电池经济寿命，并建立相应的数学模型。燃料电池经济寿命定义为燃料电池总成本(包括制造成本和使用过程中燃料与附属设备消耗成本)除以使用时间得到的平均使用成本最小时的燃料电池工作时间。燃料电池到达其经济寿命后，更换膜-电极组件，进入第2轮寿命循环，分析表明，第2轮寿命循环的平均成本有所降低，经济寿命相应缩短。最后分析了氢气价格和电池衰减率等因素对燃料电池经济寿命的影响。

PEM燃料电池；寿命评价；成本；经济寿命；第2寿命周期

前言

质子交换膜燃料电池具有效率高、启动快、能量密度大、噪声低和零污染等优点，被认为是最有可能替代内燃机的下一代车用动力装置之一。但是目前仍有很多问题制约其商业化进程，其中寿命和成本是其中两个主要因素。

目前质子交换膜燃料电池作为车用能源时寿命只有2 500～3 000h[1]，而作为固定电源时的寿命可超过30 000h[2]。为解决燃料电池的寿命问题，很多研究者进行了燃料电池寿命影响因素、燃料电池耐久性和燃料电池寿命预测方法的研究，文献[3]中研究了含有汞蒸气杂质的氢气对PEM燃料电池寿命的影响。文献[4]中进行了燃料电池在变载情况下的耐久性和寿命测试，指出燃料电池的寿命主要取决于膜的种类。文献[5]中通过燃料电池车的实测数据提出了快速预测燃料电池寿命的方法。文献[6]中通过加速和启停衰减试验给出了寿命预测的方法。文献[7]中通过电化学阻抗谱和极化曲线的测量估测燃料电池已经工作寿命和预测剩余寿命，误差为2‰。文献[8]中通过使用聚合物加固燃料电池的催化剂层来延缓催化剂层的流失以延长膜的使用寿命。

现在对于燃料电池寿命的评价有多种方法，没有统一的标准[9]，有两种比较常见。一种侧重于电池工作性能的衰减，与内燃机的寿命定义相似，权衡燃料电池性能与初始性能的差异。但是不同的研究机构使用不同的评估参数，所以最后的评价结果也是参差不齐。评价参数主要有燃料电池最大输出功率、电池堆电压、电流、额定功率和额定工况的最低电压。另外一种是侧重于电池部件材料的衰减，与化工产品的寿命评价类似，从关键部件的衰减来评估，主要是膜-电极组件(membrane-electrode assembly, MEA)。各研究机构对燃料电池寿命没有统一的定义。巴拉德公司指出燃料电池的使用寿命是指电池堆的最大功率到下降到起初的90%所经历的时间。跟内燃机的寿命定义有很大的相似点，都是用始末性能的百分比衡量，不同的是百分比的确定方法。各个研究机构性能衰减百分比的确定方法与其研究水平以及燃料电池的应用要求都有关系。文献[10]中提出燃料电池的使用寿命是指从平均单片电压0.7V开始的输出功率，到该燃料电池的最大功率下降到再也达不到此功率为止所维持的工作时间。平均单片电压0.7V一般定义为燃料电池工作的标准工况，蓄电池的存在使大多数时候车用燃料电池的输出性能都在此附近。这种定义方法保证了标准工况的输出功率，有一定的实际应用价值。美国福特公司的专家主张把燃料电池的寿命定义为从开始到燃料电池在同一工作电流下单片平均电压下降70mV时所经历的时间。

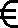
目前燃料电池系统设计思路是追求高性能延长寿命的同时适度地考虑成本。由于燃料电池本身的复杂性和涉及的诸多问题，在燃料电池寿命与成本之间寻求平衡是一项值得研究的课题。本文中首次提出结合成本的PEM燃料电池寿命评价方法—将车用质子交换膜燃料电池经济寿命定义为燃料电池的总成本(包括制造成本及使用成本)除以使用时间得到的平均成本最小时的燃料电池寿命。

1 模型建立

本文的模型建立在以下假设基础上：

(1) 燃料电池在正常使用过程中没有大故障和大修理，保证电压的衰减是一个连续的过程；

(2) 根据大多数燃料电池使用过程中的负载控制模式，假设燃料电池工作在电流控制模式；

(3) 一般燃料电池汽车在同一工况运行时功率波动很小，假设在同一工况下处于恒功率模式；

(4) 燃料电池寿命周期内电压呈线性衰减[5]。

本文中符号说明如下：

C0—单位功率燃料电池堆制造成本，$/kW；

P0—燃料电池堆初始设计功率，kW；

Qtotal—从燃料电池制造过程到使用时间t时电池的总成本，$；

Qstack—燃料电池堆的总制造成本，$；

QH2—燃料电池堆单位使用时间内氢气的消耗成本，$/h；

Qope—燃料电池堆单位使用时间内附件的消耗成本，$/h；

CH2—氢气的价格，$/kg；

Celec—电能价格，$/(kW·h)；

Pidl—怠速时电池功率，kW；

Plow—中低负荷时燃料电池输出功率，kW；

Phea—大负荷时燃料电池输出功率，kW；

tidl—燃料电池使用过程中每小时内怠速时间，h；

tlow—燃料电池使用过程中每小时内中低负荷运行时间，h；

thea—燃料电池使用过程中每小时内大负荷运行时间，h；

U0—燃料电池初始额定电压，V；

I(t)—燃料电池工作过程中t时刻的电流，A；

α—燃料电池使用过程中的电压衰减率，V/h；

λ—燃料电池使用过程中氢气的过量系数；

MH2—氢气的摩尔质量，kg/mol；

F—法拉第常数；

n—电池堆内燃料电池的片数；

z—每个氢气分子参加反应所转移的电子数；

Ut—燃料电池使用过程中任意时刻的电压，V；

η—燃料电池使用过程中氢气的利用率。

1.1 平均成本的计算

燃料电池使用时间为t时，燃料电池总的消耗成本包含燃料电池的制造成本、氢气消耗成本和附属设备消耗成本。

(1)

(1) 燃料电池的制造成本为

Qstack=C0P0

(2)

(2) 燃料电池使用过程中，附属设备的消耗成本包括：增湿水消耗成本Qhum_H2O和冷却水消耗成本Qcold_H2O；空压机、增湿器和各种电子控制器件等的电力消耗Qelec。

Qope=Qhum_H2O+Qcold_H2O+Qelec

(3)

表1展示了主要附属设备的典型费用值。

表1 各类附件消耗的成本[18-19]

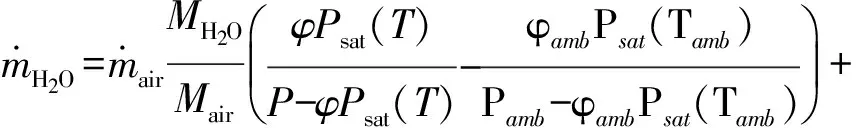
(4)

式中：mH2O，mair和mH2分别指单位时间消耗的水、空气和氢气；MH2O，Mair和MH2分别为水、空气和氢气的摩尔质量；φ和φamb分别为燃料电池入口气体和周围空气的相对湿度；T和Tamb分别为燃料电池入口气体和周围空气的温度；P和Pamb分别为燃料电池入口气体和周围空气的压力。

由式(4)可以看出，在燃料电池固定增湿比，进口温度恒定，压力认为固定不变的情况下，增湿用水量和反应空气和氢气的量成正比。由于在燃料电池工作过程中已经设定过量系数不变，空气的供应量与氧气的消耗量成正比，即也与氢气的消耗量成正比，则

Qhum_H2O=k1QH2

(5)

式中k1为比例常数。

冷却用水的计算可以近似认为燃料电池工作温度恒定，且冷却效果极好，由于电池产生热量与反应的剧烈程度成正比，所以近似认为冷却用水量与电池的氢气消耗量成正比。

Qcold_H2O=k2QH2

(6)

式中k2为比例常数。

在电池运行过程中，空压机、水泵和电子控制系统等辅助系统消耗的电能占电池产生电能的百分比为η，在很多已经运行的燃料电池系统中η为22%[10]。所以系统附件每小时的消耗为

Qelec=ηCelec∑P

(7)

式中∑P为各个控制元件消耗的总功率。

在电池运行过程中产生的电能又与氢气的消耗量成正比，所以附件系统消耗的电能也与氢气的消耗成正比，即

Qelec=k3QH2

(8)

式中k3为比例常数。

由式(5)、式(6)和式(8)得出燃料电池运行过程中燃料电池总的附件消耗为

Qope=kopeQH2

(9)

其中kope=k1+k2+k3

(3) 在车用燃料电池中，电池主要工况有启停、怠速、大幅变载、中低负荷运行和大负荷运行5种。文献[5]中通过在燃料电池公交车采集的运行数据进行循环谱分析发现，燃料电池公交车每小时进行56次加载，启停0.99次，怠速工况13min,大负荷运行14min，在这里假设除怠速工况和大负荷运行外其余工况为中低负荷运行工况，加载和启停的时间与运行过程的整个时间历程相比，可以忽略不计，只对电池的衰减产生影响，则中低负荷运行33min。当然不同的汽车在不同的运行环境下各个工况运行功率Pi及运行时间ti取值不同。

任意时刻的电压为

Ut=U0-αt

(10)

式中t为燃料电池使用时间。

每小时氢气消耗量为

(11)

每小时氢气消耗成本为

QH2=CH2mH2

(12)

将各个表达式代入，使用时间为t时，燃料电池系统的总消耗成本为

(13)

(14)

电池使用的经济寿命t*是包括制造成本在内的电池的所有寿命历程中氢气及附件取得最小值时对应的使用时间。只有在最佳寿命t*时电池的平均使用成本是最低的，当使用时间大于或者小于t*时，其平均成本都会大于t*对应的最低平均成本Qmin。

1.2 燃料电池第2轮寿命周期

当电池使用到最经济寿命后，可以采用更换燃料电池内部易损件继续使用。在质子交换膜燃料电池内部制约其寿命的是电池的MEA。

假设MEA组件成本是电池堆制造成本的r倍(燃料电池量产时r值约为65%，参见表2)，则第2轮使用周期的电池堆制造成本为

Qstack,2=rC0P0

(15)

表2 模型计算参数的选取

假设更换后的MEA组件与第1周期所用的相同，则电压U0具有相同的衰减率α。

则第2使用周期单位时间氢气消耗成本为

(16)

其中t2=t-t*

(17)

式中t2为在第2个使用周期的使用时间，h。

同样，第2周期包括制造成本、氢气消耗和附件消耗的平均成本，即

(18)

2 模型的分析与计算

利用以上公式(式中参数的取值见表2)，采用Matlab对模型计算，得到电池平均使用成本随使用时间变化曲线，如图1所示。

由图可见，当电池使用时间t取经济寿命为t*=5 581h时取平均成本的最小值是72.051$/h。这个寿命结果满足了车用燃料电池寿命5 000h，达到商用要求[10]。当电池的使用时间大于或者小于该时间都会使电池的平均成本增加，对用户来说是不划算的。所以最经济的手段是在电池使用到经济寿命t*时对电池内部影响其衰减率的部件，例如MEA等进行更换。

由图可见，经过更换MEA进行第2轮寿命周期，燃料电池的经济寿命缩短了，不需要很长的时间就可以达到平均成本的最小值，并且平均成本有所降低。

2.1 氢气价格的影响

氢气是PEM燃料电池使用过程中的主要燃料消耗，所以氢气价格对电池的平均成本和经济寿命有很大的影响，如图3所示。从图3中可以看出，氢气的价格越低，单位时间的消耗成本越低。当氢气制造问题很好解决后，降低氢气的使用成本就能很好降低燃料电池的平均使用成本从而推动燃料电池的市场化。从图3中也可以看出，随氢气的价格降低，燃料电池的经济寿命延长，可以解释为氢气价格的降低，日常的消耗成本对燃料电池总平均成本的影响减小，使电池的制造成本在电池总平均成本中所占的比例增大，而一个确定的电池堆的制造成本是固定的，所以使用的时间越长，单位时间平摊的制造成本越低。图4是美国DOE对电解水制氢成本现状的调查和未来成本的预测柱状图，可见降低氢气价格关键在生产规模和用户群体的大小。

2.2 电池堆单位功率制造成本的影响

电池堆单位功率制造成本越高，其总的平均成本越高，经济寿命越长，如图5所示。当电池堆单位功率制造成本越高时，相同功率电池总成本越高，与电池日常使用中的消耗成本相比，电堆制造成本所占的比例越大，需要较长的使用时间去平摊其制造成本。表3是美国DOE对燃料电池制造成本的调查及预测表。由表中可知，只有实现大规模的生产才能实现制造成本的持续降低。当然要实现更低的目标成本还要加强研究新材料、新技术以降低膜及催化剂层等关键部件成本所占的比例。

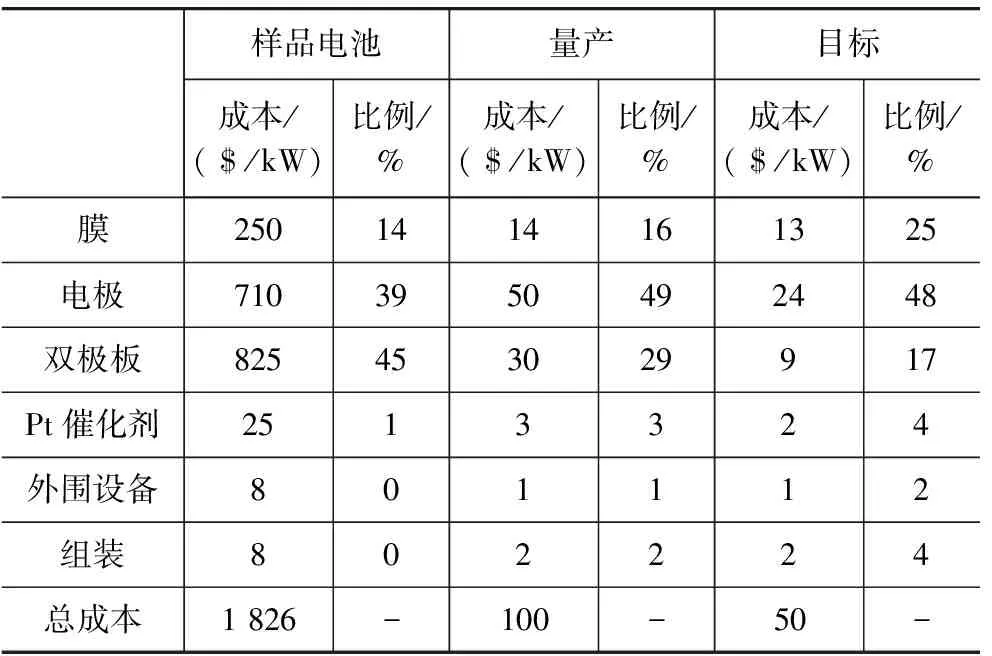
表3 PEM燃料电池堆各个部件制造成本及其所占的成本比例(DOE)

2.3 燃料电池电压衰减率的影响

电池衰减率越大，使用过程中平均成本越高，经济寿命越短，如图6所示。当电池衰减率很大时，随着电池的使用性能和效率的快速下降，日常消耗所占的比例快速增长，很快就能达到其经济寿命，而继续使用时会使平均成本快速增加。电池制造过程中膜-电极组件和流场的良好设计与匹配、使用过程中良好的热管理与水管理、变载速度的合理控制、正确地保护电池使其以舒服的方式工作等等，都能有效减小电池的衰减率，降低电池的平均成本，以延长其经济寿命。

2.4 电池堆设计功率的影响

不同电池堆功率下电池堆使用成本随时间而变化的曲线如图7所示。电堆设计功率越小，单位时间消耗的氢气少，制造成本低，平均成本也低。但电池的经济寿命变化不大。

3 结论

在结合成本的评价即燃料电池经济寿命的评价方法中，综合考虑系统的制造成本和电池在不同的工况使用过程中的费用消耗。经济寿命可以用来评价燃料电池的使用寿命，其更重要的意义在于可以用来表征电池设计过程中顾及成本最佳的情况下所选取材料的耐久性。本文中给出的平均使用成本Q(t)表达式可用于燃料电池最佳设计寿命预测、设计过程中材料耐久性和制造成本及MEA参数的匹配选择。燃料电池达到经济寿命后进行更换MEA等易损件，进入第2轮寿命周期，经分析发现其第2周期的经济寿命缩短，平均成本有所降低。最后分析了经济寿命的影响因素，结果表明，氢气的价格越高，电池堆的制造成本越低，电池的衰减率越大，则经济寿命越短；但其初始设计功率对经济寿命的影响不大。

[1] Kocha S S. Fuel Cells[M]. Springer,2013.

[2] Verhage A J, Coolegem J F, Mulder M J, et al. 30,000h Operation of a 70kW Stationary PEM Fuel Cell System Using Hydrogen from a Chlorine Factory[J]. International Journal of Hydrogen Energy,2013,38(11):4714-4124.

[3] Bouzek Karel, Paidar Martin, Mališ Jakub, et al. Influence of Hydrogen Contamination by Mercury on the Lifetime of the PEM-type Fuel Cell[J]. Electrochimica Acta,2010,56(2):889-895.

[4] Marrony M,Barrera R, Quenet S, et al. Durability Study and Lifetime Prediction of Baseline Proton Exchange Membrane Fuel Cell Under Severe Operating Conditions[J]. Journal of Power Sources,2008,182(2):469-475.

[5] Pei Pucheng, Chang Qianfei, Tang Tian. A Quick Evaluating Method for Automotive Fuel Cell Lifetime[J]. International Journal of Hydrogen Energy,2008,33(14):3829-3836.

[6] Bae Suk Joo, Kim Seong-Joon, Park Jong In, et al. Lifetime Prediction of a Polymer Electrolyte Membrane Fuel Cell via an Accelerated Startup-shutdown Cycle Test[J]. International Journal of Hydrogen Energy,2012,37(12):9775-9781.

[7] Onanena R, Oukhellou L, Candusso D, et al. Fuel Cells Static and Dynamic Characterizations as Tools for the Estimation of Their Ageing Time[J]. International Journal of Hydrogen Energy,2011,36(2):1730-1739.

[8] Cheng Niancai, Mu Shichun, Pan Mu, et al. Improved Lifetime of PEM Fuel Cell Catalysts Through Polymer Stabilization[J]. Electrochemistry Communications,2009,11(8):1610-1614.

[9] 周苏,纪光霁,陈凤祥,等.车用质子交换膜燃料电池系统技术评估与分析[J].汽车工程,2010,32(9):750-756.

[10] Larminie J, Dicks A. Fuel Cell System Explained[M]. John Wiley & Sons,2000.

[11] Marquis J, Coppens M O, et al. Achieving Ultra-high Platinum Utilization via Optimization of PEM Fuel Cell Cathode Catalyst Layer Microstructure[J]. Chemical Engineering Science,2013,102(0):151-162.

[12] Avasarala Bharat, HaldarPradeep, et al. Durability and Degradation Mechanism of Titanium Nitride Based Electrocatalysts for PEM (Proton Exchange Membrane) Fuel Cell Applications[J]. Energy,2013,57:545-553.

[13] Nikolic Vladimir M, Zugic Dragana L, Perovic Ivana M, et al. Investigation of Tungsten Carbide Supported Pd or Pt as Anode Catalysts for PEM Fuel Cells[J]. International Journal of Hydrogen Energy,2013,38(26):11340-11345.

[14] Heinzel A, Mahlendorf F, Niemzig O, et al. Injection Moulded Low Cost Bipolar Plates for PEM Fuel Cells[J]. Journal of Power Sources,2004,131(1-2):35-40.

[15] Mayer Thomas,Kreyenberg Danny, Wind Jörg, et al. Feasibility Study of 2020 Target Costs for PEM Fuel Cells and Lithium-ion Batteries: A Two-factor Experience Curve Approach[J]. International Journal of Hydrogen Energy,2012,37(19):14463-14474.

[16] Schoots K, Kramer G J, van der Zwaan B C C. Technology Learning for Fuel Cells: An Assessment of Past and Potential Cost Reductions[J]. Energy Policy,2010,38(6):2887-2897.

[17] Staffell I, Green R J. Estimating Future Prices for Stationary Fuel Cells with Empirically Derived Experience Curves[J]. International Journal of Hydrogen Energy,2009,34(14):5617-5628.

[18] Barbir F, Gómez T. Efficiency and Economics of Proton Exchange Membrane (PEM) Fuel Cells[J]. International Journal of Hydrogen Energy,1997,22(10-11):1027-1037.

[19] Kazim Ayoub. Exergoeconomic Analysis of a PEM Fuel Cell at Various Operating Conditions[J]. Energy Conversion and Management,2005,46(7-8):1073-1081.

[20] Barbir Frano. PEM Fuel Cells: Theory and Practice[M]. Elsevier Academic Press: Burlington,2005.

[21] 周苏,纪光霁,马天才,等.车用质子交换膜燃料电池系统技术现状[J].汽车工程,2009,31(6):489-495.

A Study on the Economical Lifetime of the ProtonExchange Membrane Fuel Cells for Vehicles

Chen Huicui & Pei Pucheng

TsinghuaUniversity,StateKeyLabofAutomotiveSafetyandEnergy,Beijing100084

In this paper, a service life evaluation method for vehicular PEM fuel cell --- fuel cell economical lifetime is proposed with its math model set up. Fuel cell economical lifetime is defined as the service time of fuel cell when its average service cost (total cost, i.e. the manufacture cost plus the consumption costs of fuel and accessory devices divided by service time) is minimum. When fuel cell reaches its economical lifetime, its membrane-electrode assembly is renewed and the fuel cell enters its second life cycle. The results of analysis indicate that both the average service cost and corresponding economical lifetime in second life cycle is slightly less than those in first life cycle. Finally the effects of factors including hydrogen price and fuel cell decay rate on the economical lifetime of fuel cell are analyzed.

PEM fuel cells; lifetime evaluation; cost; economical lifetime; second life cycle

*国家自然科学基金(21376138)、国家973计划项目(2012CB215505)和国家863计划项目(2012AA1106012,2012AA053402)资助。

原稿收到日期为2014年1月8日。