分布式电驱动车辆纵-横-垂向力协同控制*
2015-04-12罗禹贡戴一凡褚文博李克强
曹 坤,罗禹贡,戴一凡,褚文博,陈 龙,李克强
(清华大学,汽车安全与节能国家重点实验室,北京 100084)
2015170
分布式电驱动车辆纵-横-垂向力协同控制*
曹 坤,罗禹贡,戴一凡,褚文博,陈 龙,李克强
(清华大学,汽车安全与节能国家重点实验室,北京 100084)
针对现有研究多采用经验工况划分、主动悬架力简单分配等轮胎力解耦控制方法,难以实现车辆性能最优化的问题,提出了分层式轮胎纵-横-垂向力协同优化控制系统,在制定上层行驶期望目标和下层执行控制策略的同时,重点研究了中层轮胎纵-横-垂向力优化分配。建立了融合轮胎负荷率和垂向力动态系数的统一优化目标函数,综合考虑了车辆行驶期望目标、轮胎附着极限和执行器特性等约束条件,最终解决了轮胎纵、横、垂向力的协同优化控制难题。基于Matlab/Simulink和CarSim的联合仿真结果表明,提出的分层协同控制系统能同时有效控制车辆行驶姿态和改善车辆操纵稳定性能。
分布式电动车辆;纵-横-垂向力分配;协同控制
前言
随着汽车技术的进步,多种底盘电控技术得到了广泛的研究和应用。牵引力控制系统、主动转向系统和主动悬架系统等分别对轮胎纵向、横向和垂向力进行优化分配和主动控制,提升车辆的综合性能[1]。由于车辆各向运动和轮胎各向力具有复杂的耦合特性,采用不同的底盘电控系统分别对轮胎力进行单一方面的控制势必导致控制目标和执行效果的冲突,因此对车辆纵向、横向和垂向力进行协同控制的底盘一体化技术得到了广泛研究[2]。
文献[3]中讨论了制动和主动悬架的协同控制,提出主动悬架力随制动力矩相应变化以减小制动距离。文献[4]中则从提高车辆横向稳定和侧倾安全的角度研究了电驱动车辆制动力和主动悬架力的协同控制。文献[5]中讨论了基于侧倾指数的线控转向与主动侧倾力矩的协同控制。文献[6]中则提出在轮胎侧向力达到饱和的工况下,结合独立转向和增大主动悬架力提高侧向力极限。文献[7]中研究了轮胎纵向和横向力协同控制,提出基于轮胎负荷率优化的轮胎纵向和横向力分配方法。文献[8]中讨论了独立驱动、主动前轮转向和主动悬架的协同控制,但未考虑主动悬架力的优化分配。文献[9]中则针对不同行驶工况,采用不同的制动/转向/悬架控制组合进行协调控制。文献[10]中提出以载荷转移分配调节各轮抓地力,再以稳定性指数协调制动与转向的协同控制方法,但该方法将垂向力分配与纵向和横向协调直接解耦,可能导致部分车轮附着情况恶化。
不难发现,上述底盘一体化的研究皆为对轮胎纵向、横向和垂向力的二者或三者进行协同控制。其中,基于优化分配的轮胎纵向和横向力综合控制实现了轮胎力的耦合控制;而涉及轮胎垂向力控制的研究则大多采用经验工况划分和简单分配等人为解耦的方法,难以最大限度地提升车辆性能。为此,必须建立统一的轮胎纵向、横向和垂向力协同优化方法。本文中以具有四轮独立驱动/转向和主动悬架系统的分布式电驱动车辆为研究对象,提出分层式轮胎纵-横-垂向力协同优化控制系统,对上层行驶期望目标策略制定、对中层纵-横-垂向力协同优化方法和下层执行控制策略进行了详细研究,并通过Matlab/Simulink和CarSim联合仿真系统对所提控制系统进行了验证和评价。
1 分层式轮胎纵-横-垂向力协同优化控制系统
本文中提出的分层式轮胎纵-横-垂向力协同优化控制系统结构框图如图1所示。
在该分层控制系统中,上层根据车辆状态参数判断车辆行驶期望并确定期望合力与力矩;中层建立目标函数和约束条件,将期望合力和力矩协同优化分配为各轮纵向、横向和垂向力;下层对电机驱动系统、前/后轮主动转向系统和主动悬架系统进行精确控制,实现所分配的最优轮胎力。
1.1 上层:车辆行驶期望目标策略的制定
车辆纵向加速度通常可描述为加速踏板位置和纵向车速的函数,见式(1)。为实现这一期望加速度,车辆期望纵向合力可由式(2)得到。
ax,des=f(α,vx)
(1)
Fx,des=max,des
(2)
式中:ax,des为期望纵向加速度;α为加速踏板行程;vx为纵向车速;Fx,des为期望纵向合力;m为整车质量。
车辆转向时的期望横向合力为
(3)
式中:Fy,des为期望横向合力;R为转向半径。
由于行驶过程中车辆实际位置与理想轨迹往往存在偏差(图2),预期转向半径须根据车辆横摆姿态动态调整,动态预期转向半径为
(4)
式中:R0为理想轨迹的曲率半径;L为预瞄行驶距离;df和dr为车辆前、后轴中心点与理想轨迹的距离;l为车辆轴距;lf和lr为前、后轴中心点至质心的距离。
为实现车辆平稳转向,还须确定车辆预期横摆角速度。根据具有前、后轮转向的2自由度车辆模型,车辆横摆角满足:
(5)
式中:Ψ为轴距l对应的横摆角;δf和δr分别为前、后轮转向角;αf和αr分别为前、后轮侧偏角;γ为车辆实际横摆角速度。
由式(4)和式(5),结合式(36)的轮胎侧偏角目标值,则车辆预期横摆角速度为
(6)
式中:αf,des和αr,des分别为前、后轮轮胎侧偏角目标值;γdes为车辆预期横摆角速度。
为使车辆的实际横摆角速度跟随期望横摆角速度变化,并抑制因加速产生的车身俯仰角和侧倾角,采用PID方法确定期望横摆力矩、期望侧倾力矩和期望俯仰力矩:
Mz,des=(KP1+KI1/s+KD1·s)(γdes-γ)
(7)
Mx,des=(KP2+KI2/s+KD2·s)(ρdes-ρ)
(8)
My,des=(KP3+KI3/s+KD3·s)(θdes-θ)
(9)
式中:Mz,des,Mx,des和My,des分别为期望横摆力矩、期望侧倾力矩和期望俯仰力矩;KP1,KP2和KP3为比例参数;KI1,KI2和KI3为积分参数;KD1,KD2和KD3为微分参数;s为拉普拉斯算子;ρdes为期望侧倾角,ρdes=0;θdes为期望俯仰角,θdes=0。
此外,为避免车身出现持续的垂向加速度从而影响乘坐舒适性,造成悬架位移过大,各轮垂向力之和应与车重相等,即
Fz,des=mg
(10)
式中Fz,des为车辆期望垂向合力。
1.2 中层:轮胎力分配
车辆行驶期望合力与力矩须靠各轮的纵向、横向和垂向力来实现。为此,中层解决期望合力与力矩的分配问题,主要包括约束条件的确定、目标函数的选取和优化求解算法的设计。
1.2.1 约束条件
各轮纵向、横向和垂向力所需满足的约束条件为
Fx,des=Fxfl+Fxfr+Fxrl+Fxrr
(11)
Fy,des=Fyfl+Fyfr+Fyrl+Fyrr
(12)
Fz,des=Fzfl+Fzfr+Fzrl+Fzrr
(13)
Mx,des=0.5tf(Fzfl-Fzfr)+0.5tr(Fzrl-Fzrr)
(14)
My,des=-lf(Fzfl+Fzfr)+lr(Fzrl+Fzrr)
(15)
Mz,des=lf(Fyfl+Fyfr)-lr(Fyrl+Fyrr)+
0.5tf(-Fxfl+Fxfr)+0.5tr(-Fxrl+Fxrr)
(16)
Fyfl·Fzfr-Fyfr·Fzfl=0
(17)
Fyrl·Fzrr-Fzrl·Fyrr=0
(18)
(19)
-Ti,max/r≤Fxi≤Ti,max/r
(20)
-Fy,max≤Fyi≤Fy,max
(21)
-kxi,max/r≤ΔFxi/Δt≤kxi,max/r
(22)
-kyi,max≤ΔFyi/Δt≤kyi,max
(23)
-kzi,max≤ΔFzi/Δt≤kzi,max
(24)
Fzi≥0
(25)
其中,各轮纵向、横向和垂向力须提供车辆行驶期望所需合力与力矩,应满足约束式(11)~式(16);考虑到高速行驶时四轮转向角差别不宜过大,即同轴左/右轮转向角应近似相等,且侧偏角较小时轮胎横向力与垂向力近似为线性关系,同轴左/右轮的横向力与垂向力应满足约束式(17)和式(18);由于轮胎与地面间附着条件限制,各轮纵向、横向和垂向力应满足约束式(19);各轮纵向、横向和垂向力不能超过执行器执行范围,因此轮胎力最大值和轮胎力最大变化率应满足约束式(20)~式(24);此外,各轮垂向力均应为正值,即满足约束式(25)。
式(11)~式(25)中:下标i分别代表fl,fr,rl和rr,对应左前轮、右前轮、左后轮和右后轮;Fxi,Fyi和Fzi分别为各轮纵向、横向和垂向力;tf,tr为前、后轴轮距;μi为各轮与路面间的摩擦因数;Ti,max为电机最大转矩;Fy,max为轮胎最大横向力;r为轮胎有效半径;Δt为时间步长;ΔFxi,ΔFyi和ΔFzi分别为Δt内轮胎纵向力、横向力和垂向力变化量;kxi,max,kyi,max和kzi,max分别为电机转矩最大变化率、轮胎横向力最大变化率和轮胎垂向力的最大变化率。
1.2.2 目标函数
满足式(11)~式(25)约束条件的轮胎力分配值有无穷多组,因此必须设计合理的优化目标函数作为力分配效果的评价指标,求得唯一的最优解。
本文中结合式(26)定义的轮胎负荷率和式(27)定义的轮胎垂向力动态系数,采用式(28)所示目标函数对轮胎纵向、横向和垂向力优化分配进行评价。
(26)
εi=Fzi,0/Fzi
(27)
(28)
式中:γi为各轮轮胎负荷率;εi为轮胎垂向力动态系数;Fzi,0表示各轮静载;Var表示计算方差;E表示平均值;w1和w2为权重系数。
须指出,在各轮垂向力作为已知量不能被自由分配的情形下,最小化轮胎负荷率方差与均值加权和可实现轮胎纵向、横向力的优化分配[11]。但在本文中垂向力为待分配的自由变量,仅优化轮胎负荷率可能出现负荷率较优但垂向力大小相差极大的分配结果。为避免由此导致主动悬架控制产生较大的悬架动位移,影响车辆稳定,各轮垂向力与其静载之差不宜过大。为此,在目标函数中额外考虑最小化垂向力动态系数方差,使各轮垂向力与其静载较为接近,避免悬架动位移过大,同时也使得主动垂向力控制量较小。
结合负荷率和垂向力动态系数的优化,式(28)目标函数能综合反映车辆操纵稳定性、纵-横-垂向力动态耦合特性和悬架动位移限制特性,可用于评价各轮纵向、横向和垂向力的优化分配效果。
1.2.3 优化求解
式(11)~式(25)约束条件和式(28)目标函数构成完整的轮胎力优化分配问题。在初始阶段,暂不考虑轮胎力变化率约束,对不等式约束引入松弛变量,对目标函数构造障碍函数项,该问题的统一数学模型为
(29)
式中:x=[FxiFyiFzi]T表示各轮纵、横、垂向力组成的12×1列向量;f(x)为目标函数,见式(28);g和h分别为1.2.1节所述约束条件中等式约束和不等式约束的表达式;k和j分别对应第k个不等式约束和第j个等式约束;sk为对应于第k个不等式约束的松弛变量;μ为障碍函数的罚因子变量,其值为正且在求解过程中逐渐趋近于零。
式(29)的拉格朗日函数见式(30),并对其应用约束优化问题的KKT条件,得式(31)。
(30)
(31)
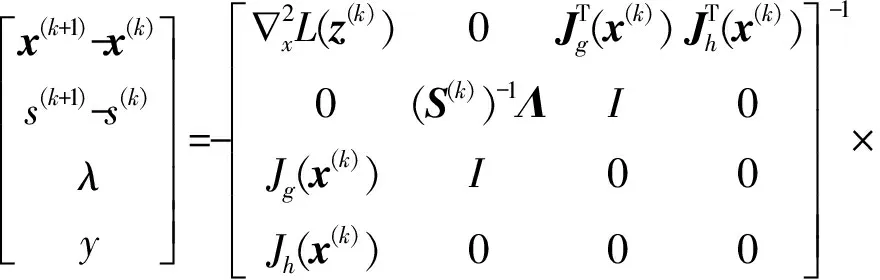
(32)

由式(11)~式(16)可知,轮胎力最优解随期望纵/横向加速度、期望横摆/侧倾/俯仰力矩的变化而变化。在连续优化过程中,利用前一时刻迭代所得最优解,可将当前时刻最优解的可行域限定在其相应的邻域内,即
xopt(t)-ξ(ΔEm)≤xopt(t+Δt)≤xopt(t)+ξ(ΔEm)
(33)式中:xopt=[Fxi,opt,Fyi,opt,Fzi,opt]T为最优解;Fxi,opt,Fyi,opt和Fzi,opt分别为纵向、横向和垂向力最优值向量;E=[ax,des,ay,des,Mx,des,My,des,Mz,des]T为期望值向量;ΔEm为时间步长Δt内E的最大变化值;xopt(t)和xopt(t+Δt)分别为在t和t+Δt时刻的各轮纵向、横向和垂向力最优解;ξ(ΔEm)为根据ΔEm确定的邻域半径。
将式(33)作为新增约束加入迭代过程,可将搜索空间限定在前一时刻最优解附近,从而避免可行域宽泛引起迭代发散,满足轮胎力变化率约束,获得可实际执行的轮胎力最优解。
1.3 执行控制
各轮的期望驱动转矩为
Twi=Fxi,optr
(34)
为实现各轮垂向力最优分配值,在估计各轮实际垂向力的基础上利用主动悬架力进行差值补偿控制。各轮所需的主动悬架力为
(35)

为实现轮胎横向力最优分配值,本文中采用基于Dugoff模型的解析式轮胎逆模型[11],将横向力分配值转化为轮胎侧偏角目标值:
(36)
式中:Cλ为轮胎滑移刚度;Cα为轮胎侧偏刚度。
利用二自由度车辆模型及式(4)和式(6),则各轮期望转向角为
(37)
2 仿真试验
本文中基于Matlab/Simulink和CarSim联合仿真平台,对提出的纵-横-垂向力协同控制方法进行了仿真验证。仿真中所选分布式电动车辆的主要动力学参数如表1所示。
为比较控制效果,将本文中控制方法与当前研究中其他3种控制方法进行对比。其中,方法1中四轮转矩平均分配,各轮转角由式(37)右侧第3项确定,无目标侧偏角反馈;方法2中基于负荷率方差与均值加权最小化,协同控制纵横向力[11];方法3中在纵横向力协同控制基础上,根据期望俯仰/侧倾力矩在各轮间简单平均分配主动悬架力[8];方法4中为本文中提出的纵-横-垂向力协同控制方法。
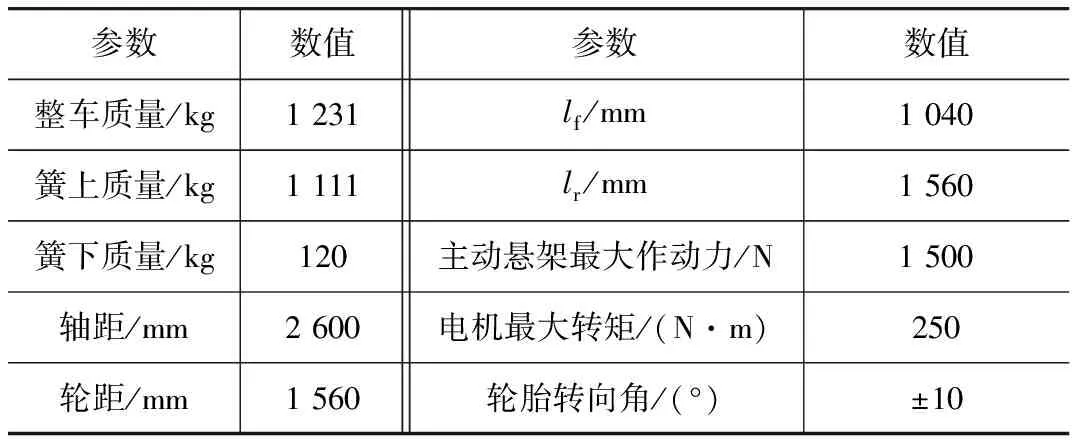
表1 分布式电动车辆主要动力学参数
为对控制系统进行充分验证,分别在直线加速、匀速/加速回转、匀速/加速双移线等多种工况下进行了仿真研究。限于篇幅,本文中仅给出一组髙附路面下加速双移线工况的仿真结果,如图3~图6所示。
由图3可知,方法1和方法2未实施主动悬架力控制,在纵向和横向加速过程中车身俯仰角峰值均达2.6°,车身侧倾角峰值分别达6.9°和6.5°。方法3采取了主动悬架力控制,将车身俯仰角和侧倾角峰值控制为0.12°和0.5°,改善了车辆行驶姿态。方法4采用协同控制方法,将车身俯仰角和侧倾角峰值控制为0.1°和0.4°。
由图4(a)可知,方法4中质心侧偏角大幅改善,其最大值为0.5°,其他3种方法分别为2.4°,0.9°和1.4°。由图4(b)可知,相比其他3种方法,方法4中横摆角速度更平稳且在第6s后明显较小;第6.5s附近,横摆角速度峰值为12.2°/s,其他3种方法依次为14.0°/s,14.5°/s和13.9°/s。因此,方法4对质心侧偏角和横摆角速度都有明显改善。
由图5可知:方法1未优化分配轮胎力,轮胎负荷率最高,最大负荷率为84%,平均负荷率为29%;方法2综合优化轮胎纵向和横向力,大幅降低了轮胎负荷率,最大负荷率为68%,平均负荷率为27%;方法3简单分配垂向力,使轮胎负荷率较方法2恶化,最大负荷率为79%,平均负荷率为28%;方法4综合优化轮胎纵向、横向和垂向力,大幅改善了方法3对轮胎负荷率的恶化,最大负荷率为71%,平均负荷率为24%。
由图6可知:方法1和方法2中垂向力最大值分别为5 173和5 130N,最小值分别为1 015和1 087N;方法3中垂向力波动最大,最大值为5 908N,最小值为292N,且在第7s后趋于发散,可能导致控制失效和车辆失稳;方法4中垂向力变化范围较小,最大值为4 846N,最小值为1 746N,且与各轮静载更为接近,相应悬架动位移较小,利于车辆稳定。
由图3~图6可知,由于采取轮胎纵向、横向和垂向力协同控制,方法4基本消除了由加速运动引起的车身俯仰角和侧倾角,明显降低了质心侧偏角和横摆角速度,同时改善了现有轮胎纵向、横向和垂向力集成控制方法对各轮负荷率的恶化,减小了主动悬架力控制导致的悬架动位移,比现有研究方法更利于车辆稳定。
3 结论
本文中提出了分层式轮胎纵-横-垂向力协同优化控制系统,并重点研究了纵-横-垂向力协同优化方法,通过联合仿真系统对控制系统进行了验证,得到如下结论:
(1) 提出的分层式轮胎纵-横-垂向力协同优化控制系统,较现有研究具有显著优势,在改善车辆行驶姿态的同时,增强了车辆操纵稳定性能;
(2) 提出了结合约束优化和可行域规划,求解具有多个非线性约束和非凸特性的轮胎纵-横-垂向力优化问题的方法;
(3) 提出的融合轮胎负荷率和垂向力动态系数的优化目标函数,能综合反映车辆操纵稳定性、纵-横-垂向力动态耦合特性和悬架动位移限制特性,解决了轮胎纵-横-垂向力优化分配难题。
本文中主要针对轮胎纵-横-垂向力优化分配及控制问题进行初步探讨,在传感信息获取、算法实时性及应对路况变化等方面尚未作重点研究。后续将从改进优化算法和约束条件处理方式等方面寻找提高算法计算效率的途径,针对路面附着系数变化时控制方法对车辆操控性能的控制响应合理设计执行器控制调节策略,以改善控制算法的实时性和对路况变化的适应性,从而提高算法实车应用的可行性。
[1] Wallentowitz H. Scope for the Integration of Powertrain and Chassis Control Systems: Traction Control—All-Wheel Drive—Active Suspension[R]. SAE International,1999.
[2] Yu F, Li D, Crolla D A. Integrated Vehicle Dynamics Control-State-of-the Art Review[C]. IEEE Vehicle Power and Propulsion Conference (VPPC),2008.
[3] Alleyne A. Improved Vehicle Performance Using Combined Suspension and Braking Forces[J]. Vehicle System Dynamics,1997,27:235-265.
[4] Yoon J, Yim S, Cho W, et al. Design of an Unified Chassis Controller for Rollover Prevention, Maneuverability and Lateral Stability[J]. Vehicle System Dynamics,2010,48(11).
[5] Rajamani R, Piyabongkarn D. New Paradigms for the Integration of Yaw Stability and Rollover Prevention Functions in Vehicle Stability Control[J]. IEEE Transactions on Intelligent Transportation System,2012,14(1):5046-5051.
[6] Shen X, Yu F. Investigation on Integrated Vehicle Chassis Control Based on Vertical and Lateral Tyre Behaviour Correlativity[J]. Vehicle System Dynamics,2006,44:506-519.
[7] Mokhiamar O, Abe M. How the Four Wheels Should Share Forces in an Optimum Cooperative Chassis Control[J]. Control Engineering Practice,2006,14.
[8] Cho W, Yoon J, Kim J, et al. An Investigation into Unified Chassis Control Scheme for Optimised Vehicle Stability and Manoeuvrability[J]. Vehicle System Dynamics,2008,46(s):87-105.
[9] Lu S, Li Y, Choi S, et al. Integrated Control on MR Vehicle Suspension System Associated with Braking and Steering Control[J]. Vehicle System Dynamics,49(1-2):361-380.
[10] Fergani S, Sename O, Dugard L. A New LPV/H∞ Global Chassis Control Through Load Transfer Distribution and Vehicle Stability Monitoring[C]. The 5th Symposium on System Structure and Control, Grenoble: France(2013).
[11] Luo Y, Cao K, Dai Y, et al. A Novel Hierarchical Global Chassis Control System for Distributed Electric Vehicles[J]. SAE International Journal of Passenger Cars-Electronic and Electrical Systems,2014,7(2).
Collaborative Control of Longitudinal/Lateral/VerticalTire Forces for Distributed Electric Vehicles
Cao Kun, Luo Yugong, Dai Yifan, Chu Wenbo, Chen Long & Li Keqiang
TsinghuaUniversity,StateKeyLaboratoryofAutomotiveSafetyandEnergy,Beijing100084
In view of that the most of existing researches adopting tire force decoupling control method, including the empirical partition of working conditions and the simple distribution of active suspension forces, are difficult to achieve the optimization of vehicle performances, a hierarchical collaborative optimization control system for longitudinal, lateral and vertical tire forces is proposed. While in working out the expected driving objective in upper layer and actuating control strategy in lower layer, the collaborative allocation for longitudinal, lateral and vertical tire forces in middle layer is emphatically investigated. Then a universal optimization objective function combining both tire loading ratios and dynamic vertical force coefficient is developed, with the constraint conditions including the expected driving objective of vehicle, the adhesion limit of tires and the characteristics of actuator concurrently considered. Finally the difficult issue of collaborative optimization control for longitudinal, lateral and vertical tire forces is resolved. The results of co-simulation with Matlab/Simulink and CarSim show that the layered collaborative optimization control system proposed can concurrently control the driving attitude effectively and improve the handling stability of vehicle.
distributed electric vehicle; longitudinal/lateral/vertical force distribution; collaborative control
*国家重点基础研究发展计划(2011CB711204)资助。
原稿收到日期为2013年9月27日,修改稿收到日期为2014年5月6日。
