基于竞争风险的燃料电池发动机多失效模式统计相关性分析*
2015-04-12郑松林刘新田冯金芝
陈 铁,郑松林,2,刘新田,冯金芝,2
(1.上海理工大学机械工程学院,上海 200093;2. 机械工业汽车底盘机械零部件强度与可靠性评价重点实验室,上海 200093)
2015047
基于竞争风险的燃料电池发动机多失效模式统计相关性分析*
陈 铁1,郑松林1,2,刘新田1,冯金芝1,2
(1.上海理工大学机械工程学院,上海 200093;2. 机械工业汽车底盘机械零部件强度与可靠性评价重点实验室,上海 200093)
为解决复杂系统多失效模式相关性难以判别与量度的问题,提出一种基于竞争风险理论的多失效模式统计相关性分析模型。采用多元对数正态分布建立系统的联合失效分布,构造基于条件概率的极大似然函数,运用模拟退火算法对极大似然估计值进行优化求解。在大样本条件下,凭借Fisher信息矩阵获得极大似然估计量的渐近协方差矩阵,并采用Delta方法推导出相关矩阵的方差。建立相关性p值假设检验过程,判别各竞争失效模式间的相关关系与相关程度。通过对燃料电池发动机的故障数据进行分析,验证所建模型的可行性和有效性,为竞争失效系统的可靠性预测和分配提供理论依据,为研究最优维修策略提供技术基础。
燃料电池发动机;竞争失效模式;失效相关性;多元对数正态分布;模拟退火算法;假设检验
前言
许多复杂系统在工作过程中,往往承受着来自外部或者自身的多重载荷冲击。大部分子系统或内部组件在结构与功能上存在着一定程度的关联,当某子系统或组件失效时,可能会诱发其它子系统或组件失效。在竞争风险场合中,发生任何一种失效模式,系统则失效或停止工作,将无法观察到其它失效模式的发生。因此,利用竞争风险理论可以有效地分析系统失效模式的竞争行为,合理地评价系统的可靠性水平。然而,研究多竞争失效模式间的相关性一直是可靠性理论的难题,其中判别失效模式间是否存在相关性以及相关程度如何量度等问题尤为突出[1-2]。
对于竞争失效模式的可靠性问题,国内外学者做了较为深入的研究。其中大多数假设组件的失效模式在统计上相互独立,这样便可分别对每种失效模式进行独立分析,确定出它们的分布类型和可靠性函数。文献[3]中建立了独立假设条件下的竞争失效模型,并给出了对数正态分布的极大似然估计。文献[4]中采用混合分布对独立竞争失效问题加以研究。文献[5]中针对突发失效模式和退化失效模式并存的竞争风险场合进行建模分析,并采用基于期望最大化的极大似然法和伪失效寿命的极大似然法估计模型参数。研究人员针对竞争失效模式的相关性问题也进行了相关探讨。文献[6]中建立了可靠性模型来描述某组件的失效以某特定概率对其它组件产生冲击影响的现象。文献[7]中基于竞争风险理论提出了考虑失效时间相关的条件分布模型。文献[8]中提出了基于功能函数完全相关或完全独立的一般界限理论。文献[9]中提出了二阶窄界限理论来计算两两失效模式间的相关系数,文献[2]和文献[10]在此基础上,提出了一种仅考虑主次失效模式相关系数的计算方法。文献[11]中利用Copula函数建立联合生存函数来描述多种竞争风险之间的相关关系。文献[12]中针对高寿命产品多故障模式失效的可靠性综合预估问题,建立了多故障模式相关性失效的Copula综合可靠性模型。
综合上述研究,如果忽略竞争失效模式间的相关性,常常会导致系统可靠性分析产生误差。然而,关于竞争失效模式相关性判别与量度方面的研究还少见文献报道。因此,本文中重点研究竞争失效模式相关性判别与量度的问题,提出一种基于多元对数正态分布的竞争失效模式相关性统计可靠性模型,采用基于模拟退火的极大似然估计法对模型参数进行优化求解,并建立完整的相关性p值假设检验过程,验证各竞争失效模式间的相关关系与相关程度。目前,该模型暂不考虑任何维修操作。
1 竞争失效模式统计相关性建模
1.1 失效模式竞争风险模型
在经典竞争风险理论中,一般假设系统由K个组件组成,且对应K种不同的失效模式,每一种失效模式的发生都将导致整个系统失效或停止工作。此外,假定系统同一时刻不可能发生两种或两种以上的失效模式。为了方便问题的阐述,每个组件的潜在失效时间用随机变量Dj表示,j=1,2,…,K。系统中所有组件的潜在失效时间用向量D=[D1,…,DK]T表示,系统的实际失效时间用T=min(Dj)表示,对应的失效模式用I=arg(min(Dj))表示,因此,失效模式竞争风险模型的统计量[13]为
(T,I)={min(Dj),arg(min(Dj))}
(1)

1.2 联合失效分布模型
对数正态分布是一种常用的失效时间分布,多元函数是描述随机变量相关性的根本方法,因此,基于多元对数正态分布函数建立潜在失效时间向量D的联合分布模型。该模型不仅可以描述失效模式统计上独立的情况,同时也可以描述失效模式统计上相关的情况。根据多元对数正态分布的性质,其联合概率密度函数[14]表示为
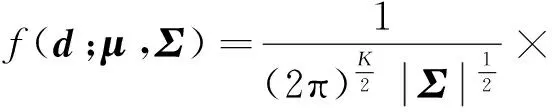
(2)
式中:μ为多元对数正态分布的均值向量;Σ为多元对数正态分布的协方差矩阵。
2 基于条件概率的极大似然估计
2.1 条件似然函数
根据Leibniz法则,对联合概率密度函数进行积分,构造出潜在失效时间向量D的联合生存函数如下:
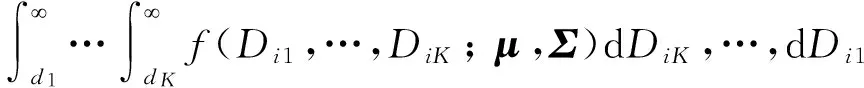
(3)
在ti时刻,第i个系统的组件k失效,其它组件均正常的条件似然函数为
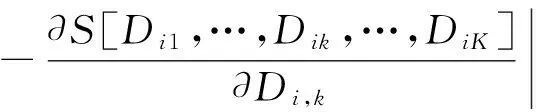
(4)
式中:fk(ti)为组件k潜在失效时间的对数正态边缘分布的概率密度函数;Pr(*)表示在Dik=ti的条件下,事件(Dij≥ti;j≠k,j=1,…,K)发生的概率,即在组件k失效的条件下,系统内其它组件均正常的概率。
综合样本N个观察值,建立完整的条件似然函数如下:
(5)
(6)
(7)
将式(6)和式(7)代入式(5),即可对条件似然函数进行计算。
另外,对于多元对数正态分布的参数估计而言,协方差矩阵Σ需要满足正定性要求,因此,运用矩阵的Cholesky分解法,对协方差矩阵进行三角分解:
Σ=M×MT
(8)
式中M为正定下三角矩阵。
这样便可确保协方差矩阵为实对称正定矩阵。经Cholesky分解后,极大似然估计量可由协方差矩阵Σ转变为矩阵M,记作θ=(μ,M)。
2.2 极大似然估计的模拟退火算法优化
多元对数正态分布的极大似然估计属于多维参数优化问题,采用模拟退火算法可以在随机搜寻过程中使目标函数趋于全局最优,避免陷入局部最优解,设置合适的模拟退火算法的控制参数,有利于获得待估参数的最小无偏估计[16]。算法实施步骤如下:
(1)输入一组服从多元对数正态分布的样本观察值;
(2)设定初始温度T0,极大似然估计量初值θ0,并计算似然函数初值L(θ0);
(3)在极大似然估计量的邻域内随机选取一点θ1,并计算此时似然函数的值L(θ1);
(4)如果Δ=L(θ0)-L(θ1)<0,则接受θ=θ1,否则随机产生u∈U(0,1)。当u (5)如果算法满足终止条件,则输出θ,即得到极大似然估计量的最优解,否则按照冷却策略更新温度T,并返回步骤(3)。 3.1 相关性假设检验模型 两个随机变量的相关关系一般通过相关系数来判别。对于多元分布而言,其相关关系则通过相关矩阵Λ来描述。 (9) Λ=(Λij)K×K (10) 当Λij>0,称失效模式i、j正相关;当Λij<0,称失效模式i、j负相关;当Λij=0,称失效模式i、j不相关。 求出相关矩阵后,需要对其进行假设检验,从而量度出任意两种不同竞争失效模式之间相关程度的显著性。因此,在显著性水平α下,考虑假设检验如下: H0:失效模式i、j在统计上独立; H1:失效模式i、j在统计上相关。 在大样本的情况下,极大似然估计量服从渐近正态分布[17],因此,检验统计量表示为 (11) 随后进行相关性p值检验,p值表示拒绝原假设的最小显著水平。由于所建立的假设检验为双边检验,所以p值[18]为 (12) 在给定的显著水平α下,若p>α,则接受原假设H0,说明失效模式i、j在统计上独立;若p≤α,则拒绝原假设H0,说明失效模式i、j在统计上显著相关。 3.2 Delta方法 (13) (14) 根据式(11)即可计算出检验统计量Wij。 燃料电池发动机是燃料电池轿车的核心部件,属于复杂的机电液一体化系统,失效模式不唯一,失效模式间的相关性难以判别,导致无法准确评价其可靠性水平。 本文中对118辆集中示范运行的燃料电池轿车的可靠性试验数据进行统计分析,运用所提出的竞争失效模式统计相关性分析模型研究燃料电池发动机首次失效模式的相关性。燃料电池发动机主要存在4类典型的首次失效模式,如表1所示,各类失效模式的累积分布如图2所示。发生任意一类失效模式,燃料电池发动机则停止工作,须进行故障排查。 表1 燃料电池发动机典型失效模式 4.1 模型参数估计 针对燃料电池发动机首次故障的失效模式数据,选择对数正态分布建立竞争失效模式相关性分析可靠性模型,利用模拟退火算法对条件极大似然估计量θ=(μ,M)中的14个模型参数进行最优化求解。 4.2 相关性假设检验 表2 相关矩阵的p值 根据假设检验原则,当p>0.05时,失效模式i、j独立;当p≤0.05时,失效模式i、j相关。由表2可知,失效模式(1,4)、(2,4)和(3,4)统计上失效独立,而失效模式(1,2)、(1,3)和(2,3)统计上失效相关。从失效机理角度加以分析,“电流短路危险”产生的极间短路电流会对单电池性能产生影响,导致“单电池电压低于下限值”。由于电堆中单电池的串联结构,单电池的异常会影响整个电堆的性能和安全,所以“单电池电压低于下限值”势必会对电堆电压产生影响,导致“单电堆电压低于下限值”。然而,由于密封部件磨损或是供电接触器故障引起的“气泵故障”属于耗损失效,从功用的角度而言,对单电池及电堆的性能无直接影响,因此它们的失效模式之间不存在相关性。 (1)本文中提出了一种基于竞争风险理论的失效模式相关性统计分析模型。选择多元对数正态分布函数建立系统的潜在联合失效分布模型,对竞争失效模式的相关关系进行描述,避免了传统竞争风险模型中做独立性假设的必要。推导出在某组件失效时,系统内其它组件均正常的条件概率,建立条件极大似然函数,运用模拟退火算法对极大似然估计量中的多个模型参数进行全局最优解搜寻。 (2)在大样本情况下,根据极大似然估计量的渐近正态性,构造出服从标准正态分布的检验统计量,利用Delta方法对相关矩阵的方差进行求解,并建立相关性p值假设检验,在95%的置信水平下,通过p值来判别与量度任意两两失效模式之间的相关性。 (3)运用本文中提出的模型与方法分析了燃料电池发动机竞争失效模式之间的相关关系,这样既可以在改进设计阶段帮助开发人员改善系统的薄弱环节,更合理地确定系统可靠性指标,保证整车可靠性分配与预测的正确性;亦可以为维修人员提供更有效的维修策略,对系统进行预防性维护,避免关联故障的发生。基于上述研究,下一步将针对可维修系统建立竞争失效模式相关性分析模型。 [1]HaoP,FengQM,CoitDW.ReliabilityandMaintenanceModelingforSystemsSubjecttoMultipleDependentCompetingFailureProcesses[J].IIETransactions, 2010, 43(1): 12-22. [2] 喻天翔, 孙玉秋, 张祖明. 多模式失效的机械零件可靠度计算新理论[J]. 机械工程学报, 2003, 39(3): 134-138. [3]DavidHA,MoeschbergerML.TheTheoryofCompetingRisks[M].London:Griffin, 1978. [4]KimCM,BaiDS.AnalysesofAcceleratedLifeTestDataUnderTwoFailureModes[J].InternationalJournalofReliability,QualityandSafetyEngineering, 2002, 9(2): 111-125. [5] 谭源源, 张春华, 陈循. 竞争失效场合步进应力加速试验统计分析[J]. 航空学报, 2011, 32(3): 429-437. [6]SatowT,OsakiS.OptimalReplacementPoliciesforaTwo-unitSystemwithShockDamageInteraction[J].Computers&MathematicswithApplications, 2003, 46(7):1129-1138. [7]Elandt-JohnsonRC.ConditionalFailureTimeDistributionsUnderCompetingRiskTheorywithDependentFailureTimesandProportionalHazardRates[J].ScandinavianActuarialJournal, 1976, 1: 37-51. [8] Cornell C A. Bounds on the Reliability of Structural Systems[J]. Journal of Structural Divison, ASCE, 1967, 93(1): 171-200. [9] Ditlewsen O. Narrow Reliability Bounds for Structural Systems[J]. J. Structural Mechanics,1979,7(4): 453-472. [10] 喻天翔, 宋笔锋, 万方义, 等. 机械零件多失效模式相关可靠度算法研究[J]. 机械强度, 2006, 28(4): 508-511. [11] Kaishev V K, Dimitrova D S, Haberman S. Modelling the Joint Distribution of Competing Risks Survival Times Using Copula Functions[J]. Insurance:Mathematics and Economics, 2007, 41(3): 339-361. [12] 唐家银, 何平, 梁红琴, 等. 多故障模式高长寿命产品相关性失效的综合可靠性评估[J]. 机械工程学报, 2013, 49(12): 176-182. [13] Hechman J J, Honore B E. The Identifiability of the Competing Risks Model[J]. Biometrika, 1989, 76(2): 325-330. [14] Meeker W Q, Escobar L A. Statistical Methods for Reliability Data[M]. New York: John Wiley & Sons, 1998. [15] 王建宏. 丢失数据下的条件极大似然辨识[J]. 控制与决策, 2014, 2: 358-362. [16] Abbasi B, Eshragh Jahromi A H, Arkat J, et al. Estimating the Parameters of Weibull Distribution Using Simulated Annealing Algorithm[J]. Applied Mathematics and Computation, 2006, 183(1): 85-93. [17] Louit D M, Pascual R, Jardine A K S. A Practical Procedure for the Selection of Time-to-failure Models Based on the Assessment of Trends in Maintenance Data[J]. Reliability Engineering & System Safety, 2009, 94(10): 1618-1628. [18] 谢光军, 胡茑庆, 秦国军. 涡轮泵振动参数与统计特征量的线性相关性分析[J]. 推进技术, 2005, 26(6): 540-543. [19] Escobar L A, Meeker W Q. The Asymptotic Equivalence of the Fisher Information Matrices for Type I and Type II Censored Data from Location-scale Families[J]. Communications in Statistics-Theory and Methods 2001, 30(10): 2211-2225. [20] Nelson W B. Accelerated Testing: Statistical Models, Test Plans, and Data Analysis[M]. New York: John Wiley & Sons,2009. Statistical Correlation Analysis on the Multiple Failure Modes of a Fuel Cell Engine Based on Competing Risks Chen Tie1, Zheng Songlin1,2, Liu Xintian1& Feng Jinzhi1,2 1.CollegeofMechanicalEngineering,UniversityofShanghaiforScienceandTechnology,Shanghai200093;2.MachineryIndustryKeyLaboratoryforMechanicalStrength&ReliabilityEvaluationofAutoChassisComponents,Shanghai200093 To overcome the difficulties in discriminating and measuring the correlation between multiple failure modes of complex systems, a statistical correlation analysis model for multiple failure modes is proposed based on competing risks theory. The combined failure distribution of the system is established with multivariate lognormal distribution, and a conditional probability-based maximum likelihood function is constructed with its estimates optimized by using simulated annealing algorithm. In large sample condition, the asymptotic covariance matrix of maximum likelihood estimates is obtained by means of Fisher information matrix, and then Delta method is used to derive the variance of correlation matrix. Then, p-values hypothesis testing procedures are developed to discriminate the relationship and degree of correlation between competing failure modes. Finally an analysis on the fault data of a fuel cell engine is conducted to verify the feasibility and effectiveness of the model built. The research provides a theoretical basis for the reliability prediction and allocation of competing failure system and a technical foundation for the study on optimal maintenance strategy. fuel cell engine; competing failure modes; failure correlation; multivariate lognormal distribution; simulated annealing algorithm; hypothesis testing * 国家863计划项目(2011AA11A265和2012AA110701)、国家自然科学基金(51375313)、上海市科委基础研究重点项目(13JC1408500)和上海市研究生创新基金(JWCXSL1401 & JWCXSL1302)资助。 原稿收到日期为2014年7月18日,修改稿收到日期为2014年8月24日。3 相关性假设检验


4 模型的试验验证
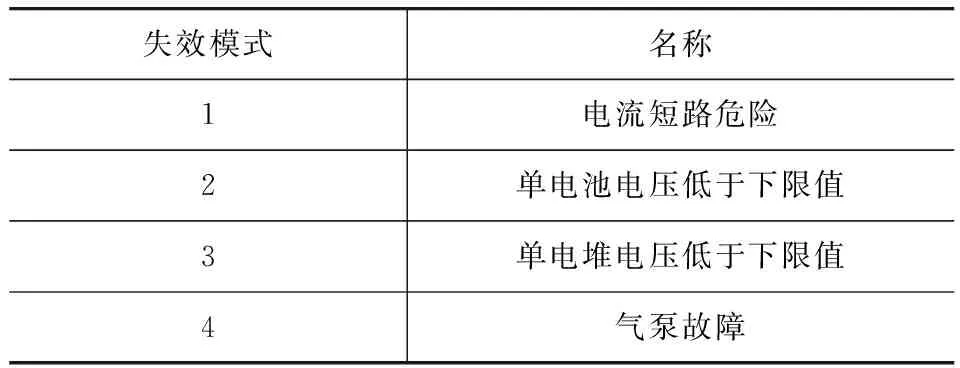

5 结论
