基于改进隐马尔科夫模型的畜禽全基因组关联分析中的多重检验方法

梅步俊　王志华

摘 要：为了改进在畜禽全基因组关联分析中，利用隐马尔可夫模型（HMM）进行多重检验时的过学习问题，提出将人工神经网络算法（ANN）作为预处理，引入畜禽全基因组关联分析中，较好地弥补了已有的多重检验方法的缺陷，提高了统计推断性能，其运算速度也显著提高。

关键词：全基因组关联分析；隐马尔科夫模型；人工神经网络；多重比较；假设检验

中图分类号 S852 文献标识码 A 文章编号 1007-7731（2015）10-22-03

Abstract：In order to improve the learning problem of hidden Markov Model（HMM）for multiple testing in whole-genome Association analysis of livestock and poultry，a algorithm of artificial neural network（ANN）as a pretreatment is proposed in multiple testing methods of genome-wide association analysis of livestock and poultry. Results showed that it just well make up for the deficiencies of multiple testing methods based on HMM，and improve the performance of statistical inference，and its speed is also improved significantly.

Key words：Genome-wide association study（GWAS）；Hidden Markov Model（HMM）；Artificial neural network（ANN）：Multiple comparisons； Hypothesis testing

全基因组关联分析（Genome-Wide Association Studies，GWAS）是基于“常见疾病，常见变异（common disease，common variant）”的假设，利用标记和突变位点在群体水平的连锁不平衡检测QTL。这种关联性的产生是由于当前群体携带有源于共同祖先的染色体片段，这些片段包含相同的QTL等位基因或单倍型。一般认为，对于复杂性状，除了受少数几个效应较大的基因控制外，还受许多微、中效基因控制。随着对基因组信息认识水平的的提高和高通量测序技术的发展，GWAS已经变成研究复杂性状遗传机理的重要手段。截至2014年7月，仅在人类上就有1 927篇GWAS文章发表，共报道13 418个SNP与各类性状有显著性相关。国内外不少研究者对畜禽的重要经济性状、遗传缺陷性疾病、复杂疾病的抗性、品种特征等性状也开展了GWAS。Zhang等[1]使用澳大利亚996头婆罗门牛和1 097头有6次产犊记录的母牛进行繁殖性状的遗传评估。Santana等[2]使用720头公瘤牛的平均日增重（ADG）和354 147SNP数据进行GWAS，采用混合模型和回归方法检测到3号染色体上的6个SNP与ADG显著相关。显著性最高的SNP（p=9.49×10-8）解释了5.62%的表型方差。

大尺度多重检验（large scale multiple test）是现代统计学的重要研究领域，广泛应用在GWAS、DNA芯片分析和脑图像分析等领域。在这些研究中，常常同时检测数以万计甚至百万假设检验。在GWAS中，常常使用Bonferroni矫正多重比较问题，但是由于连锁不平衡，SNP之间是不独立的，这与传统假设检验所有假设之间独立、所有样本来源于单一分布不同。例如，不同的基因可能在同一通路中，这些基因表现较强的相关性。畜禽群体中，由于个体之间存在亲缘关系和共同环境效应，这都会对多重检验造成显著影响。Finner和Roters[3]、Owen[4]研究表明假设检验间的相关性显著影响Ⅰ型错误率的期望和方差。Sun和Tony等[5]应用复合决策理论，由隐马尔科夫模型（HMM）研究假设检验间不独立情况下的多重检验问题，构建“局部显著性指数”（local index of significance，LIS）替代p值，改进了假设检验间不独立情况下的假发现率（false discovery rate，FDR）性能。Wei和Sun等[6]应用类似的方法发展了“汇集局部显著性指数”（pooled local index of significance，PLIS）控制FDR，该方法具有最小的假阴性率（false negative rate，FNR），比传统的基于P值的假设检验方法有更高的功效。Li和Wei等[7]利用SNP间的LD信息作为先验信息，建立加权LD图模型，应用马尔科夫随机场模型（Markov random field model，HMRF）控制GWAS中的假发现率。但基于单倍型的方法可能由于自由度太高、单倍型推断中的错误和单倍型包含SNP数的武断性而损失功效。现有基于HMM的多重检验方法存在过学习的问题，训练出的模型可能存在过拟合情况。本研究将人工神经网络算法（ANN）和HMM结合，ANN算法具有很强的抗干扰性，也不存在过学习的问题，弥补了HMM的缺陷，提高了多重检验的功效。

1 研究背景

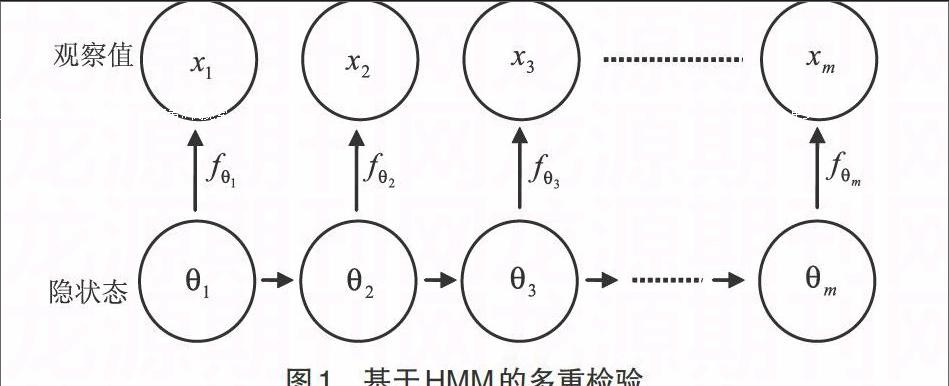
1.1 隐马尔可夫模型 设[θ=θm1=θ1，…，θm]是服从伯努利分布的随机变量，[θi=0]表明变量[i]来源于零假设，反之来源于非零假设。假设观察值[x=x1，…，xm]由以下条件概率产生：

1.3 人工神经网络算法（ANN）人工神经网络是一种应用类似于大脑神经突触联接的结构进行信息处理的数学模型。神经网络是一种运算模型，由大量的节点（或称神经元）之间相互联接构成。每个节点代表一种特定的输出函数，称为激励函数（activation function）。每2个节点间的连接都代表一个对于通过该连接信号的加权值，称之为权重，这相当于人工神经网络的记忆。网络的输出则依网络的连接方式，权重值和激励函数的不同而不同。鉴于ANN和HMM的互补性，利用ANN的长处来克服HMM的不足，将ANN作为HMM的预处理部分，利用ANN的抗干扰能力改进HMM的过学习，具有预测精度高、耗时少的特点。

2 材料与方法

2.1 第15届QTL-MAS公共数据集 该公共数据由一个远交群体构成，使用 LDSO 软件[9]模拟产生。历史群体首先模拟了1 000个世代，每个世代1 000个个体，随后模拟30个世代，每个世代150个个体。基因组共模拟了5条染色体、9 990个 SNP标记，每条染色体长度1M（Morgan），携带均匀分布的SNP标记1 998个（相邻SNP标记间距0.05cM）。最终用于基因组选择评估的数据由3 220个个体组成，其中包括20头公畜、200头母畜（每头公畜与10头母畜交配）和3 000个后裔（每头母畜生产 15 个后裔）。所有个体都模拟了9 990个SNP 标记的基因型，并且没有基因型缺失或判型错误。每头母畜的15个后裔中，有10个模拟了一个连续性状的表型值。2 000个有表型值的后裔及其它1 000个没有表型值（但有模拟的真实育种值）的后裔，分别作为参考群和验证群。

2.2 模拟数据 全基因组数据模拟需要首先定义基因组的结构。与基因组结构相关的参数包括：染色体长度（Lc）、染色体数（Nc）、总标记数（Nm）、标记位置的分布和基因数或数量性状基因座（QTL）数（NQTL）。为便于模拟，一般设定不同染色体的长度相同，为1M（Morgan），不同染色体上的标记数目一般也假设相同。

2.3 模拟研究 结合HMM和ANN，利用ANN弥补HMM的不足。HMM训练模型主要基于最大似然准则（Maximum Likelihood，简称ML）和最大共有信息准则（MaximumMutual Information，简写为MMI），采用梯度法计算，更新HMM模型中的参数。采用最小均方误差（MMSE）准则，ANN提高HMM的识别能力，保证H0，H1推断的正确性。具体步骤：建立3层ANN结构（一个输入层，一个隐含层，一个输出层）和随机初始ANN神经元链接权重，由n个输入节点和n个输出节点组成。采用类似于交叉验证策略，将模拟数据真实值作为输入，训练链接权重。将ANN算法的输出，输入到HMM模型中，采用Baum-Welch算法得出对数似然值，应用梯度下降法调整模型参数。测试的误差评价准则为平均相对误差：

3 结果与分析

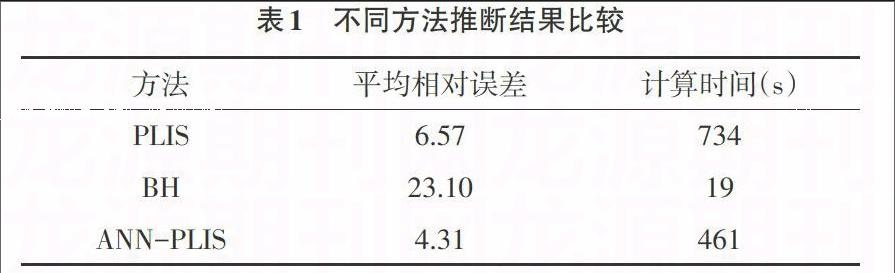
研究采用自编软件产生模拟数据，结合公共数据集，将ANN和HMM相结合，提出改进PLIS法-ANN-PLIS。通过比较PLIS、BH[11]、ANN-PLIS的预测性能，结果表明，ANN-PLIS较单纯使用HMM的PLIS运算速度很快，ANN-PLIS具有很强的鲁棒性、记忆能力、非线性映射能力以及强大的自学习能力，运算速度也大大加快，提高了多重比较过程的准确性（表1）。但是ANN也有其缺点：（1）最严重的问题是没能力来解释自己的推理过程和推理依据；（2）不能向用户提出必要的询问，而且当数据不充分的时候，神经网络就无法进行工作；（3）把一切问题的特征都变为数字，把一切推理都变为数值计算，其结果势必是丢失信息；（4）理论和学习算法还有待于进一步完善和提高。

致谢：本研究部分灵感及部分计算设备由中国农业大学动物科技学院张勤教授课题组提供。

参考文献

[1]Zhang，Y.D.，et al.. Genomic selection for female reproduction in Australian tropically adapted beef cattle[J]. Animal Production Science，2014，54（1）：16-24.

[2]Santana，M.H.，et al.，Genome-wide association study for feedlot average daily gain in Nellore cattle（Bos indicus）[J]. J Anim Breed Genet，2014，131（3）：210-216.

[3]Finner，H.，M. Roters. Multiple hypotheses testing and expected number of type I[J].Ann. Statist.，2002：220-238.

[4]Owen，A..Variance of the number of false discoveries[J].Journal of the Royal Statistical Society 2005，B（67）：411-426.

[5]Sun，W.，T. Tony Cai. Large-scale multiple testing under dependence[J]. Journal of the Royal Statistical Society：Series B（Statistical Methodology），2009，71（2）：393-424.

[6]Wei，Z.，et al..Multiple testing in genome-wide association studies via hidden Markov models[J].Bioinformatics，2009，25（21）：2802-2808.

[7]Li，H.，Z. Wei，J. Maris. A hidden Markov random field model for genome-wide association studies[J]. Biostatistics，2010，11（1）：139-150.

[8]Wenguang，S.，T.T. Cai，Large-scale multiple testing under dependence[J]. Journal of the Royal Statistical Society Series B，2009，71（2）：393-424.

[9]Ytournel，F..Linkage disequilibrium and QTL fine mapping in a selected population[J].Station de Génétique Quantitative et Appliquée，INRA，2008.

[10]Meuwissen，T.，M. Goddard.Accurate Prediction of Genetic Values for Complex Traits by Whole Genome Resequencing[J].Genetics，2010，185：623-631.

[11]Benjamini，Y.，Y. Hochberg.Controlling the False Discovery Rate：A Practical and Powerful Approach to Multiple Testing[J].Journal of the Royal Statistical Society. Series B（Methodological），1995，57（1）：289-300. （责编：张宏民）