混合动力传动系扭转振动特性分析*

张志飞，孙风建，徐中明,贺岩松，杨 益

(1.重庆大学，机械传动国家重点实验室，重庆 400030； 2.重庆大学机械工程学院，重庆 400030)



2015097

混合动力传动系扭转振动特性分析*

张志飞1,2，孙风建2，徐中明1,2,贺岩松1,2，杨 益2

(1.重庆大学，机械传动国家重点实验室，重庆 400030； 2.重庆大学机械工程学院，重庆 400030)

混合动力汽车传动系与传统汽车的传动系相比在扭转振动特性上表现出新的特点，本文中采用集中质量参数法在AMEsim中建立了转矩耦合式混合动力传动系的扭振分析模型，计算了传动系的扭振固有特性，对其主要各阶扭振模态进行了分析。基于混合动力电机控制系统引入的PI控制参数和扭振分析模型，研究了PI控制的增益参数对传动系固有特性的影响。结果表明，比例控制参数会改变系统模态阻尼比，而积分控制参数则影响传动系的刚体模态，导致低阶的扭转频率和模态振型发生改变。

混合动力传动系；扭转振动；固有特性；PI控制参数

前言

扭转振动是车辆振动的一种主要形式，是影响车辆NVH(noise, vibration & harshness)性能的一个重要因素。当传动系发生扭转共振时，会导致车辆零部件工作可靠性降低，并引起车身垂向和纵向振动，对行驶车辆的乘坐舒适性有重要的影响[1]。基于经典力学的扭转振动模型是研究传动系扭振的重要手段[2-3]，文献[4]中基于灵敏度分析提出了动力学修改的方法，用来指导动力传动系统中结构参数的修改与优化。

由于混合动力传动系与内燃机传动系在结构上的区别，针对混合动力传动系的新特点，国内外学者在原有研究的基础上进行了不同的探索。文献[5]中利用Adams软件对混合动力汽车轴系机电耦合动力学特性进行了分析，文献[6]中通过扭转减振器的刚度匹配实现了某功率分流式混合动力传动系共振转速的优化，文献[7]中采用数值模拟方法分析了功率分流式混合动力传动系的低频扭振特性。不过，直接针对混合动力传动系扭振的研究很少涉及控制参数的影响。

本文中以某款转矩耦合式混合动力传动系为研究对象，建立动力传动系扭振模型，计算并分析该传动系的固有特性和模态振型。基于传动系的扭振分析模型，针对混合动力传动系引入的电机控制参数，讨论PI控制参数对混合动力传动系固有特性的影响。

1 扭转振动固有特性计算与分析

1.1 扭振模型的建立

该混合动力电动车采用发动机后置后驱的布置形式，发动机和电机并联布置，来自发动机的动力经变速器减速增矩后通过锥齿轮与电机的动力进行转矩的耦合，再经过传动轴、差速器、半轴的传递驱动整车。图1为该混合动力传动系结构示意图。

该车采用3轴式5挡变速器，由于变速器挂不同挡位对整个传动系固有特性的影响并不明显[1],本文中以变速器挂4挡(传动比为1.54)为例对传动系进行研究。采用惯性元件和柔性单元简化系统的子单元，系统主要的惯性元件为飞轮、变速器、动力耦合齿轮、差速器输入轴、差速器齿冠、车轮和车体；柔性部件为离合器、变速器轴、传动轴、半轴和轮胎。电机传动轴和电机端的锥齿轮以转动惯量的形式附加在变速器输出轴上；轮胎与地面之间的接触采用齿轮齿条模拟，忽略轮胎的滑移效应，仅考虑轮胎的扭转刚度，采用扭转弹簧模拟其扭转特性。

在AMEsim中，惯性元件采用集中质量参数模型描述，柔性元件采用弹簧阻尼元件模拟[8]。最终建立的7自由度扭振分析模型如图2所示。模型参数主要包括转动惯量和轴系刚度，其中转动惯量参数从零件的三维模型中提取，刚度参数采用材料力学计算和有限元相结合的方法获得，模型参数汇总见表1。

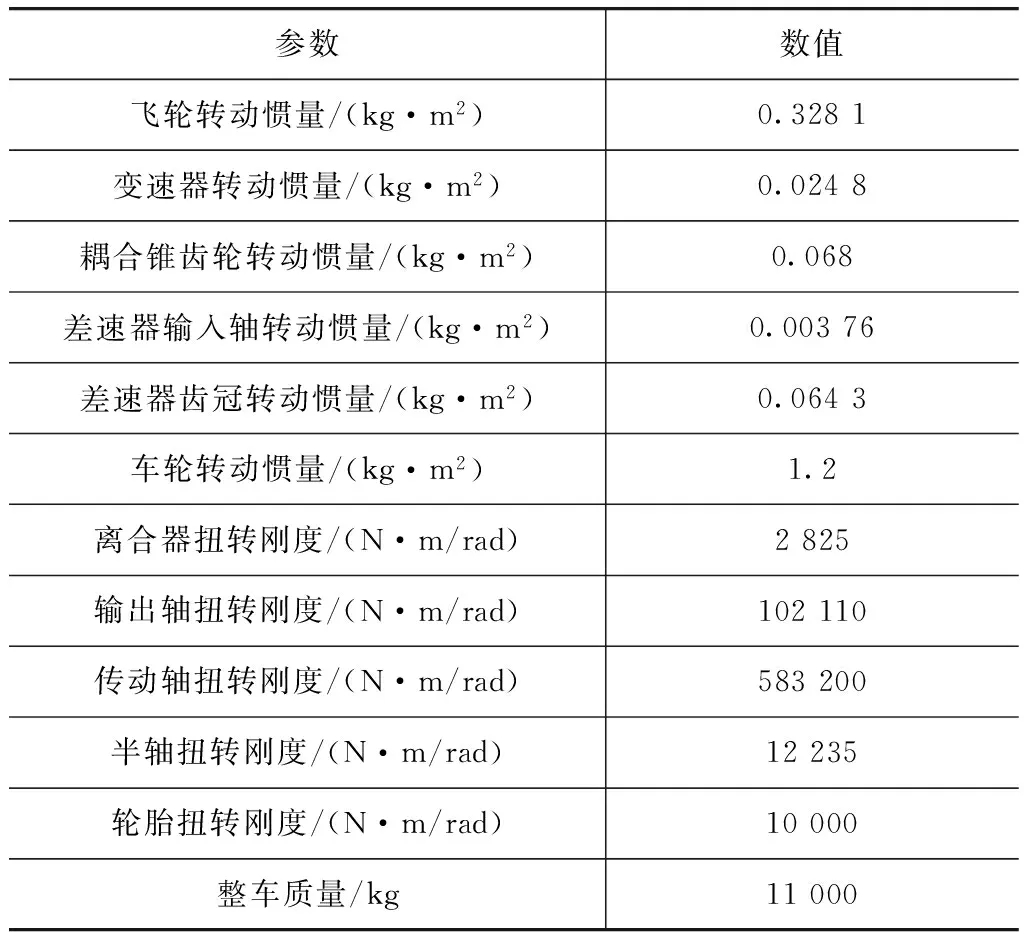
表1 传动系扭振参数

1.2 固有特性计算

传动系扭转振动的微分方程为

(1)

式中：J为系统转动惯量矩阵；C为柔性部件的阻尼矩阵；K为柔性部件的刚度矩阵；T为转矩阵；θ为振动系统的整体坐标向量。

在求解固有频率时，一般将系统设置为无阻尼的自由振动，即令阻尼矩阵C和激励转矩向量T为零，则微分方程简化为

(2)

模型前3阶固有频率为0描述了车体纵向、啮合齿轮刚体模态和耦合装置引入的刚体模态，计算得到的模型前4阶固有频率如表2所示。通过与不加装动力耦合装置的原传动系固有频率的比较可以看出，加装在变速器后端的耦合装置增加了整个传动系的转动惯量，使各阶固有频率都有不同程度的降低，而第4阶的固有频率改变最大，由429Hz变为283Hz。

表2 固有频率 Hz

图3为前4阶非零模态的振型图，横坐标的1～7分别代表飞轮、变速器、耦合锥齿轮、差速器锥齿轮、差速器齿冠、车轮和整车。

各阶模态振型的特点描述如下。

第1阶振型为传动系“颤振”，从模态振型图可以看出，传动系由飞轮至车轮的振幅逐渐减小，扭转变形的节点位于差速器和车轮之间的半轴处，半轴处的模态应变能最大，无阻尼自由振动，相位角取0°或180°，从相位上看传动系前端(飞轮-变速器-差速器)的振动与后端(车轮-车体)的振动方向相反，表现为车身沿纵向的前后振动。该振动常发生在传动系转矩突变的工况下，如踩加速踏板或松加速踏板的过程中。

第2阶振型为轮胎对称模态，车轮处的振动最大。传动系前端的振动幅度较小，此频率下的振动主要表现为左右车轮的扭转振动。由于轮胎特殊材料的摩擦特性，使其能量损耗因子较大，在车辆正常行驶时该模态对传动系扭转振动特性的影响并不大。

第3阶振型为飞轮模态，发动机端的振动与飞轮后端的振动方向相反，变速器、后桥端小幅同向扭转，节点位于飞轮与变速器之间，离合器处的应变能最大，而变速器端的振幅较大，该模态对变速器的影响较大，在发动机的谐波激励下容易引起变速器空套齿轮的“拍齿”噪声[9]。

第4阶振型为变速器扭转模态，发动机端和后桥端的振动较小，节点位于变速器轴上。由于存在齿轮间隙，该模态会被变速器啮合齿轮的啮合转矩激励，与3阶模态一样，容易引起变速器空套齿轮的“拍齿”噪声。

2 电机控制参数对传动系的影响

2.1 混合动力耦合装置分析模型

混合动力与传统内燃机车相比，采用了更为复杂的电机控制系统，根据不同的工况，通过控制电机的转速或转矩调整发动机的工作特性，使发动机工作在最佳燃油经济性工况下，从而降低燃油消耗[11]。

图4为该混合动力驱动系统的示意图，采用的是单轴式转矩合成并联混合驱动系统，这种驱动系统对电机的控制要求较低，发动机的转速一般要随行驶工况的变化而变化。

发动机转矩Te、转速ne，电机转矩Tm、转速nm与输出转矩Tout、输出转速nout满足以下关系式：

Tout=i1Te+i2Tm

(3)

(4)

式中：i1、i2分别为变速器传动比和耦合齿轮转动比。可以看出，在不同的工况下，可以采用适当的控制策略，控制电机的转矩而使发动机工作在恒定的转矩。现代混合动力汽车控制策略中，最简单有效的控制策略为PI控制。本文中以PI控制为目标控制器，分析控制参数的引入对传动系固有特性的影响，在AMEsim中建立PI控制器模型，如图5所示。

采用PI控制对电机转矩进行调节，其转矩满足：

(5)

(6)

式中：CE、KE分别为采用PI控制的电机引入的阻尼矩阵和刚度矩阵,其中，CE由控制参数KP和传动比iC决定，KE由控制参数KI和传动比iC决定；Teout为发动机和电机联合驱动引入的转矩矩阵。

由式(6)可以看出，采用PI控制对电机转矩进行控制后，动力系统中引入了额外的刚度和阻尼，由式(5)和式(6)可以看出，PI控制的比例参数(P部分)影响了系统的阻尼，而积分参数(I部分)影响了系统的刚度，根据动力学方程，扭振系统的固有频率必将发生改变，且引入转矩控制后，转矩耦合装置的一个自由度被约束，导致转矩耦合装置的刚体模态

变为非刚体模态。

为了更准确地反映控制参数的影响，须计算传动系的扭振阻尼，而对于汽车传动系而言，目前还没有一种合适的理论计算或试验方法可以比较准确地确定阻尼值，考虑到本文中只是定性地研究控制系统参数对传动系固有特性的影响，故参考其他文献[12-13]中传动系部件的阻尼值进行分析。

由于控制参数的引入，耦合装置的刚体模态变为非零扭转模态，在整个控制参数改变的过程中，该模态的频率在0.1～0.5Hz之间，对整个传动系的扭振特性不会产生影响。

2.2 控制参数KP对模态的影响

保持控制参数KI的值不变(取0.02)，使KP的值在0～20的范围变化。控制参数KP主要影响系统的阻尼特性，图6为前3阶模态的阻尼比随控制参数KP的变化关系图。由图可见：随着控制参数KP的增加，第1阶模态阻尼比逐渐增大，当KP增至8.8时，阻尼比变为1，系统1阶模态变成临界阻尼状态；第2阶模态阻尼比随KP的增加而增加，2阶模态保持为欠阻尼状态；第3阶模态阻尼比随控制参数增大而增大，当KP为13.6时，阻尼比变为1，第3阶模态变成临界阻尼状态。由此可见，第1、3阶模态的阻尼比对控制参数KP更为敏感，而第2阶模态的阻尼比受KP的影响较小。

2.3 控制参数KI对模态的影响

保持控制参数KP的值不变(取0.2)，使KI的值在0～10的范围变化，以分析控制参数KI的变化对前3阶固有频率和扭转振型的影响。

图7为前3阶频率随控制参数KI变化的曲线。由图可见：当改变KI值时传动系第1阶和第3阶固有频率变化较大，随积分常数的增大，第1阶固有频率从3.03Hz提高到5.24Hz，第3阶固有频率先从40.5Hz降至极小值39.95Hz(KI=0.5时)，再线性增高到41.48Hz；而第2阶固有频率几乎不受控制参数的影响，KI由0变到20的过程中，仅增加了0.04Hz。根据前面的分析，传动系第1阶、第3阶模态分别为“颤振模态”和“飞轮模态”，第2阶为“轮胎模态”，故采用不同的控制参数，会对传动系飞轮端和桥壳半轴处扭振频率的分布产生影响。

图8为控制参数KI分别取0、2、4、6和10时前3阶模态的振型图，因整车各阶模态的振幅为零，故横坐标未予标出。

可以看出，KI对第1阶模态振型有影响，飞轮(横坐标标号1)的幅值随KI的增加而增大，变速器和耦合锥齿轮(横坐标标号2和3)的幅值随KI的增加稍有减小，受影响的部位主要在传动系前端，节点位置并未发生改变仍位于半轴处，振型仍保持为传动系“颤振模态”。第2、3阶的振型受控制参数KI变化的影响很小，各部位的振动幅值和系统的节点位置基本不变。

3 结论

建立了某转矩耦合式混合动力传动系的扭振模型，计算并分析了其固有特性。针对混合动力电机系统的引入，分析了PI控制参数对传动系固有特性的影响，表明比例控制参数KP对模态阻尼比有较大的影响，而积分控制参数KI对模态频率有较大的影响。结果表明，混合动力传动系统中电机控制参数会影响传动系扭转振动的固有特性，合理选择电机控制参数可以调节传动系的低频扭振。

[1] Farshidianfar A, Ebrahimi M, Bartlett H. Hybrid Modeling and Simulation of the Torsional Vibration of Vehicle Driveline Systems[J]. Proc Instn Mech Engrs,2001(215):217-229.

[2] 邬惠乐,邵成,冯振东,等.解放牌CA-10型汽车动力传动系的扭振振动[J].吉林工业大学学报,1982(3):8-20.

[3] 刘辉,项昌乐,郑慕侨.车辆动力传动系通用扭振模型的研究[J].中国机械工程,2003(15):1282-1285.

[4] 刘辉,项昌乐,郑慕侨.车辆动力传动系固有特性灵敏度分析及动力学修改[J].汽车工程,2003,25(6):591-594.

[5] 岳东鹏.轻度HEV混合动力系统轴系机电耦合动力学特性研究[D].天津:天津大学,2005.

[6] 韩兵,蔡忆昔,张彤.功率分流混合动力传动系统扭转振动分析与刚度匹配[J].农业机械学报,2011,42(6):12-16.

[7] Marcus Schulz. Low Frequency Torsional Vibrations of a Power Split Hybrid Electric Vehicle Drive Train[J]. Journal of Vibration and Control,2005,11:749-780.

[8] AMESim Reference Manual[G].2008.

[9] Thomas Wellmann. Aspects of Driveline Integration for Optimized Vehicle NVH Characteristics[C]. SAE Paper 2007-01-2246.

[10] 梁锐.电动车动力传动系统扭转振动研究[D].上海:同济大学,2008.

[11] 钱立军,赵韩.混合动力汽车传动系结构分析[J].合肥工业大学学报,2003(26):1121-1126.

[12] 陈琳.混合动力轿车动力传动系冲击和振动分析研究[D].长春:吉林大学,2006.

[13] Crowther Ashley R, Zhang Nong. Development of a Clunk Simulation Model for a Rear Wheel Drive Vehicle with Automatic Transmission[C]. SAE Paper 2005-01-2992.

Analysis on Torsional Vibration Characteristics of Hybrid Powertrain

Zhang Zhifei1,2, Sun Fengjian2, Xu Zhongming1,2, He Yansong1,2& Yang Yi2

1.ChongqingUniversity,StateKeyLabofMechanicalTransmission,Chongqing400030;2.CollegeofMechanicalEngineering,ChongqingUniversity,Chongqing400030

The powertrain of hybrid electric vehicle (HEV) exhibits new features in torsional vibration characteristics, compared with that of conventional vehicles. In this paper, lumped mass parameter method is adopted to set up a torsional vibration analysis model with AMEsim for the powertrain of a torque-coupling type HEV, and the natural characteristics of powertrain torsional vibration are calculated with its modes of main orders analyzed. Based on PI control parameters introduced in motor control system of HEV and torsional vibration analysis model, the effects of gain parameters of PI control on the natural characteristics of powertrain are studied. The results show that the variation of proportional parameter may change the modal damping ratio while integral parameter may affect the rigid body modes of powertrain, leading to the changes in low-order frequencies and mode shapes of torsional vibration.

hybrid powertrain; torsional vibration; natural characteristics; PI control parameters

*重庆市科技攻关项目(CSTC2012GG-YYJS60001)资助。

原稿收到日期为2013年9月3日，修改稿收到日期为2013年12月13日。