时标上的一类二阶中立型方程正解的存在性
2015-04-11邸聪娜邵香媛王玉宽
邸聪娜,邵香媛,王玉宽
(河北科技师范学院数学与信息科技学院,河北 秦皇岛,066004)
时标上的一类二阶中立型方程正解的存在性
邸聪娜,邵香媛,王玉宽
(河北科技师范学院数学与信息科技学院,河北 秦皇岛,066004)
考虑时标上具有正负系数的二阶非线性中立型动力方程正解的存在性,首先构造适当的时标上的连续算子,再利用Banach压缩映射原理,最后得出其正解存在的充分条件。
时标;中立型;正解;非线性
关于中立型微分方程振动性的研究,在理论上和实际应用中都有着及其重要的意义[1~4]。自从Stefan Hilger提出时标理论[5],对导数和微分赋予了新的定义,很多学者便致力于时标上中立型方程振动性的研究[6~11]。文献[11]中作者考虑了
正解的存在性。笔者将其推广到非线性情况,考虑时标上具有正负系数的二阶非线性中立型动力方程
(1)
其中τ(t),γi(t),δj(t)∈Crd(T,T),τ(t),γi(t),δj(t)
为了方便,本次研究假设关于t的不等式(如未说明的)是对一切足够大的实数t成立的。并考虑如下假设:
(H1)fi(0)=0,gj(0)=0;且fi,gj均满足Lipchitz条件,即对于某区域D,存在常数Lfi(D)>0,Lgj(D)>0,使得对∀x≥0,y≥0,有|fi(x)-fi(y)|≤Lfi(D)|x-y|和|gj(x)-gj(y)|≤Lgj(D)|x-y|。
首先利用时标上的导数积分运算,链式法则,含参量积分求导,构造适当的连续算子,再利用Banach压缩映射原理,最后得出正解存在的充分条件。
1 预备知识
定义1[5]设T为时标,对t∈T,定义前跳算子σ:T→T,σ(t)=inf{s∈T:s>t},后移算子ρ;T→T,ρ(t)=sup{s∈T:s>t},而μ:T→[0,∞),μ(t)=σ(t)-t。如果σ(t)>t,则称t是右疏的;而如果ρ(t)
定义2[5]设f:T→R,如果f在T的右稠密点连续,左稠密点存在有限极限,则称f是rd连续的。把所有rd连续的函数组成的集合记成Crd=Crd(T)=Crd(T,R)。
2 定理及证明
假设supT=∞,且定义[t0.tif,+∞)={t∈T,t0≤t<+∞},给出正解的存在性定理。


(2)
(3)
(4)
(5)

易知T1是连续的。由条件(H1)和(4)式,对∀x∈Ω1及t≥t1,在此有
另一方面,由定理的条件及(2),(5)式,可得
从而a1≤T1x≤A1。因此,T1Ω1⊂Ω1。又对∀x1,x2∈Ω1, t≥t1,由条件(H1)及(2),(3)式,可得
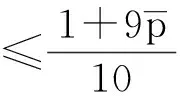






由Banach压缩映射原理知,存在x(t)∈Ω1使得T1x(t)=x(t),将T1x(t)=x(t)代入方程(1)计算得,x(t)就是方程(1)的一个最终正解。证毕。
定理2 若方程(1)满足条件(H1)和(H2),并且存在两个常数p1,p2,使得1≤p1≤P(t)≤p2<+∞,则方程(1)一定存在一个最终正解。

(6)
(7)
(8)

易知T2是连续的,由定理条件及(6)式,对∀x∈Ω2, t≥t2,有
另一方面,由定理条件及(7)式得
从而a2≤T2x≤A2,因此T2Ω2⊆Ω2。又对∀x1, x2∈Ω2, t≥t2,由条件(H1)及(8)式,可得





由Banach压缩映射原理知,存在x(t)∈Ω2使得T2x(t)=x(t),将T2x(t)=x(t)代入方程(1)计算得,x(t)就是方程(1)的一个最终正解。证毕。
注:对于-1 本次研究将文献[11]中的二阶中立型方程推广到非线性方程,利用Banach压缩映射原理,得到非线性方程非振动的充分条件,完善了时标上中立型方程的非振动性理论。 [1] L H Erbe,W K Kong,B G Zhang.Oscillatory theory for functional differential equation[M].New York:Dekker,1995. [2] ZHANG Zhen-guo,YANG Ai-jun,DI Cong-na.Existence of positive solutions of second-order nonlinear neutral differential equations with positive and negative terms[J].JOURNAL OF APPLED MATHEMATICS and COMPUTION,2007,25:245-253.[3] YU Yuan-hong,WANG Hong-zhou.Non-oscillatory solutions of second-order non-linear neutral delay equations[J].J Math Anal App1,2005,311:445-456. [4] LI W.Positive solutions of second-order nonlinear differential equations[J].J Math Anal App1,1998,211:326-337. [5] Bohner M,Peterson A.Dynamic Equations on Time Scales:An Introduction with Applications[M].Boston:Birkhäuser,2001. [6] 陈大学,刘洁纯.具有分布时滞的二阶非线性中立型时标动力方程的振动定理[J].系统科学与数学,2010,30(9):1 191-1 205. [7] 杨军,陈雁东,张忠军,等.时标上具有正负系数的中立型时滞动力方程的稳定性[J].黑龙江大学自然科学学报,2012,29(2):160-164,168. [8] 杨红玉,葛琦,余秀萍,等.二阶时标非线性中立型动力学方程的振动性[J].数学的实践与认识,2008,38(18):253-256. [9] Liuailian,Wuhongwu,Zhsiming.Oscillation nonautonomous neutral dynamic delay equations on time scales[J].Acta Mathematica Scientia,2006,26B(1):99-106. [10] Ravi P Agarwal,Donal O’Regan,S H Saker.Oscillation Criteria for Second-Order Non-linear Neutral Delay Dynamic Equations[J].Mathematical Analysis and Applications,2004(300):203-217. [11] 邸聪娜,李民良,郭雅彩,等.时标上具有振动系数的中立型动力方程非振动解的存在性[J].河北科技师范学院学报,2010,24(1):50-53. (责任编辑:朱宝昌) The Existence of Positive Solution for Second-order Neutral Dynamic Equations on Times Scales DI Cong-na,SHAO xiang-yuan,WANG Yu-kuan (School of Mathematics and Information Science & Technology,Hebei Normal University of Science & Technology,Qinghuangdao Hebei,066004,China) This paper studied the existence of non-oscillatory solutions for the second-order nonlinear dynamic equations with the positive and negative coefficients. By defining continuous operators and using Banach fixed theorem on the time scales, the sufficient condition of the existence of positive oscillatory solutions for the above equations is obtained. time scales;neutral term;positive solution;non-linear 10.3969/J.ISSN.1672-7983.2015.02.007 秦皇岛市科学技术局秦皇岛市软科学研究计划项目(项目编号:201302A250)。 2015-04-12; 修改稿收到日期: 2015-05-26 O175.13 A 1672-7983(2015)02-0031-05 邸聪娜(1983-),女,讲师,硕士。主要研究方向:微分方程的稳定性与振动性。3 结 论
