一类周期函数在Hölder空间中的插值逼近

何尚琴，刘继发，赵会娟

(河北科技师范学院数学与信息科技学院,河北 秦皇岛,066004)



一类周期函数在Hölder空间中的插值逼近

何尚琴，刘继发，赵会娟

(河北科技师范学院数学与信息科技学院,河北 秦皇岛,066004)

利用一类插值算子，研究了在Hölder空间中以2π为周期的反周期函数的三角插值的逼近和饱和问题，并讨论了其在该空间中的饱和及充要条件。

Hölder空间；反周期三角插值算子；饱和阶

插值是很多研究问题讨论的对象，插值所面临的第一个问题是根据插值问题的需要来选择插值函数类或插值函数空间。如果选择的函数类为三角多项式，就称为三角插值问题[1]。由于广泛的理论和实践的需要，三角多项式插值的研究在近些年来发展很快，人们在推导周期函数的数值积分、积分方程和奇异积分方程等数值解的公式时，三角插值成为必不可少的工具。

关于2π周期函数的三角插值问题已有很深入的研究及推广，Sharma A和Varma A K[2]研究了2π周期函数的(0,m)三角插值。反周期函数的三角插值问题，自Delvos F J，Knoche[3]的研究之后，反周期函数的插值问题受到广泛关注[4,5]。

Hölder空间是一类十分有用的函数空间，研究此空间的性质具有重要的意义，在此空间中定义的范数同样具有优越的性质。蒋艳杰[6]研究了在Hölder度量下，一类三角插值多项式的逼近和饱和问题，确定了饱和类和饱和阶。随后侯象乾[7]又研究了在Hölder空间下，双周期(0,m)三角插值多项式(m为偶数)的逼近与饱和，确定了饱和阶与饱和类。笔者研究在Hölder度量下，以2π为周期的反周期函数的三角插值算子及其在Hölder空间中的逼近问题。

记AC={f|f∈C2π,f绝对连续}，Hα={f|f∈C2π,f∈Lipα},

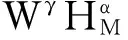
1 主要结论

定理 设f(x)∈Wm-1Hα,即f(x)是Hölder空间中以2π为周期的反周期函数，当m为奇数时，有

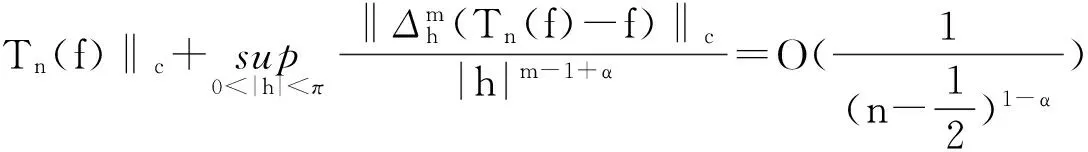
2 相关引理

易知插值算子J2n-1(x)在所取结点处满足插值条件：

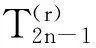
3 定理证明

充分性的证明。

应用m-1次拉格朗日中值定理，

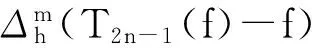
日本作为一个四面环海的岛国，本土资源贫乏，贸易立国是其国家战略，故日本经济的海外依存度极高，进口资源的稳定供应和贸易通道的畅通，直接关系着日本经济的兴衰。据统计,日本石油进口的80%以上和国际贸易的70%都是经由南海航线，[19]日本经济很容易因周边海域与海上航道爆发危机或遭遇封锁而陷入瘫痪状态，为此，日本基于“保卫周边海域和确保海洋运输安全对日本国家安全至关重要”这一考虑，而将南海纳入其需要关注的周边海域和海上交通线，并且从经济、政治、外交和军事等方面多管齐下，以增强自身对南海地区的地缘政治影响力。

f(m-1)(x+θ(m-1)h)]/hα‖c

必要性的证明：

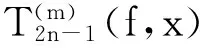
由T2n-1(T2n-1(f))=T2n-1(f)得

综上，笔者利用插值算子

[1] 谢庭藩,周颂平.实函数逼近论[M].杭州:杭州大学出版社,1998.

[2] Sharma A,Varma A K.Trigonometric interpolation[J].Duke Math J,1965,32:341-357.

[3] Delvos F J，Knoche L．Lacunary interpolation by antiperiodic trigonometric polynomials[J].BIT,1999,39:430-450.

[4] 何尚琴,侯象乾.反周期函数(0,m)三角插值的收敛性[J].宁夏大学学报：自然科学版,2006,27(3):218-220,224.

[5] 何尚琴,李艳坡.反周期函数的缺项2-周期三角插值[J].河北师范大学学报：自然科学版,2013,37(6):541-548.

[6] 蒋艳杰.在度量下一类三角插值多项式的逼近[J].北京师范大学学报：自然科学版,1993,29(1):50-54.

[7] 侯象乾.一类三角插值多项式在度量下的逼近[J].宁夏大学学报：自然科学版,2001,22(3):282-283.

[8] Butzer P L,Nessel R J.Fourier analysis and approximation volume 1[M].New Yourk:Birkhauser Basel and Academic Press,1971.

(责任编辑：朱宝昌)

Approximation of Certain Trigonometric Interpolation in the Hölder Metric

HE Shang-qin，LIU Ji-fa，ZHAO Hui-juan

(School of Mathematics and information Science & Techonology,Hebei Normal University of Science & Technology, Qinhuangdao Hebei,066004,China)

By using a class of interpolation operator, the 2π trigonometric approximation and saturation of antiperiodic function were studied on the Hölder Metric, the necessary and sufficient condition were discussed.

Hölder space；antiperiodic trigonometric interpolation operator;the saturation order

10.3969/J.ISSN.1672-7983.2015.02.006

2015-04-15; 修改稿收到日期: 2015-05-26

O174.41

A

1672-7983(2015)02-0027-04

何尚琴(1977-)，女，讲师，硕士。主要方向：函数逼近论。