时标上二阶动力方程m点边值问题的正解
2015-04-11武利猛申玉发郑国萍杨晓静
武利猛,张 娟,申玉发,郑国萍,杨晓静
(1 河北科技师范学院数学与信息科技学院,河北 秦皇岛,066004;2 河北科技师范学院科研处)
时标上二阶动力方程m点边值问题的正解
武利猛,张 娟,申玉发,郑国萍,杨晓静
(1 河北科技师范学院数学与信息科技学院,河北 秦皇岛,066004;2 河北科技师范学院科研处)

时标;边值问题;正解
近年来,时标作为数学的一个新研究分支已引起了许多学者的广泛关注。一方面,它统一和推广了现有的微分方程和差分方程的理论;另一方面,时标上动力方程的研究对于刻画真实现象和过程的数学模型有着重要应用。例如:时标上的种群动力学、流行病模型、金融消费过程的数学模型等。 越来越多的学者对在时标上利用不动点定理解决动力方程的边值问题产生了很大兴趣[1~7]。目前,关于时标上二阶混合导数动力方程m点边值问题正解存在性的文章并不多见[8,9]。笔者借助于Guo-Krasnosel'skii不动点定理和Leggett-Williams不动点定理得到了至少存在2个正解和3个正解的判别条件,其中本次研究所讨论的边值问题在方程类型上有别于文献[8,9],所得结果推广了文献[3]的研究结果。
本次将研究时标T上具有混合导数的动力方程m点边值问题
(1)
(2)

假设下列条件成立
(H1) q(t)∈Cld([t1,t2],[0,∞)),且存在t0∈[t1,t2],使得q(t0)>0。
(H2) f:[t1,t2]×[0,∞)→[0,∞)连续,且在T的任意一个包含t0的子集上f(t,·)>0。
在给出主要结果之前,先介绍一些基本定义和引理。
定义1 令Banach空间E=Cld[t1,t2]且范数‖u‖=supt∈[t1,t2]|u(t)|,定义锥P⊂E,且P={u∈E|u在[t1,t2]中是凹的,非增且非负}。
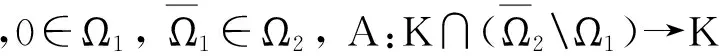
(A1) ‖Au‖≤‖u‖,∀u∈K∩∂Ω1,且‖Au‖≥‖u‖,∀u∈K∩∂Ω2
或者
(A2) ‖Au‖≥‖u‖,∀u∈K∩∂Ω1,且‖Au‖≤‖u‖,∀u∈K∩∂Ω2
引理2[3](Leggett-Williams不动点定理) 令P是实Banach空间E中的锥。定义
Pr={u∈P:‖u‖ (B1) {u∈P(ψ,q,l);ψ(u)>q}≠φ,且对于u∈P(ψ,q,l), ψ(Au)>q。 (B2) ‖Au‖ (B3) ψ(Au)>q,对于u∈P(ψ,q,r)且‖Au‖>l。 为了研究边值问题(1),(2),首先研究如下形式的线性m点边值问题 (3) (4) 引理3 如果h(t)∈Cld(T,R),那么边值问题(3),(4)有唯一解 (5) 证明 对式(3)从t1到t进行积分,得到 (6) 再对式(6)从t1到t进行积分,得到 (7) 令t=ξi,t2分别代入式(6),有 (8) (9) (10) 令t=ξi,t2分别代入式(7),可得 (11) (12) (13) 将式(10),(13)代入式(7),可以在[t1, t2]得到式(5)。 证明 由uΔ(t)=h(t)≤0, 得到u(t)在[t1, t2]是凹的,那么uΔ(t)是递减的。uΔ(ξi)≤uΔ(t1), i=1,2,…m-2, 由式(3) 知 引理5 如果u∈P,则 (14) 易知边值问题(1),(2)有解, u=u(t)当且仅当u是算子方程的不动点。 则边值问题(1),(2)至少有2个正解u1(t)和u2(t),使得0≤‖u1(t)‖≤p1≤‖u2(t)‖。 证明 由条件(H1),(H2),引理4和引理5可知AP⊂P。容易验证A:P→P是全连续映射。设Ω1={u∈E:‖u‖ 则由(i)可知 从而可知‖Au‖≥‖u‖, u∈P∩∂Ω1。 首先,工具便利引发民意浪潮。新媒体平台上“人人都是发言人”,对政策的态度和情绪能够随时随地“漂入”政治流中,而数据库的存在进一步使得这些民意在短期内不会“漂出”,决策者需要时可以进行批量采集和提取,为政策变迁提供民意依据和参考。因此,新媒体工具大大增强了公众参与政策讨论的效能感,网络民意不断涌现。在本研究采集的500条微博文本中,有43条微博反映了普通公民的政策意向,占“政策观点”类样本总量的37.5%,远远高于传统媒体中民意表达的数量占比。 设Ω2={u∈E:‖u‖ 令Ω3={u∈E:‖u‖<λR},选取u∈P且‖u‖=λR,有 综上讨论可知边值问题(1),(2)至少有2个正解u1(t)和u2(t),使得0≤‖u1(t)‖≤p1≤‖u2(t)‖。 证毕。 推论1 假设下列条件成立: (C1) f0=f∞=∞; 则边值问题(1),(2)至少有2个正解u1(t)和u2(t),使得0≤‖u1(t)‖≤p1≤‖u2(t)‖。 定理2 假设条件(H1),(H2)成立, 0 则边值问题(1),(2)至少有3个正解u1(t), u2(t), u3(t)使得‖u1‖ 由bλ∈P(ψ,b,bλ)且ψ(bλ)=bλ>b,{u∈P(ψ,b,bλ):ψ(u)>b}≠φ,选取u∈P(ψ,b,bλ),则b≤u(ξm-2)≤u(t)≤‖u(t)‖≤bλ, t∈[t1, ξm-2]。 由条件(ii),当t∈[t1, ξm-2]得 由条件(iii)可知,当‖u‖≤a得 从而可知引理2中的条件(B2)成立。 例1 令T=[0,1]∪[2,3]考虑边值问题 (15) (16) (17) (18) [1] Bohner M,Peterson A.Dynamic Equations on Time Scales:an Introduction with Applications[M].Boston:Birkhäuser,2001.[2] Bohner M,Peterson A.Advances in Dynamic Equations on Time Scales[M].Boston:Birkhäuser,2003. [3] Ismail Y.Existence of positive solutions for nonlinear three-point problems on time scales[J].Journal of Computational and Applied Mathematics,2007,206(2):888-897. [4] Han W,Liu M X.Existence and uniqueness of a nontrivial solution for a class of third-order nonlinearp-Laplacianm-point eigenvalue problems on time scales[J].Nonlinear Analysis,2009,70(5):1 877-1 889. [5] Sun H R,Li W T.Multiple positive solutions forp-Laplacianm-point boundary value problems on time scales[J].Applied Mathematics and Computation,2006,182(1):478-491. [6] Sun J P.Twin positive solutions of nonlinear first-order boundary value problems on time scales[J].Nonlinear Analysis,2008,68(6):1 754-1 758. [7] Song C X,Weng P X.Multiple positive solutions forp-Laplacian functional dynamic equations on time scales[J].Nonlinear Analysis,2008,68(2):208-215. [8] Liang S H,Zhang J H,Wang Z Y.The existence of three positive solutions ofm-point boundary value problems for some dynamic equations on time scales[J].Mathematical and Computer Modelling,2009,49:1 386-1 393. [9] Liu J,Sun H R.Multiple Positive Solutions form-Point Boundary Value Problem on Time Scales[DB/OL].(2010-08-10)[2015-06-30].http://www.boundaryvalueproblems.com/content/2011/1/591219. (责任编辑:朱宝昌) Positive Solutions tom-point Boundary Value Problems for Second Order Dynamic Equations on Time Scales WU Li-meng1, ZHANG Juan2, SHEN Yu-fa1, ZHENG Guo-ping1,YANG Xiao-jing1 (1 School of Mathematics and Information Technology, Hebei Normal University of Science & Technology, Qinhuangdao Hebei, 066004;2 Office of Science and research, Hebei Normal University of Science & Technology; China) time scales; boundary value problem; positive solutions 10.3969/J.ISSN.1672-7983.2015.02.005 国家自然科学基金项目(项目编号:11171113,11401385);河北省自然科学基金项目(项目编号:A2015407063);秦皇岛市科学技术研究与发展计划项目(项目编号:201401A038);河北科技师范学院博士基金资助项目(项目编号:2013YB008)。 2015-05-18; 修改稿收到日期: 2015-06-24 O A 1672-7983(2015)02-0020-07 武利猛(1983-),男,博士,讲师。主要研究方向:微分方程理论。
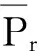



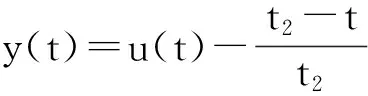
2 主要结果









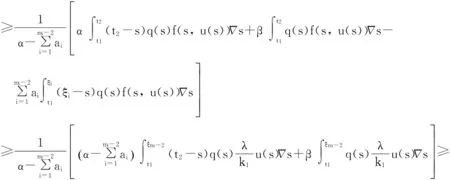

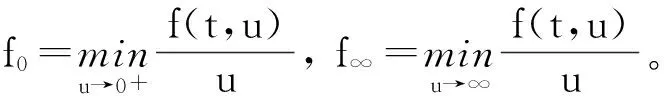

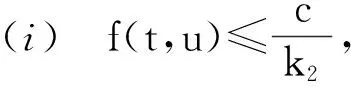

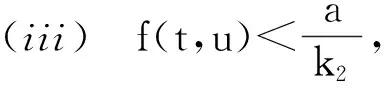

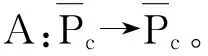



3 应用举例




