基于自适应抗差最小二乘的线路正序参数在线辨识方法

薛安成 张兆阳 毕天姝

基于自适应抗差最小二乘的线路正序参数在线辨识方法

薛安成 张兆阳 毕天姝

（华北电力大学新能源电力系统国家重点实验室 北京 102206）

针对在线PMU（Phasor Measurement Unit）数据会存在随机量测噪声甚至不良数据的实际情况，本文提出了一种输电线路正序参数的自适应抗差最小二乘在线辨识方法。文中基于线路双端多时刻断面的 PMU电气量建立了线路正序参数的最小二乘辨识模型；在简要介绍抗差最小二乘原理的基础上，为充分利用量测信息，采用IGG（Institute of Geodesy & Geophysics, Chinese Academy of Sciences）权函数（方案 I）实现“三段”法抗差参数辨识；并利用中位数原理在线估计方程残差序列的期望和方差，实现自适应地调整权函数的抗差阈值。该方法无需事先确定量测设备的量测误差，具有很好的抗差能力及结果可信度，同时也消除了参数迭代对初值的敏感性。基于PSCAD仿真和PMU实测数据的算例表明，该方法十分有效，更适合于在线参数辨识。

输电线路 正序参数 参数辨识 自适应抗差最小二乘 PMU数据

1 引言

输电线路参数是电力系统分析、运行及控制的基础，其工频参数主要有正序参数、零序参数等；线路参数的准确性会影响到电力系统如潮流计算、状态估计、网损分析、无功优化和保护整定等各种应用分析及辅助决策功能的可信度。

目前，电力部门所使用的线路工频参数大部分已采用实测参数值，但部分线路仍旧采用理论值。理论参数采用数值计算简化得出，忽略了各种因素的影响[1]；实测参数是在特定条件下通过离线停电试验[2-4]或在线带电试验[5-6]并附加额外试验设备获取的。实际上，线路参数在地理环境、运行工况及导线老化等随机因素影响下会发生缓慢变化。因此，上述途径获取的参数均会与实际值存在或多或少的差异。

另一方面，目前国内电网已大量安装了相量测量单元PMU，基本建成了基于PMU的广域测量系统WAMS。PMU具有时间同步准确度高及测量准确度高的优点[7]，为利用电网同步数据在线实时辨识电网参数提供了新的途径，引起了学者们的广泛研究。同时，鉴于 PMU提供的多为电网三相基本对称的相量，因此，利用 PMU数据进行线路正序参数在线辨识，成为目前关注的研究方向之一。

目前，利用 PMU数据的线路正序参数辨识主要分为两种：一种是结合WAMS量测和已有的SCADA量测，基于状态估计实现对线路参数的辨识[8-10]；另一种是在 PMU配置完善的情况下，利用单一设备的 PMU量测实现对单一设备参数的独立解耦辨识及在线实时辨识。显然，完全利用PMU数据辨识参数，可避免传统方法的不足，能获得准确度更高的参数[11-20]。

在完全利用PMU数据辨识线路正序参数方面，文献[15-16]基于支路两端单时刻的电压、电流PMU量测建立了参数直接求解的等式方程，并对多时间断面下近似服从正态分布的辨识结果样本采用均值估计来实现支路参数估计；文献[17-18]为保证均值估计的稳定性，采用一种方差系数判据来确定合适的样本数，具有一定的抗差能力；文献[19]提出了一种窗口滑动总体最小二乘法的参数辨识方法，该方法具有较好的抗噪声能力，但只考虑了较小的量测噪声，未考虑实测数据的量测噪声可能较大甚至有不良数据的实际情况。为此，文献[20]基于将量测分为保权区和淘汰区的“两段”抗差法，提出了具有较强抗差能力的抗差递推最小二乘方法，能够抵御不良数据对估计值的影响。

相较于只将量测数据分为正常量测（保权区）和有害量测（淘汰区）的“两段”抗差措施，更有效的措施是将正常量测细分为有效量测和可利用量测，对可利用量测降权处理[21]，这在一定程度上可以抑制较大量测噪声对辨识的影响。

另一方面，降权区和淘汰区的划分依赖于量测设备的量测误差。然而，量测设备在系统不同状况下，如不同的线路工况，其量测误差是有差异的，很难准确确定量测设备的量测误差。因此，基于人为设定的固定量测误差划分降权区和淘汰区，不能适应在线参数辨识的要求。

有鉴于此，本文提出了一种基于自适应抗差最小二乘的线路正序参数在线辨识方法，采用 IGG权函数（方案 I）实现“三段”抗差辨识，并利用对方程残差序列的期望和方差的有效估计，实现对权函数的抗差阈值的自适应调整，提高了方法的适应能力。该方法在较大量测噪声甚至不良数据存在的情况下，能获得更加准确且可信的辨识结果。

2 线路正序参数辨识的数学模型

输电线路的等值模型根据其长度可分为集中参数的精确等值模型和基于均匀传输线方程的分布参数等值模型，两种模型均可用∏型等值电路来表示，如图1所示。在此，本文只研究输电线路的集中参数等值模型的正序等值参数。

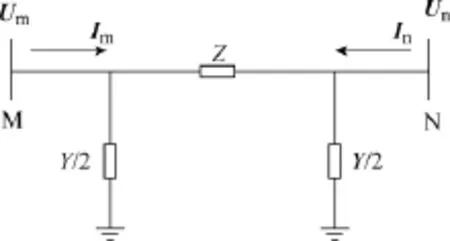
图1 线路∏型等值模型Fig.1 ∏-type equivalent circuit of transmission line

对于双端均装设PMU的线路，PMU能量测到线路两端的电压及电流矢量、有功及无功功率；根据 PMU的这些量测量，可建立线路的线性数学模型为

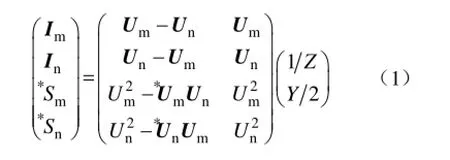
将式（1）按实部和虚部展开，并写成矩阵形式，同时考虑PMU随机量测噪声，则为

由于PMU能在较短时间内获得多组采样数据，故可利用多时间断面下的 PMU数据提高方程的冗余度，减小随机量测噪声的影响。

3 自适应抗差最小二乘ARLS(Adaptive Robust Least Squares)

3.1 抗差最小二乘的基本原理

对于参数辨识问题（见式（2）），其传统最小二乘的目标函数和相应辨识结果为

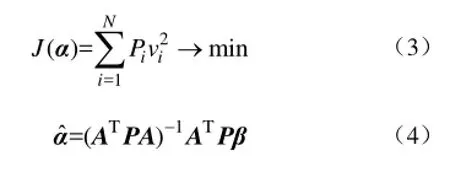
式中，N为采样时刻数，Pi为第i个量测的权重，P是对角元素为 Pi的权矩阵。

对于抗差最小二乘，其目标函数为方程残差的函数，定义为

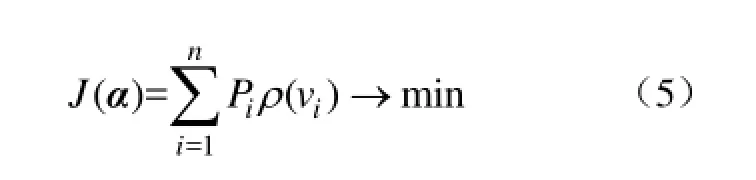
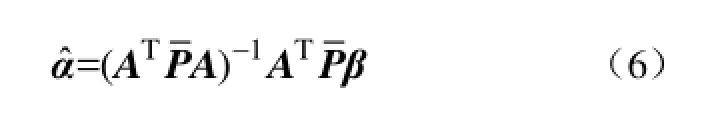
上式表明，抗差最小二乘保留了最小二乘的优点，并通过选择权函数，赋予传统最小二乘抗差能力。然而，抗差最小二乘的权是方程残差的非线性函数，需迭代求解，存在迭代收敛问题。

3.2 IGG抗差法

IGG（Institute of Geodesy & Geophysics, Chinese Academy of Sciences）抗差法（方案 I）[21]的思想是充分考虑量测数据的实际情况，对不同的量测数据采用不同的权函数及抗差准则。IGG法将量测数据分为三类，即正常量测、可利用量测及有害量测。对应地，将权分为保权区、降权区及淘汰区；相比只将量测数据分为正常量测及有害量测（或者可利用量测）的“两段”抗差法，“三段”抗差法能更充分有效地利用量测信息。

IGG抗差法的权函数为

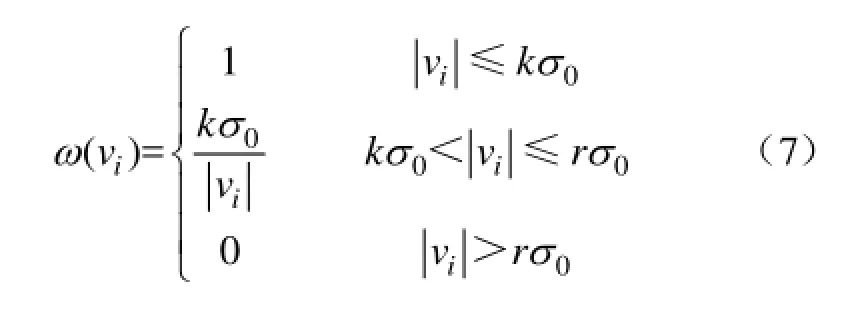
式中，vi为第 i个量测的残差；k、r为抗差阈值的调制系数，σ0为量测误差标准差。系数k可取1.0～1.5，r可取 2.5～3.0，本文取k =1.5，r=3.0。

按等价权的定义，由式（7）可推出 IGG权函数对应的极值函数为

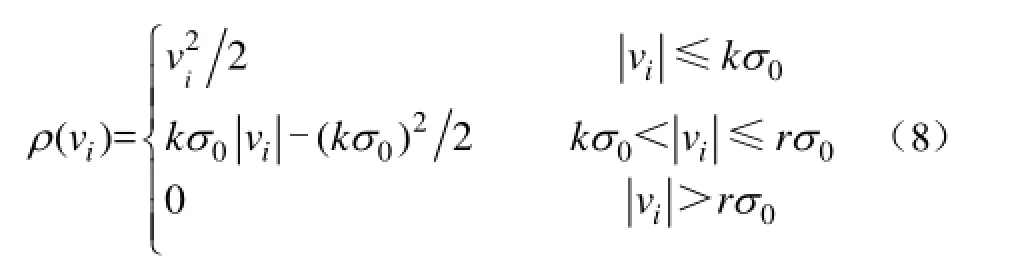
式（7）及式（8）表明，IGG抗差法将量测分为三部分，采用不同的抗差准则：①量测残差不大于kσ0时，采用最小二乘法，其权值不变为 1；②量测残差介于 kσ0和 rσ0之间时，则采用绝对值和极小法，其权值小于 1，降权处理，消弱残差较大的量测对参数辨识的影响；③量测残差大于 rσ0时，拒绝此量测，使其权值为 0，体现出抗差能力。

3.3 残差分布的自适应估计

为保证抗差最小二乘的抗差能力及辨识结果的可信度，IGG权函数需要合理地划分降权区和淘汰区，即选择合理的抗差阈值。若抗差阈值选择过大，则不能有效地抑制可利用量测甚至不能有效排除全部不良量测，从而降低算法的抗差能力；但若抗差阈值选择过小，则会排除大部分可利用量测，从而会降低辨识结果的可信度。因此，合理地选取抗差阈值，才能保证算法的有效性，并提高其适应能力。

权函数的抗差阈值取决于量测误差的标准差，但实际上，量测设备的量测误差不是一成不变的，在线路不同工况下也不完全相同。根据量测设备的固定量测误差的标准差确定抗差阈值不能满足在线参数辨识的要求。需要根据实际量测中残差序列的具体分布情况，开发辨识算法以在线自适应地估计量测残差的标准差，提高算法的适应能力。

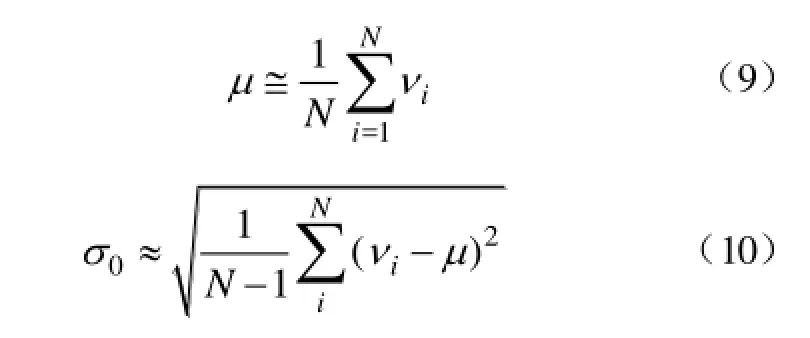
然而，对于在线实测数据，不良量测的存在会使残差序列里混杂有部分粗差；此时只是残差序列的主体部分近似服从正态分布，用式（9）、式（10）估计的μ和σ0会受到粗差的干扰而严重偏离真值。因此，需要在排除粗差的前提下，才能有效估计残差序列的分布。

为防止粗差对估计的干扰，本文基于中位数原理近似有效地估计残差序列的数学期望μ和标准差σ0，其相应的估计为[21]

在有效估计残差序列分布的基础上，可将IGG抗差法的权函数改为

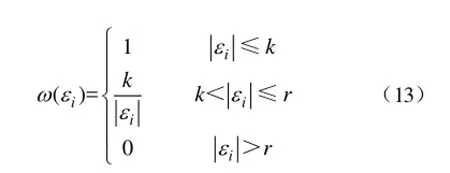
其中，εi为残差vi的正则化残差，

基于中位数原理对残差序列分布参数的有效估计，可自适应地调整权函数的抗差阈值，保证算法的抗差能力和辨识结果的可信度，提高算法对不同量测误差的自适应能力。

此外，对抗差阈值的自适应调整，消除了抗差最小二乘对参数迭代初值的敏度问题，不需要再采取其他措施选取合适的参数初值，使算法具有很强的鲁棒性。由于权函数是残差的函数，需要迭代求解，若用固定的抗差阈值在迭代初值不合理时算法有可能迭代不收敛；通过对残差序列的自适应估计及抗差阈值的自适应调整，已不存在上述初值问题。

4 在线辨识流程

根据本文建立的基于多时间断面下 PMU量测的线路参数最小二乘辨识模型，基于WAMS平台，可实现线路参数在线自适应抗差最小二乘辨识。在线参数辨识流程如图2所示。

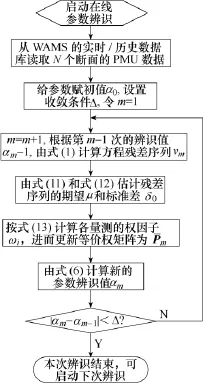
图2 在线参数辨识流程图Fig.2 The flow chart of online parameter identification

5 算例验证及分析

为表明本文所提方法的优点，以下算例中将本文ARLS方法与传统最小二乘法LS、文献[20]提出的固定抗差阈值且只具有保权区和淘汰区的“两段”抗差最小二乘法RLS进行对比。

5.1 仿真数据测试

利用PSCAD搭建单机无穷大系统。其中500kV输电线路为单回，长度为110km，正序参数设计值为电阻R=2.582Ω、电抗X=41.715Ω、全部对地电容C= 2.253μF。以线路两端稳态的正序电压、电流矢量、有功和无功作为 PMU量测量，采样频率为 100Hz，采样6s共600组的数据来辨识线路正序参数。

需要说明的是，在以下各种测试中，通过在仿真数据里叠加高斯噪声来模拟真实的实测数据；并且为避免随机的高斯噪声造成辨识结果的随机性，本文设置每一标准差的噪声分布样本数为100，取100次样本下的辨识结果的均值作为最终的参数辨识结果。

5.1.1 有效性测试

在仿真数据中叠加高斯噪声来模拟实测 PMU数据，电压电流幅值的量测误差标准差为0.2%，相角为 0.1°，功率为 0.5%[7]（以此标准差确定 RLS的抗差阈值）。在无噪声及含有高斯噪声下三种方法的参数辨识结果如表1所示。

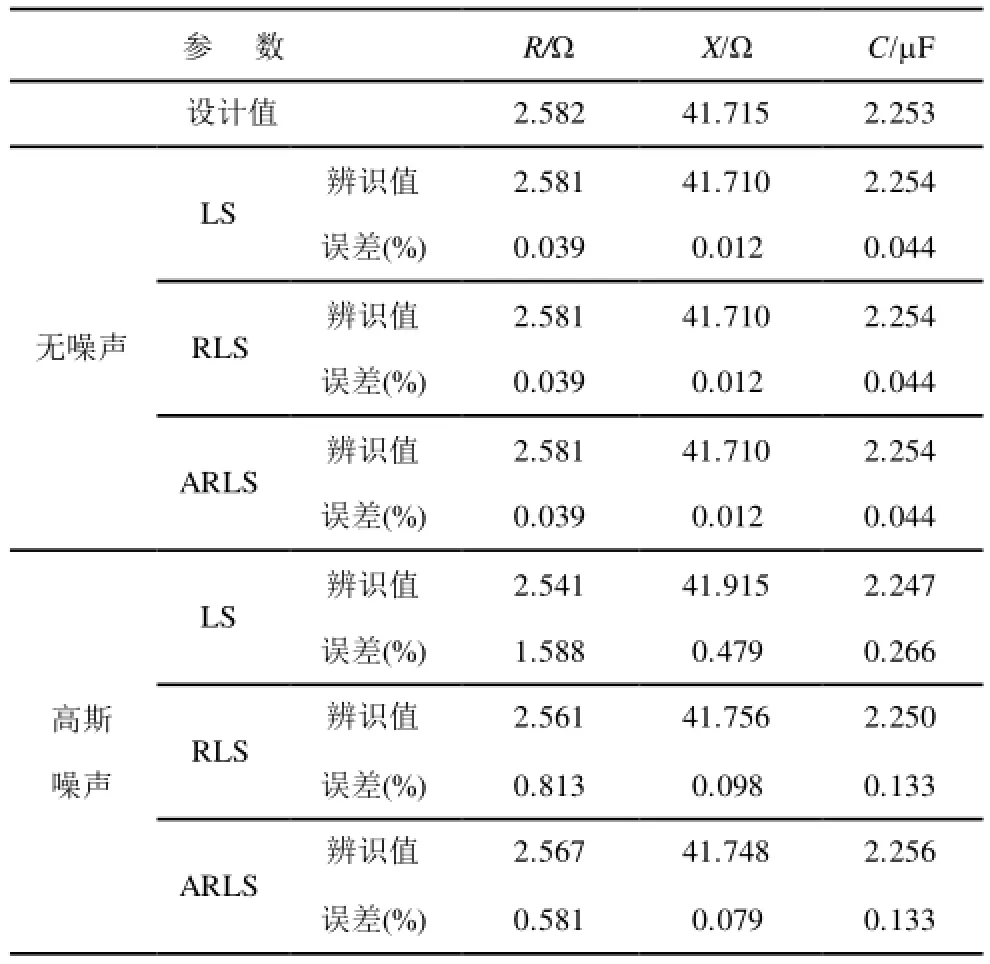
表1 有无高斯噪声下的参数辨识结果Tab.1 Identification results under the presence of Gaussian noise

表1说明三种方法在无噪声时是等价的；但量测数据含有高斯噪声时，由于ARLS采用了具有降权区的IGG权函数，能压缩残差相对较大的量测噪声，提高了辨识准确度。同时，也说明ARLS对残差序列分布的自适应估计是有效的；相对 RLS方法，该方法无需事先确定实测数据的噪声分布，适合处理没有先验知识的在线实测数据。

进一步地，在此噪声水平下，当初值偏离真值±90%时ARLS的参数迭代过程如图3所示，而初值偏离真值±50%时，RLS方法迭代已不再收敛。

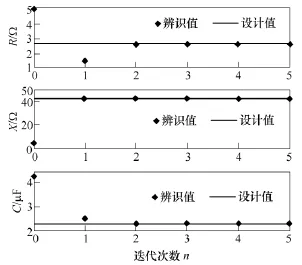
图3 初值偏离真值较大情况下的参数迭代过程Fig.3 The iterative process under the initial values deviating from the real values severely

结果表明，ARLS方法在参数迭代初值偏离真值很大时依然能快速收敛且辨识准确度很高，消除了算法对参数迭代初值的敏感性，具有较强的鲁棒性。

5.1.2 噪声抑制能力测试

在 5.1.1节叠加的噪声水平的基础上，通过不断加大电压幅值量测的噪声水平，分析ARLS的噪声抑制能力，相应的参数辨识误差如表 2所示。

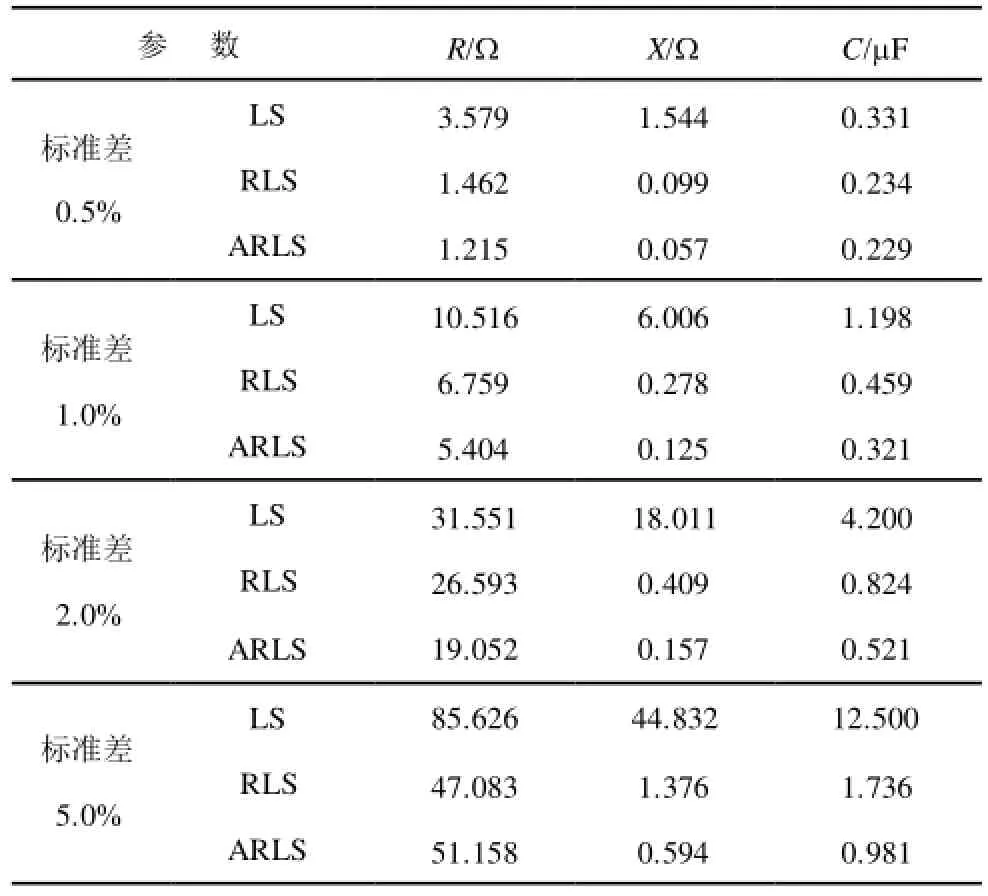
表2 不同高斯噪声水平下的辨识误差Tab.2 Identification errors under different Gaussian noises

表2表明，随着电压幅值噪声水平的提高，LS的辨识效果在恶化，而ARLS和RLS的电阻辨识效果也在恶化，但电抗和电容的辨识准确度却依然很好，并且ARLS的辨识效果要优于RLS。特别地，电阻的辨识效果不如电抗、电容好的原因，是由于电阻对电压幅值的量测噪声比较敏感[20]。测试结果再次表明，在同等噪声水平下，ARLS相较于 RLS和LS具有更强的抑制噪声能力，即ARLS通过自适应地估计残差序列的分布，进而调整具有降权区的IGG权函数的抗差阈值，提高了辨识结果的可信度。

5.1.3 抗差能力测试

在上述叠加的噪声水平的基础上，设计以下两种不良数据的情形来测试ARLS的抗差能力：①某时刻一端电压幅值量测出现20%的偏差；②某时刻一端电压幅值量测为 0。两种不良数据情形下三种方法的辨识结果如表3所示。

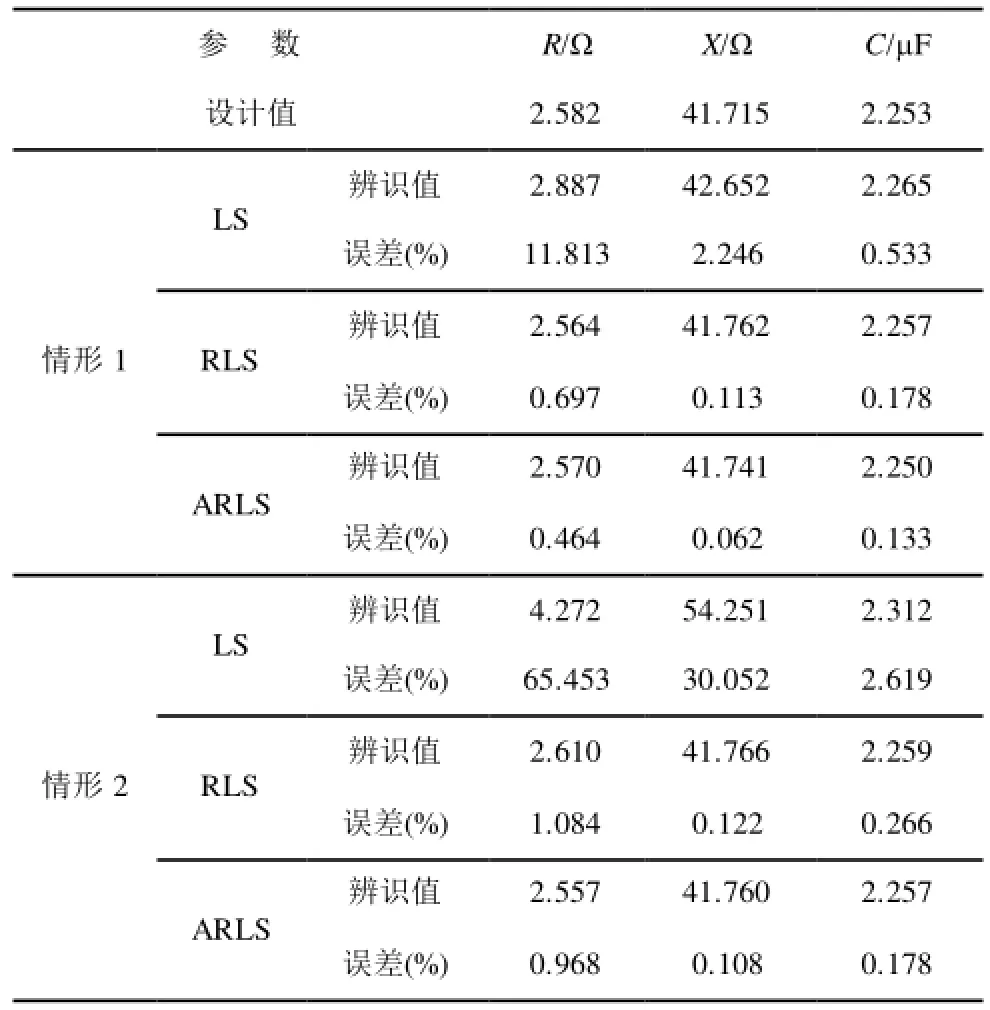
表3 不良数据情形下的辨识结果Tab.3 Identification results under different bad data

结果表明，ARLS和RLS对明显的不良数据都具有很强的抗差能力，但 LS却不具有任何抗差能力，某时刻PMU数据存在不良数据，都会使LS的辨识结果不可信。可知，相对于LS和RLS，ARLS更适合处理在线数据，更具有工程实用价值。

5.2 实测PMU数据测试

利用某电网 500kV输电线路的双端正序稳态PMU电气量来辨识线路的正序参数。此线路长115.8km，导线型号为 LGJ-4×400，无架空地线；PMU子站上传至 WAMS主站的数据间隔周期为10ms；现有1个时段共12s的数据，PMU的量测误差较小，但一端的正序电压相角在9～10s时刻出现了较大的跳变，如图4所示。

将 PMU数据均分为两段，分别以参数理论值和离线实测值作为ARLS和RLS的迭代初值的参数辨识结果如表 4、表5所示。

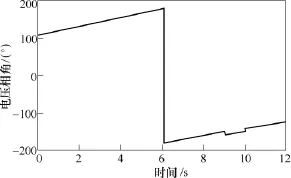
图4 正序电压相角曲线Fig.4 The phase angle curve of the positive-sequence voltage

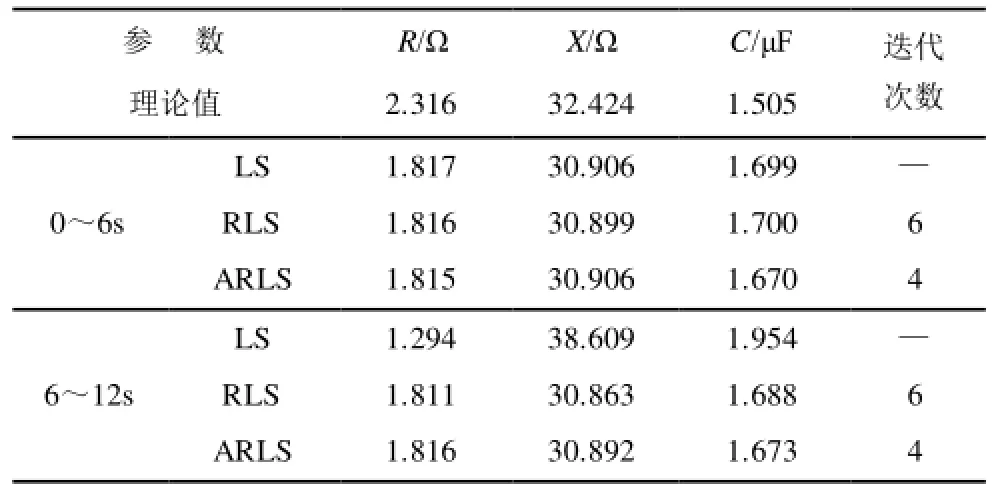
表4 以理论值为初值的参数辨识结果Tab.4 Identification results with the theoretical values for the initial values

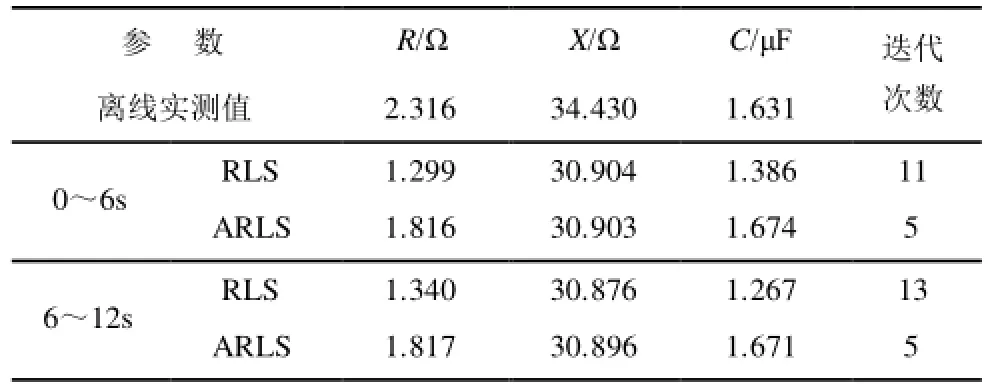
表5 以离线实测值为初值的参数辨识结果Tab.5 Identification results with the offline test values for the initial values

表4表明，在实测数据很好的情况下，三种方法的辨识效果基本相同；但实测数据存在不良数据时，LS的辨识结果已不可信，而ARLS和 RLS基本不受不良数据的影响，但ARLS方法要好于RLS，辨识结果的可信度更高些。表5和表4的对比表明，ARLS方法不受迭代初值的约束，而RLS方法在初值不合理时，参数值较小的电阻、电容的辨识结果已不可信，且迭代次数较多。因此，ARLS方法更适合用于基于实测数据的在线参数辨识。

进一步地，为表明ARLS的辨识结果有效，利用不同的参数值和线路一端的电气量去推算另一端的电气量，可获得另一端电压幅值及两端电压相角差推测值和实测值的比较，前 6s数据的拟合效果如图5所示。

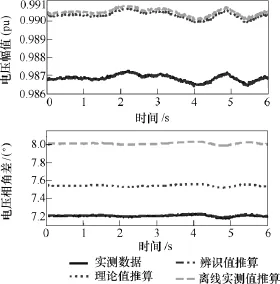
图5 电压幅值和相角差的拟合图Fig.5 The fitting figures of the voltage amplitude and phase angle difference

图5 表明用参数辨识值的拟合效果最好，而用离线实测值及理论值的拟合效果很不理想，这说明基于 PMU数据及 ARLS方法的辨识结果是十分有效的，由于其充分考虑了线路的空间布局、地理环境、运行工况及量测误差等各种因素的影响，参数辨识值更加准确可信。

6 结论

本文为利用线路双端多时间断面的 PMU数据实现线路模型正序参数的在线辨识提出了一种自适应抗差最小二乘方法。相比已有的辨识方法，该方法具有以下特点：

（1）采用IGG权函数实现“三段”法抗差辨识，能充分利用量测信息，可以很好地抑制较大量测噪声及抵御不良数据对参数辨识的不利影响。

（2）根据中位数原理在线估计残差序列的期望和方差，自适应地调整权函数的抗差阈值；不需要事先确定量测设备的量测误差，能够适应量测设备在不同运行时间及线路轻重潮流下的量测误差不同的实际情况，不仅保证了算法具有较强的抗差能力，也保证了辨识结果的可信度；同时，还消除了算法对参数迭代初值的敏感性，具有较强的鲁棒性。

基于PSCAD仿真和PMU实测数据的辨识效果表明该方法是十分有效的，也可应用到电网其他设备参数的在线辨识，具有较好的工程应用前景。

[1] 吴命利, 范瑜. 圆导线内阻抗的数值计算[J]. 电工技术学报, 2004, 19(3): 52-58.

Wu Mingli, Fan Yu. Numerical calculations of internal impedance of cylindrical conductors[J]. Transactions of China Electrotechnical Society, 2004, 19(3): 52-58.

[2] 邓春, 袁亦超, 王征, 等. 长距离输电线路工频参数测量中的数据处理[J]. 华北电力技术, 2004(2): 48-50.

Deng Chun, Yuan Yichao, Wang Zheng, et al. Data treating in measuring power frequency parameters at long distance transmission line[J]. North China Electric Power, 2004(2): 48-50.

[3] 刘遵义, 卢明, 吕中宾, 等. 特高压交流输电线路工频参数测量技术及应用[J]. 电网技术, 2009, 33(10): 59-64.

Liu Zunyi, Lu Ming, Lu Zhongbin, et al. Power frequency parameter measurement technology for UHV transmission lines and its application[J]. Power System Technology, 2009, 33(10): 59-64.

[4] 李炜, 汤吉鸿, 胡志坚, 等. 利用电压及电流双端测量信息的高压输电线路正序参数测量方法及应用[J]. 电网技术, 2011, 35(4): 103-107.

Li Wei, Tang Jihong, Hu Zhijian, et al. An approach to measure positive-sequence parameters of HV transmission line by using two-terminal measured voltage and current data and its application[J]. Power System Technology, 2011, 35(4): 103-107.

[5] 胡志坚, 刘美观, 张承学, 等. 互感线路参数带电测量研究与实现[J]. 电力系统自动化, 1999, 23(24): 32-35.

Hu Zhijian, Liu Meiguan, Zhang Chengxue, et al. Principles and realization of live line measurement to parameters of transmission lines with mutual inductance [J]. Automation of Electric Power System, 1999, 23(24): 32-35.

[6] 胡志坚, 陈允平, 徐玮. 基于微分方程的互感线路参数带电测量研究与实现[J]. 中国电机工程学报, 2005, 25(2): 28-33.

Hu Zhijian, Chen Yunping, Xu Wei. Principles and realization of live line measurement of parameters of transmission lines with mutual inductance based on differential equations[J]. Proceedings of the CSEE, 2005, 25(2): 28-33.

[7] 国家电力调度通信中心. 电力系统实时动态监测系统技术规范: 试行[EB/OL][S]. 2010.

[8] 陈晓刚, 易永辉, 等. 基于 WAMS/SCADA混合量测的电网参数辨识与估计[J]. 电力系统自动化,2008, 32(5): 1-5.

Chen Xiaogang, Yi Yonghui, et al. Network parameter identification and estimation based on hybrid measurement of WAMS/SCADA[J]. Automation of Electric Power System, 2008, 32(5): 1-5.

[9] 李钦, 项凤雏, 卢建刚, 等. 基于 SCADA及 PMU多时段量测信息的独立线路参数估计方法[J]. 电网技术, 2011, 35(2): 105-109.

Li Qin, Xiang Fengchu, Lu Jiangang, et al. An approach to estimate parameters of single transmission line based on multi-interval information measured by SCADA and phasor measurement units[J]. Power System Technology, 2011, 35(2): 105-109.

[10] 柴京慧, 李书敏, 何桦, 等. 基于PMU及多时间断面的输电网参数估计[J]. 电力系统自动化, 2009, 33(11): 49-52.

Chai Jinghui, Li Shumin, He Hua, et al. Parameter estimation based on PMU and multi-cases of SCADA for electricity transmission network[J]. Automation of Electric Power System, 2009, 33(11): 49-52.

[11] 牛胜锁, 梁志瑞, 张建华, 等. 基于多时段同步测量信息的T接线路参数在线测量[J]. 电工技术学报, 2012, 27(5): 238-244.

Niu Shengsuo, Liang Zhirui, Zhang Jianhua, et al. Online measurement of T-connection transmission line parameters based on multi-interval synchronized measurement information[J]. Transactions of China Electrotechnical Society, 2012, 27(5): 238-244.

[12] Robert E Wilson, Gary A, et al. Calculation of transmission line parameters from synchronized measurements[J]. Electric Machines and Power Systems, 1999, 27(12): 1269-1278.

[13] Shi D, Tylavsky D J, et al. Identification of short transmission-line parameters from synchrophasor measurements[C]. IEEE 40th North American Power Symposium, 2008: 1-8.

[14] 安艳秋, 高厚磊. 基于同步相量测量的线路参数在线计算[J]. 电力自动化设备, 2002, 22(9): 21-23.

An Yanqiu, Gao Houlei. On-line calculation of transmission line parameters using synchronized phasor measurement[J]. Electric Power Automation Equipment, 2002, 22(9): 21-23.

[15] 王茂海, 鲍捷, 等. 基于PMU实测数据的输电线路参数在线估计方法[J]. 电力系统自动化, 2010, 34(1): 25-27.

Wang Maohai, Bao Jie, et al. Online estimation of transmission line parameters based on PMU measurements[J]. Automation of Electric Power System, 2010, 34(1): 25-27.

[16] 王茂海, 齐霞, 牛四清, 等. 基于相量测量单元实测数据的变压器参数在线估计方法[J]. 电力系统自动化, 2011, 35(13): 61-65.

Wang Maohai, Qi Xia, Niu Siqing, et al. Online estimation of transformer parameters based on PMU measurements[J]. Automation of Electric Power System, 2011, 35(13): 61-65.

[17] 陈俊, 颜伟, 卢建刚, 等. 考虑多时段量测随机误差的变压器参数抗差估计方法[J]. 电力系统自动化, 2011, 35(2): 28-33.

Chen Jun, Yan Wei, Lu Jiangang, et al. A robust transformer parameter estimation method considering multi-period measurement random errors[J]. Automation of Electric Power System, 2011, 35(2): 28-33.

[18] 颜伟, 赵雪骞, 吕志盛, 等. 基于等式方程直接求解的支路参数抗差估计方法[J]. 电网技术, 2012, 36(6): 127-132.

Yan Wei, Zhao Xueqian, Lü Zhisheng, et al. A method to estimate branch parameters based on direct solution of equations[J]. Power System Technology, 2012, 36(6): 127-132.

[19] 毕天姝, 丁蓝, 张道农. 基于窗口滑动总体最小二乘法的输电线路参数辨识[J]. 电力科学与技术学报, 2011, 26(2): 10-15.

Bi Tianshu, Ding Lan, Zhang Daonong. Transmission line parameters identification based on moving-window TLS[J]. Journal of Electric Power Science and Technology, 2011, 26(2): 10-15.

[20] 丁蓝. 基于 PMU 的输电线路参数辨识与戴维南等值研究[D]. 北京: 华北电力大学, 2011.

[21] 周江文. 抗差最小二乘法[M]. 武汉: 华中理工大学出版社, 1997.

Online Identification of Transmission Line Positive-Sequence Parameters Based on Adaptive Robust Least Squares

Xue Ancheng Zhang Zhaoyang Bi Tianshu

（State Key Laboratory of Alternate Electrical Power System with Renewable Energy Source North China Electric Power University Beijing 102206 China）

Aiming at the actual situation that there often exist random measurement noises even bad data in online PMU(phasor measurement unit) data, a method of adaptive robust least squares is proposed for online identification of transmission line positive-sequence parameters. Firstly, the least-squares identification model of transmission line parameters is presented based on the multiperiod PMU data of both ends. And then, after the brief introduction of robust least squares, to fully use measurement information, the IGG (Institute of Geodesy & Geophysics, Chinese Academy of Sciences) weight function (scheme I) is adopted to realize “three segments” robust identification. Finally, the expectation and variance of the equation residual sequence are online estimated effectively by using the median principle to adjust the robustness threshold of IGG adaptively. The proposed method does not need to determine the measurement error of measurement equipment, and has strong robustness ability and high reliability of identification results, and also eliminates the problem that the method is sensitive to the parameter iterative initial values. The examples based on PSCAD simulation data and PMU data show that the proposed method is very effective, and is more suitable for online parameter identification.

Transmission line, positive-sequence parameters, parameter identification, adaptive robust least squares, PMU data

TM744

薛安成 男，1979年生，副教授，主要研究方向为PMU应用等。张兆阳 男，1988年生，硕士研究生，主要研究方向为线路参数辨识。

973计划（2012CB21S206），国家自然科学基金（51190103，51222703）和中央高校基本科研业务费专项资金（12MS30）资助项目。

2013-04-12 改稿日期 2013-05-26