计及撬棒保护影响的双馈风力发电机组故障电流特性研究

孔祥平 张 哲 尹项根 王 菲 隆 茂

计及撬棒保护影响的双馈风力发电机组故障电流特性研究

孔祥平 张 哲 尹项根 王 菲 隆 茂

（华中科技大学强电磁工程与新技术国家重点实验室 武汉 430074）

为了研究对称及不对称电网故障情况下双馈风力发电机组的故障电流特性，建立了两相静止坐标系下双馈风力发电机组的动态模型。对近区严重故障且撬棒保护动作情况下双馈风力发电机组的定子绕组磁链动态过程进行了研究，提出了一种兼顾精确性和简易性的定子绕组磁链简化计算模型。以此为基础，对对称故障和不对称故障情况下双馈风力发电机组的故障电流特性进行了分析，得到了其解析表达式，建立了故障电流的等效计算模型。数字仿真结果表明，理论分析结果在故障发生后的前2个工频周期内具有很高的精确度，可以满足继电保护原理研究和整定计算的应用要求。

双馈风力发电机组 撬棒保护 定子绕组磁链 故障电流特性 等效计算模型

1 引言

近年来，作为最具商业化应用前景的一种可再生能源发电技术，风力发电技术在全球范围内得到了大力发展。变速恒频双馈风力发电机组（Doubly-Fed Induction Generator，DFIG）以能量转换效率高，原动机承受的机械应力小，易于实现有功、无功功率解耦控制，具有良好的调节性能及运行稳定[1-4]等优势，在风电场中得到了广泛的应用。

然而，随着风电并网容量的不断增加，风电机组给电网安全稳定运行带来的风险日渐凸显，国内外已发生了多起风电机组大规模脱网的严重事故[5]。为了保证电网和风电机组的运行安全，一方面，各国电力公司及电网运营商纷纷提出了新的风电机组的并网规范[6-7]，要求风电机组具备故障穿越能力；另一方面，需要构建适应于风电机组接入的电网继电保护系统。故障穿越运行过程中 DFIG的运行特性将对电网的故障特征造成很大的影响，从而给继电保护的研究带来了新的问题和挑战[8]。

在电网故障情况下，电网电压骤降可能引起转子回路的过电压和过电流，从而引起励磁变流器、定、转子绕组和母线电容的损坏。为了提高DFIG故障穿越运行能力，保证故障穿越运行期间 DFIG的运行安全，一种常用的办法是安装撬棒（crowbar）保护[9-10]。当电网发生故障导致转子电流过大或直流电容电压过高时，撬棒保护断开转子侧变流器与转子绕组的连接，并通过撬棒电阻将转子绕组短路，为转子侧的浪涌电流提供一条通路。撬棒保护动作导致 DFIG失去励磁，进而从发电机运行状态转变为电动机运行状态。同时，撬棒电阻的引入导致定、转子绕组之间的耦合显著增强，使得 DFIG的运行特性不同于传统同步发电机或异步电动机。因此，有必要针对撬棒保护动作情况下 DFIG的故障特性进行研究。

迄今为止，国内外学者针对三相短路情况下DFIG 的故障电流特性开展了大量的研究[11-16]。但已有的研究成果大都处于定性分析阶段，或建立在与传统同步发电机、异步电动机故障电流特性简单类比的基础上，缺乏对撬棒保护动作后 DFIG固有特征的把握和分析。此外，目前鲜有文献探讨不对称故障情况下 DFIG故障特性。实际上，不对称短路发生的概率要远高于对称短路，开展不对称短路情况下 DFIG馈出的短路电流特性的研究是全面分析 DFIG在不同短路情况下的故障特性的重要组成部分，对适应于 DFIG大规模接入的电网保护系统的构建有重要意义。

DFIG馈出的故障电流由定子绕组电流和网侧变流器（Grid Side Converter，GSC）的交流侧电流两部分组成。鉴于 GSC容量较小，其交流侧电流对DFIG馈出的故障电流影响不大，本文主要研究DFIG的定子绕组电流特性。为了分析对称和不对称故障情况下 DFIG的故障电流特性，本文结合其结构和运行特点，建立了两相静止坐标系下 DFIG的电磁暂态方程。以此为基础，对撬棒保护动作情况下 DFIG定子绕组磁链特性进行了分析，并建立了其简化计算模型。然后，研究了对称故障和不对称故障情况下 DFIG定子绕组的故障电流特性，得到了定子绕组故障电流的解析表达式，建立了其等效计算模型。最后，数字仿真结果验证了理论分析的正确性。

2 两相静止坐标下DFIG动态模型

DFIG电磁暂态特性方程的建立，是进行短路电流分析计算的基础。定转子均采用电动机惯例时，一般化的DFIG的电压、磁链方程分别为

式中，Us、Ur、Is、Ir、Ψs和Ψr分别为定、转子电压、电流和磁链矩阵。

由于定、转子绕组间的互感矩阵是定、转子绕组轴线间夹角的周期性函数，因此三相坐标系下DFIG的电磁暂态方程是一组变系数的微分方程，不利于求解。为了简化分析，需要对 DFIG的电磁暂态方程进行坐标变换。现有文献大都采用dq坐标变换分析 DFIG的短路电流特性，即将定、转子参数全部变换到以同步速旋转的坐标系中。然而，在电网不对称故障情况下，采用dq坐标变换时需建立正、反转同步坐标系[17]，并需提取电压、电流等电气量的正、负序分量，增加了 DFIG短路电流特性分析的复杂性。由于 DFIG转子方面的结构和电气参数均对称，在分析其定子方面的对称或不对称运行问题时，将定、转子参数变换到相对定子静止的坐标系是有利的。

在两相静止αβ坐标系下，DFIG电压、磁链方程为

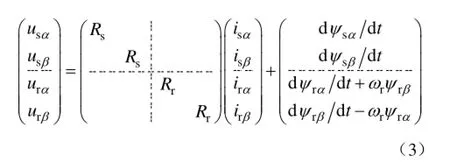
从而可以得到以定、转子绕组磁链为状态变量的状态方程为

其中

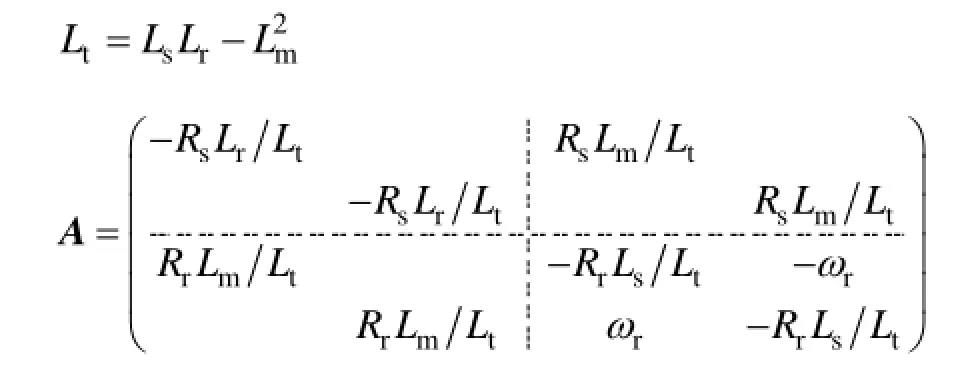
系统矩阵A的特征值决定了定、转子绕组磁链故障暂态分量的衰减时间常数和振荡频率，同时，也决定了定、转子绕组电流故障暂态分量的衰减时间常数和振荡频率。

3 近区严重故障情况下DFIG定子绕组磁链特性及简化计算模型

3.1 定子磁链特性分析

由此得到矩阵A的特征值为

式中，τAs为定子绕组磁链故障暂态分量的衰减时间常数；τAr为转子绕组磁链故障暂态分量的衰减时间常数；ωAr为转子绕组磁链故障暂态分量的振荡角频率。在这种情况下，定、转子绕组磁链可以通过两个独立的二阶系统求得。

在近区严重故障情况下，为了保证 DFIG的运行安全，撬棒保护将会动作，在断开转子侧变流器的同时通过撬棒电阻将转子绕组短路。此时转子绕组等效电阻为

式中，Rc为撬棒电阻。

在这种情况下，定、转子绕组磁链之间耦合显著增强，不能再忽略不计。因此，直接忽略定、转子绕组电阻的影响[11]或者与异步电动机的短路电流进行类比[12-13]以分析对称故障时 DFIG的短路电流将会出现较大的误差。

将式（7）中的 Rr用替换后可以得到撬棒保护动作后的新的系统矩阵Ac，将其特征值记为

针对一台 1.5MW 的 DFIG（具体参数见附录A），表1给出了不同撬棒电阻对矩阵Ac的特征值的影响。

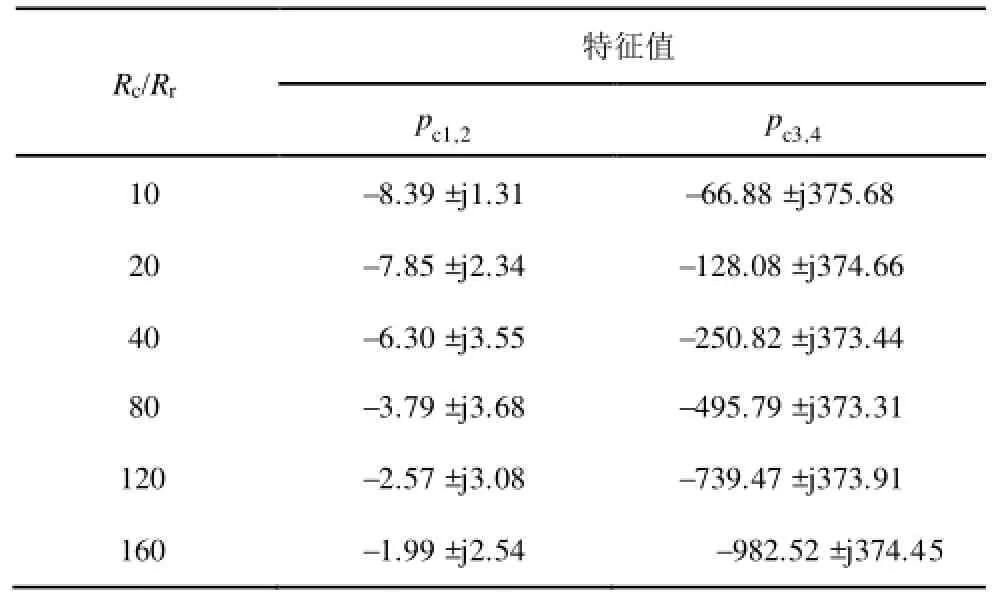
表1 撬棒电阻与系统矩阵Ac特征值的对应关系Tab.1 The eigenvalues of the system matrix

从表1可以看出，撬棒电阻对系统矩阵的特征值的实、虚部均有影响，但是撬棒电阻对故障分量的振荡频率的影响相对较小。其中，ωAcs的最大值为 3.68rad/s，ωAcr的最小值为 373.31rad/s。因此，可以近似认为

即可以近似认为定、转子绕组电流故障暂态分量中仅含有直流分量和转速频率电流分量。

随着所串入撬棒电阻的增大，τAcs逐渐减小，τAcr逐渐增大。这说明随着撬棒电阻的增大，直流分量的衰减越来越慢，而转速频率电流分量的衰减则越来越快。同时，转速频率电流分量的衰减速度远快于直流分量。

由于矩阵 Ac的特征值随着撬棒电阻的变化而变化，且定、转子磁链之间的耦合不能忽略，这导致撬棒保护动作情况下的定子绕组磁链暂态特性分析极其复杂。因此，有必要建立定子绕组磁链的简化计算模型。

3.2 定子绕组磁链简化计算模型

为了对各类故障（包括对称故障和不对故障）情况下的定子绕组磁链进行分析，假设电网发生故障时DFIG定子绕组电压为

在式（12）中，对三相电压的幅值和相位均未作特殊要求。因此，式（12）是一个通用的电压公式，适合于各类故障情况。

对式（12）进行坐标变换，得到两相静止αβ坐标系下的定子绕组电压为

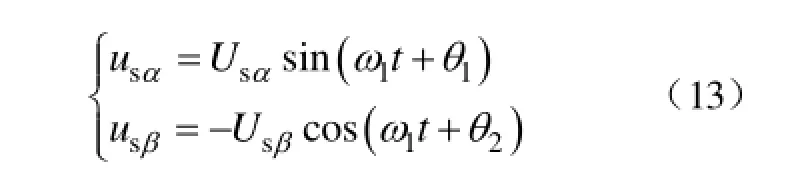
在近区严重故障情况下，虽然撬棒保护动作导致转子绕组等效电阻增大，但定子绕组电阻仍较小，可以忽略不计。将式（13）代入式（3）中的前两式，解得不计衰减时定子绕组磁链的表达式为

实际上，定子绕组电阻的实际存在使得定子绕组磁链的直流分量总是衰减的。计及衰减特性时的定子绕组磁链表达式可写为

对于衰减时间常数，文献[11-13]取为定子绕组等效时间常数，即认为。但是，如上所述，撬棒保护动作之后，导致定子绕组磁链暂态特性极其复杂。因此，上述简化处理方法会带来较大的误差。图1给出了电压对称跌落情况下根据上述简化处理得到的定子绕组磁链波形和仿真波形的对比。

图1 一般简化情况下定子绕组磁链Fig.1 The stator winding flux for conventional simplification

从图1的对比中可以看出，将式（15）中的衰减常数取为定子绕组等效时间常数将对定子绕组磁链的计算带来较大的误差，是不合理的。

为兼顾精确性和简便性，本文采用τAcs作为定子绕组磁链的衰减时间常数。图2给出了这种简化处理情况下定子绕组磁链理论波形和仿真波形的对比。

从图2的对比中可以看出，由于定、转子绕组磁链之间耦合的影响，定子绕组磁链的衰减特性非常复杂，并不能简单地用式（15）的形式表达。但是，将定子绕组磁链的衰减时间常数取为τAcs在前 4个工频周期内具有较高的精确度。这说明在前 4个工频周期内，采用τAcs作为定子绕组磁链的衰减时间常数是合理的。这对于近区严重故障情况下，短路电流最大值的计算和快速保护动作行为的分析具有重要意义。

图2 定子绕组磁链Fig.2 The stator winding flux

此外，撬棒电阻的引入虽然导致定子绕组磁链暂态特性变得极为复杂，但是定子绕组磁链的稳态特性则不受撬棒电阻的影响，即式（15）中的定子绕组磁链的稳态分量是准确的。

4 电网故障情况下DFIG定子电流特性

4.1 理论分析

由式（4）可得

撬棒保护动作后，转子绕组端电压为零，即

将式（16）、式（17）和式（18）代入式（3）后可得

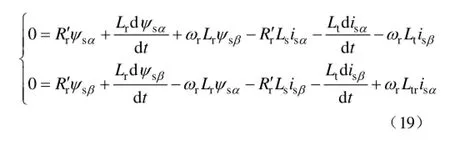
对式（19）进行求解可以得到定子电流为

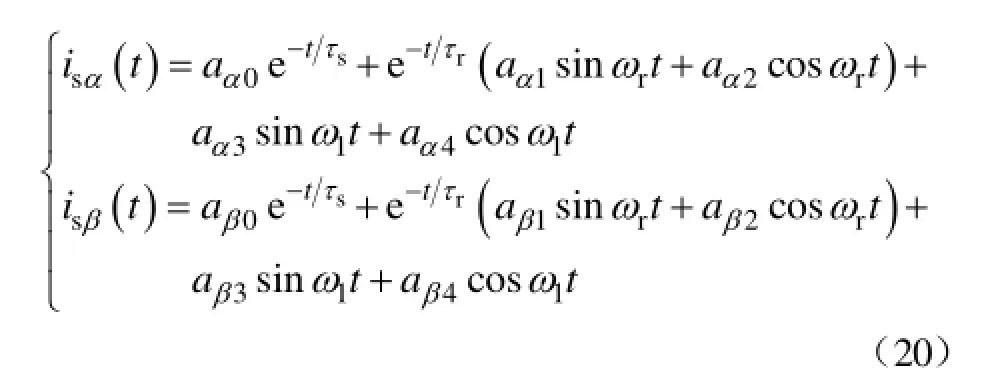
对式（20）进行坐标变换即可得到定子三相电流。从中可以看出，为了保证在撬棒保护动作瞬间定子绕组磁链维持守恒，定子电流中含有直流分量。同样地，为了维持转子绕组磁链初值不变，转子电流中将出现直流分量，且该电流产生的磁链相对定子以转速ωr旋转。为了抵消这个交变磁链，定子电流中将出现角频率为ωr的电流。这与传统同步发电机故障电流中含有基频自由分量不同。

定子电流中的直流分量和角频率为ωr的电流分量均是衰减的，其初始大小均与故障发生时刻、故障后的电压幅值和 DFIG转子旋转速度有关。除了含有衰减的直流分量和角频率为ωr的电流外，定子电流中还含有稳态基频分量。该基频分量的大小与故障后的电压幅值和 DFIG转子旋转速度有关。

此外，由于式（15）中的定子绕组磁链的稳态分量是准确的，则根据定子绕组磁链的简化模型计算得到的定子故障电流的稳态基频分量的幅值也是准确的，即式（20）中的稳态基频分量可以准确反映实际故障情况下定子故障电流的稳态特性。

4.2 仿真验证

为了验证上述分析结果，在PSCAD/EMTDC仿真平台上搭建了 DFIG的仿真模型，并针对三相电压跌落和 BC两相电压跌落两种故障情况下 DFIG定子电流进行了仿真分析。DFIG的参数见附录A。

本文对不同电压跌落深度下 DFIG的故障电流特性进行了仿真验证，但是限于篇幅，仅给了电压跌落至0.2(pu)情况下DFIG故障电流的仿真算例。其中，图 3给出了三相电压对称跌落至 0.2(pu)时DFIG定子三相电流仿真波形与理论波形的对比；图4给出了BC两相电压跌落至0.2(pu)时DFIG定子三相电流仿真波形与理论波形的对比。此外，故障发生前 DFIG处于额定运行状态，转子转速为 1.2 (pu)，即。

图3 三相电压对称跌落至0.2(pu)时DFIG定子电流Fig.3 The stator currents for three-phase voltage dips

图4 BC两相电压跌落至0.2(pu)时DFIG定子电流Fig.4 The stator currents for two-phase voltage dips

由上可知，虽然由于撬棒电阻的引入，定、转子绕组之间的耦合显著增强，给 DFIG定子电流故障特性的分析带来了复杂度，但基于本文提出的定子绕组磁链简化计算模型得到的 DFIG定子故障电流在前2个工频周期内仍具有较高的准确度。当定子电流中的暂态分量完全衰减之后，由式（20）计算得到的定子电流的稳态基频分量的波形与仿真波形完全吻合，验证了上述理论分析结果。

根据继电保护原理研究和整定计算的应用要求，暂态过程中故障电流最大值和稳态故障电流值是两个极为重要的参数。而本文得到的电网故障情况下的定子电流解析表达式在故障发生后的前2个工频周期内和故障稳态期间均具有较高的准确度。这保证了通常在故障发生后第一个工频周期内出现的最大故障电流和稳态故障电流的计算的精确性。仿真分析结果则验证了上述结论的正确性。因此，基于本文提出的定子绕组磁链简化计算模型得到的定子故障电流解析表达式能够满足电网继电保护原理研究和整定计算的应用要求。

值得注意的是，以上的分析未对电网电压做任何近似和假设，因此，上述结论对于任何形式的电网故障都是成立的。

5 DFIG定子故障电流等效计算模型

在上述分析的基础上，对电网故障情况下 DFIG定子绕组电流的等效计算模型开展进一步的研究。一方面，定子故障电流中的衰减直流分量将被滤除，对保护装置的影响较小；另一方面，由于运行过程中要求DFIG的转差率在±0.3之间，导致定子故障电流衰减交流分量的频率处于 35～65Hz之间，难以滤除，从而对继电保护装置带来较大的影响。因此，本文主要针对 DFIG定子电流中的稳态基频电流分量和角频率为ωr的衰减电流分量进行分析。

5.1 稳态基频电流分量

由式（20）可知，在两相静止坐标系下定子故障电流基频分量为

因此，可以得到三相定子故障电流的基频分量为

以机端单相接地短路为例进行分析。当机端发生A相接地故障时，各相电压及A相正、负序电压分别为

对式（23）进行坐标变换，得到两相静止坐标

下的定子电压为

将附录B中的系数代入式（22），并结合式（25）求得定子A相基频电流正、负序分量为

由此可以得到A相正、负序分量等效计算模型如图5所示。

图5 A相电流正、负序分量等效计算模型Fig.5 The equivalent calculation models for sequence components of Phase A current

从图 5可以看出，实际上，DFIG稳态基频电流分量的等效计算模型即为异步电动机的等效模型，同时验证了上述理论分析结果的正确性。

5.2 角频率为ωr的衰减电流分量

由式（20）可知，在两相静止坐标系下定子电流中角频率为ωr的暂态分量电流为

因此，可以得到三相定子中角频率为ωr的暂态分量电流为

将附录 B中的系数代入式（25），求得定子 A相电流中角频率为ωr的暂态分量电流的正、负序分量为

从式（28）可以看出，即使在单相接地故障情况下，角频率为ωr的暂态电流分量中只存在正序电流，而无负序电流。这是因为在故障发生瞬间，为了维持转子绕组磁链初值不变，转子绕组磁链中将出现直流分量。该直流分量产生的转子绕组磁链相对转子静止，相对定子以ωr的角速度旋转。因此，转子绕组中的直流分量将在定子绕组中感应出角频率为ωr的交流电流分量，且该交流电流中只含有正序分量。

根据式（29）及附录C中的相关系数，可将定子 A 相电流中角频率为ωr的暂态分量电流分为与撬棒保护动作前状态有关的电流分量和与故障后机端电压有关的电流分量和两种类型。

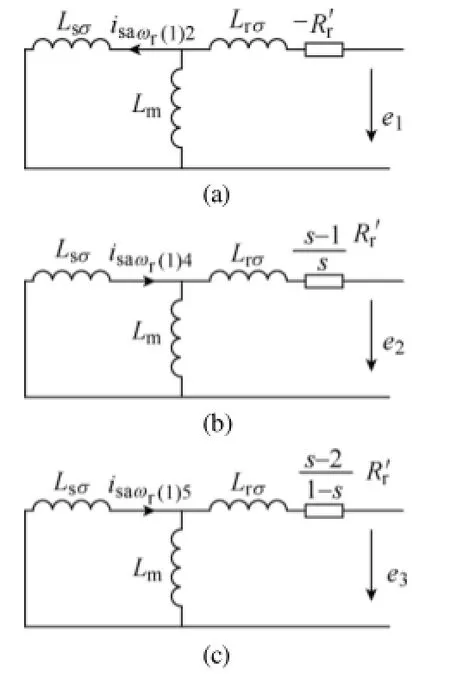
图6 各电流分量的等效计算模型Fig.6 The equivalent calculation models for current components

从式（28）及图6可以看出，角频率为ωr的电流分量的计算实际上是独立于外部电路的。通过对基频电流分量网络的计算得到 DFIG机端三相电压之后，即可以通过式（28）或图6计算得到角频率为ωr的电流分量。

图5及图6给出的DFIG定子故障电流各交流分量的等效计算模型均从式（20）中直接推导得到，上一节的仿真分析可以验证其准确性。此外，通过上述等效计算模型，可以建立含 DFIG的电网故障分析理论和方法。篇幅所限，本文不对此进行深入的研究和阐述。

6 结论

结合 DFIG的结构和运行特点，为了适应不同电网故障情况下 DFIG故障电流特性分析的需要，本文建立了两相静止坐标系下 DFIG的电磁暂态方程。以此为基础，对撬棒保护动作情况下 DFIG定子绕组磁链和定子电流故障特性进行了研究，得到了DFIG定子故障电流各分量的等效计算模型。

（1）撬棒电阻的引入使得定、转子绕组磁链之间的耦合显著增强，定子绕组磁链的暂态特性极其复杂。本文提出了一种定子绕组磁链的简化计算模型，可以较为准确地反应撬棒保护动作后的前4个工频周期内及稳态时的定子绕组磁链。

（2）基于定子绕组磁链的简化计算模型，得到各种电网故障情况下定子电流的表达式。仿真证明理论得到的定子电流表达式在前2个工频周期和稳态阶段具有很高的准确度，能够满足继电保护原理研究和整定计算的应用要求。

（3）撬棒保护动作后，DFIG定子电流中除含有稳态基频分量和衰减直流分量外，还有角频率为ωr的衰减电流分量。这与传统同步发电机故障电流中含有稳态基频分量、衰减直流分量和基频自由分量的故障特征不同。

（4）DFIG稳态基频电流分量的等效计算模型即为异步电动机的等效模型。此外，无论是对称故障还是不对称故障，角频率为ωr的衰减电流分量中只存在正序电流，而无负序电流。

本文的研究结果对于研究适用于含 DFIG的电网新型继电保护原理和整定计算原则具有重要的理论意义。

附录A

模型中 DFIG的参数如下：额定容量：1.5MV·A；额定线电压：690V；定子绕组电阻：0.007 56（pu）；定子漏电抗：0.142 5（pu）；转子绕组电阻：0.005 33（pu）；转子漏电抗：0.142 5（pu）；定转子互感：2.176 7（pu）；转子额定转速：1.2（pu）。

附录B

其中，isα0、isβ0、ψsα0和ψsβ0分别表示撬棒保护动作瞬刻定子电流、磁链在两相静止坐标系下的分量的初始值。

附录C

[1] 刘其辉, 谢孟丽. 双馈式变速恒频风力发电机的空载及负载并网策略[J]. 电工技术学报, 2012, 27(10): 60-67, 78.

Liu Qihui, Xie Mengli. Strategies of grid-connection of doubly-fed variable-speed constant-frequency wind power generator with no-load and with load[J]. Transactions of China Electrotechnical Society, 2012, 27(10): 60-67, 78.

[2] Muller S, Deicke M, De Doncker R W. Doubly fed induction generator systems for wind turbines[J]. IEEE Industry Applications Magazine, 2002, 8(3): 26-33.

[3] Hughes F M, Lara O A, Jenkins N, et al. Control of DFIG-based wind generation for power network support [J]. IEEE Transaction on Power Systems, 2005, 20(4): 1958-1966.

[4] 贺益康, 周鹏. 变速恒频双馈异步风力发电系统低电压穿越技术综述[J]. 电工技术学报, 2009, 24(9): 140-146.

He Yikang, Zhou Peng. Overview of the low voltage ride-through technology for variable speed constant frequency doubly fed wind power generation systems [J]. Transactions of China Electrotechnical Society, 2009, 24(9): 140-146.

[5] 叶希, 鲁宗相, 乔颖, 等. 大规模风电机组连锁脱网事故机理初探[J]. 电力系统自动化, 2012, 36(8): 11-17.

Ye Xi, Lu Zongxiang, Qiao Yin, et al. A primary analysis on mechanism of large scale cascading tripoff of wind turbine generators[J]. Automation of Electric Power Systems, 2012, 36(8): 11-17.

[6] 雷亚洲, Gordon Lightbody. 国外风力发电导则及动态模型简介[J]. 电网技术, 2005, 25(12): 27-32.

Lei Yazhou, Gordon Lightbody. An introduction on wind power grid code and dynamic simulation[J]. Power System Technology, 2005, 25(12): 27-32.

[7] Tsili M, Papathanassiou S. A review of grid code technical requirements for wind farms[J]. IET Renewable Power Generation, 2009, 3(3): 308-332.

[8] 撖奥洋, 张哲, 尹项根, 等. 双馈风力发电系统故障特性及保护方案构建[J]. 电工技术学报, 2012, 27(4): 233-239.

Han Aoyang, Zhang Zhe, Yin Xianggen, et al. Research on fault characteristic and grid connecting-point protection scheme for wind power generation with doublyfed induction generator[J]. Transactions of China Electrotechnical Society, 2012, 27(4): 233-239.

[9] Morren J, de Haan S W H. Ridethrough of windturbines with doubly-fed induction generator during a voltage dip[J]. IEEE Transaction on Energy Conversion, 2005, 20(1): 435-441.

[10] 关宏亮, 赵海翔, 王伟胜, 等. 风电机组低电压穿越功能及其应用[J]. 电工技术学报, 2007, 22(10): 173-177.

Guan Hongliang, Zhao Haixiang, Wang Weisheng, et al. LVRT capability of wind turbine generator and its application[J]. Transactions of China Electrotechnical Society, 2007, 22(10): 173-177.

[11] 周宏林, 杨耕. 不同电压跌落深度下基于撬棒保护的双馈式风机短路电流特性分析[J]. 中国电机工程学报, 2009, 29(S1): 184-191.

Zhou Honglin, Yang Gen. Short circuit current characteristics of doubly fed induction generator with crowbar protection under different voltage dips[J]. Proceedings of the CSEE, 2009, 29(S1): 184-191.

[12] Vicatos M S, Tegopoulos J A. Transient state analysis of a doubly-fed induction generator under three phase short circuit[J]. IEEE Transactions on Energy Conversion, 1991, 6(1): 62-68.

[13] Morren J, de Haan S W H. Short-circuit current of wind turbines with doubly-fed induction generator[J]. IEEE Transactions on Energy Conversion, 2007, 22(1): 174-180.

[14] 吕志强, 许国东. 兆瓦级双馈风电机组电网故障时的暂态分析[J]. 电力系统保护与控制, 2010, 38(23): 112-116, 125.

Lü Zhiqiang, Xu Guodong. Transient analysis of grid short circuit fault of megawatt doubly fed wind turbine [J]. Power System Protection and Control, 2010, 38(23): 112-116, 125.

[15] 张建华, 陈星莺, 刘皓明, 等. 双馈风力发电机三相短路分析及短路器最大电阻整定[J]. 电力自动化设备, 2009, 29(4): 6-10.

Zhang Jianhua, Chen Xingying, Liu Haoming, et al. There-phase short-circuit analysis for double-fed winddriven generator and short-circuit maximal resistance calculation[J]. Electric Power Automation Equipment, 2009, 29(4): 6-10.

[16] 翟佳俊, 张步涵, 谢光龙, 等. 基于撬棒保护的双馈风电机组三相对称短路电流特性[J]. 电力系统自动化, 2013, 37(3): 18-23.

Zhai Jiajun, Zhang Buhan, Xie Guanglong, et al. Threephase symmetrical short-circuit current characteristics analysis of wind turbine driven DFIG with crowbar protection[J]. Automation of Electric Power Systems, 2013, 37(3): 18-23.

[17] 胡家兵, 贺益康, 郭晓明, 等. 不平衡电压下双馈异步风力发电系统的建模与控制[J]. 电力系统自动化, 2007, 31(14): 47-56.

Hu Jiabing, He Yikang, Guo Xiaoming, et al. Modeling and control of the DFIG based wind-power generation system under unbalanced grid voltage conditions[J]. Automation of Electric Power Systems, 2007, 31(14): 47-56.

Study of Fault Current Characteristics of DFIG Considering Impact of Crowbar Protection

Kong Xiangping Zhang Zhe Yin Xianggen Wang Fei Long Mao

（State Key Laboratory of Advanced Electromagnetic Engineering and Technology Huazhong University of Science and Technology Wuhan 430074 China）

In order to study the fault current characteristics of doubly-fed induction generator (DFIG) under symmetrical and asymmetrical fault conditions, dynamic model of DFIG in stator stationary reference frame is developed. On condition that a severe fault occurs and crowbar protection is activated, the dynamic characteristics of stator flux linkage of DFIG are studied. Moreover, a simplified calculation model of stator flux linkage is established with consideration of accuracy as well as simplicity. Based on it, the fault current characteristics DFIG under cond itions of symmetrical faults and asymmetrical faults are analyzed and the analytical expressions are obtained. Besides, the equivalent calculation models of fault current are built. Finally, the digital simulation results show that the theoretical analysis results have high accuracy in the first two cycles after the fault occurs which can meet the requirements of the study of relaying protection principle and setting calculation.

Doubly-fed induction generator(DFIG), crowbar protection, stator flux linkage, fault current characteristics, equivalent calculation model

TM315

孔祥平 男，1988年生，博士研究生，主要研究方向为应对分布式电源大规模接入的电力系统继电保护及安全稳定控制。

国家自然科学基金资助项目（51177058，51077061）。

2013-06-25 改稿日期 2013-12-27

张 哲 男，1962生，教授，博士生导师，主要研究方向为电力系统继电保护、新能源及超导技术。