多种不确定性并存情形下的非常规可靠性度量方法

李玲玲 段超颖 李志刚

多种不确定性并存情形下的非常规可靠性度量方法

李玲玲 段超颖 李志刚

（河北工业大学电磁场与电器可靠性省部共建重点实验室 天津 300130）

多种不确定性（如随机性、模糊性和不完全可信性）并存的情形在现实中很常见，但此情形下的可靠性度量并未得到充分研究。本文基于模糊理论和云理论提出了一种适用于上述情形的可靠性度量方法，即：首先针对应力、强度中的模糊变量，根据其不完全可信性采用云理论对其隶属函数进行云化处理，并在不同可信度下获得以上、下隶属函数描述的正态云生成区间值Fuzzy集；然后对上、下隶属函数进行处理，使其拥有概率密度函数的数学特征，进而采用常规的应力-强度干涉模型计算可靠度的上、下限，构造一个可靠度区间，最终获得一条由一系列可靠度区间及其相应的可信度构造的分布曲线，以此作为可靠性度量结果。本文方法不仅可综合处理多种不确定性，且能使更多信息保留在可靠性度量结果中。

可靠性度量 随机性 模糊性 不完全可信性 区间值 Fuzzy集 正态云

1 引言

常规的可靠性理论以概率论和数理统计为基础，称为概率可靠性模型[1-2]，但是它只研究工程设计中存在的随机现象，仅能处理随机性而不能处理模糊性、不完全可信性等其他类型的不确定性（所谓不完全可信性，是指人们对相关信息并不完全信任），因此模糊可靠性[3]、能度可靠性、稳健可靠性以及在稳健可靠性基础上发展起来的区间可靠性[4]等相继被提出，然而这些方法在综合处理多种不确定性方面仍存在一定局限性。局限性一方面表现在上述方法只针对一种或两种不确定性，如以模糊概率公式或截集概念为基础的模糊可靠性只是探讨变量的随机性和模糊性对可靠度的影响；另一方面表现在可靠性的度量结果上，只用单一值或者区间值表示度量结果并不完善，不能够满足工程师快速查找可靠度的需求。当前，将人工智能、计算智能方法[5-8]引入可靠性工程以解决并存于实际问题中的各种不确定因素是一种新的发展趋势，文献[9-10]分别提出了一种基于D-S证据理论的系统可靠性分析、评估方法，但是应用证据理论的算法是一个独立系统，并不能得到常规可靠性与模糊可靠性的联系；文献[11]提出了一种基于云理论、可处理多种不确定性的可靠性度量模型，但其可靠性度量结果被表达为一种云分布，实用性较差，不利于为实际问题的解决提供直接指导。

针对这种情况，本文提出一种旨在同时处理随机性、模糊性和不完全可信性的非常规可靠性度量方法，即基于正态云生成区间值Fuzzy集方法。该方法可以获得可靠度可信度曲线，适用于已知应力、强度分布或通过计算可以获得其分布的精密产品的可靠性度量，不仅使度量结果蕴含了比现有方法更多的信息，而且克服了文献[11]方法“实用性差”的不足。

2 基础知识简介

2.1 模糊可靠度计算模型

文献[12]提出了一种综合处理随机不确定信息与模糊不确定信息的可靠度计算方法。该方法在应力、强度为随机变量、模糊变量的任意组合下都具有可用性，其特点是首先处理应力、强度中的模糊变量，使之具有与随机变量相同的数学性质；然后借助应力—强度干涉模型获得一个以分布函数（分布曲线）表达的可靠度度量结果，从而建立起一个可同时处理随机性与模糊性的可靠度计算模型。以下对文献[12]中可靠度计算方法做一简单说明。

（1）当应力、强度变量均为随机变量时，应用传统可靠性理论中经典的应力—强度干涉模型进行可靠度求解。应力-强度干涉模型如图1所示。

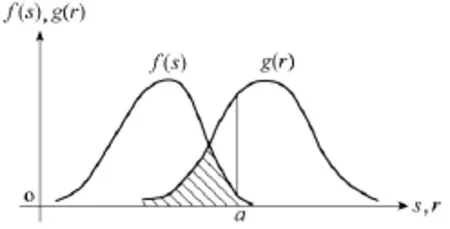
图1 应力-强度干涉模型Fig.1 Stress-intensity interference model

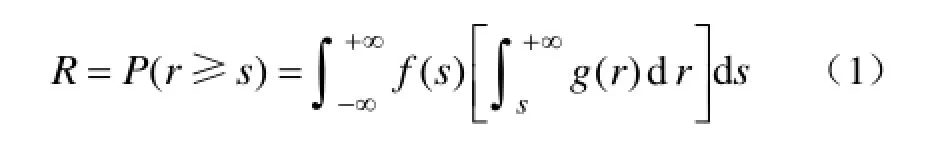
在论域U范围内，常规可靠性理论中可靠度R计算式为式中，f(s)、g(r)分别为随机应力、随机强度的概率密度函数。

当s=r=a时，给出强度一定时产品安全程度和应力一定时产品安全程度的定义，分别用字母表示为P、Q，并有

所以，可以将常规可靠度计算式（1）表示为

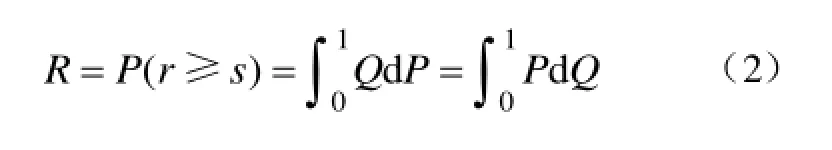
若令P为x轴，Q为y轴，当a在U上自由取值、并遍历 U时，即获得了无数个序偶（P, Q），则可以得到一条表征产品可靠度的曲线，如图 2所示，曲线与x轴、y轴所围面积即为产品可靠度值。

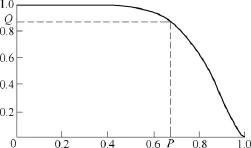
图2 可靠度分布曲线Fig.2 The reliability distribution curve

（2）当应力、强度变量其中一个为模糊变量或者两者均为模糊变量时，首先对模糊变量的隶属函数进行转换，将其转换为具有概率密度函数性质的函数；再将转换好的函数带入常规可靠性计算方法中计算。

假设模糊变量的隶属函数为μU(x)，转换过程按式（3）进行处理。

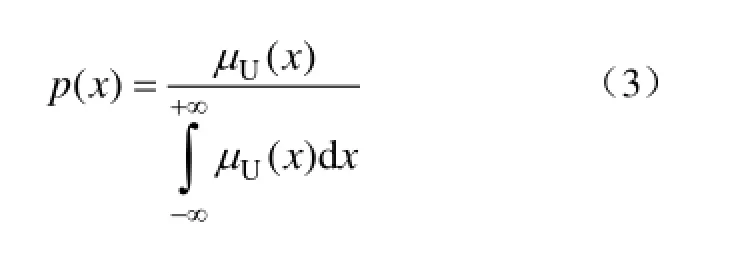
p(x)便成为了具有概率密度函数性质的函数，称这个过程为归一化处理，称p(x)为归一化函数，此后可以按式（1）计算模糊可靠度。

2.2 云滴贡献度

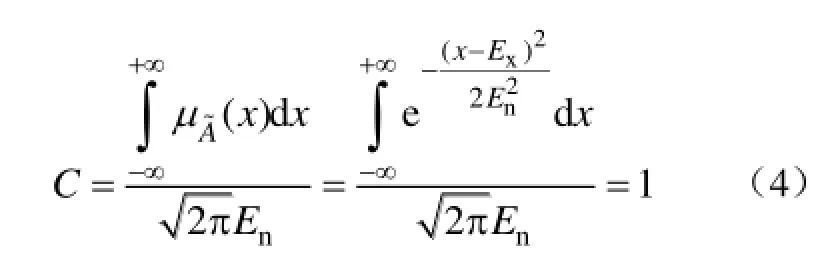
当超熵He=0时，云滴分布为高斯分布，此时所有云滴都分布在高斯曲线上。随着超熵 He逐渐增大，云滴开始离散，当En-3He＞0时，有99.74%的云滴落在曲线 y1和 y2所围的区域内，其中，如图3所示。这就是正态云“熵的 3σ准则”。

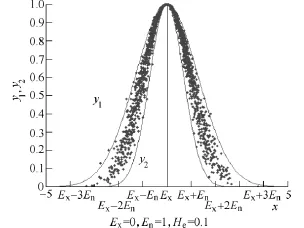
图3 熵的3σ准则Fig.3 The 3σ criterion of Entropy

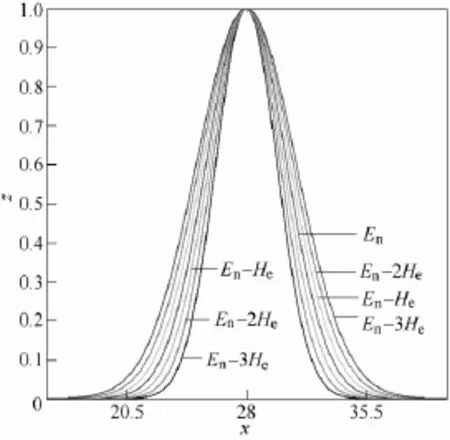
图4 超熵的3σ准则Fig.4 The 3σ criterion of Hyper entropy

表1列出了熵和超熵的三个特殊倍数时对应的云滴贡献度。同样，可以根据式（4）计算熵和超熵任意倍数时对应的云滴贡献度。

表1 云滴定性贡献Tab.1 Qualitative contribution of cloud droplets

2.3 正态云生成区间值Fuzzy集

根据区间值Fuzzy集理论以及云滴对定性概念的贡献度，给出正态云生成区间值 Fuzzy集的定义[18]。

设 C是论域 U上的定性概念，其正态云的数字特征为(Ex, En, He)，令，其中，，则称为正态云生成的一个区间值Fuzzy集。该定义说明由云滴产生的随机数主要（99.74%）落在区间值Fuzzy集C的值域带子里。根据正态云生成区间值Fuzzy集定义和表 1的内容，可以得出一个衍生概念，n倍正态云生成区间值 Fuzzy集。在正态云生成区间值 Fuzzy集定义中，令，其中，且。称为n倍正态云生成的区间值Fuzzy集。

该衍生定义与原始定义最主要的区别是将3倍超熵扩展成为[0,3]区间上任意实数倍数的超熵，当取定一个超熵倍数n时，同样可以求得云滴贡献度C来表征云滴产生的随机数落在区间值Fuzzy集的值域带内的概率，此时，每一个n值都对应一个可信度。可信度T满足，。比如当n=0时，和相同，均为该云模型的期望曲线，强度的区间值Fuzzy集成为了对应的隶属函数曲线，即只考虑到了模糊性的曲线，这样就违背了考虑随机性、模糊性和不完全可信性这三种不确定性的初衷，所以认为其可信度 T=0、n=3时，应力和强度的区间值Fuzzy集曲线值域带子很宽，即云模型的厚度较大，不完全可信性取值较大，此时对应的云滴贡献度虽然很高，但其可信度 T= 0.002 7。图5展示了当n=1时，有68.26%的云滴落在区间值Fuzzy集的值域带里，其余云滴落在值域带外。

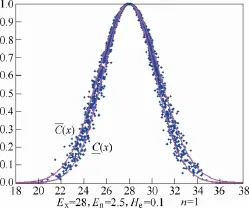
图5 1倍正态云生成区间值Fuzzy集Fig.5 One times Gaussian cloud formed interval-valued Fuzzy set model

3 模型建立及算例分析

直流电机的电磁转矩受电枢绕组上的电枢电流影响，针对电机转矩的可靠性能进行分析，假设电流应力变化范围，电流强度变化范围。设该型号产品应力变量为随机变量，且符合正态分布，，强度为模糊变量，其模糊隶属函数为。根据以上信息建立随机应力-模糊强度的可靠性度量模型。

在该算例中，应力为随机变量不作处理，将模糊强度变量根据其不完全可信性采用云理论对其隶属函数进行云化处理，并在不同可信度下获得以上、下隶属函数描述的正态云生成区间值Fuzzy集；然后对强度变量的上、下隶属函数进行处理，使其拥有概率密度函数的数学特征，进而采用常规的应力-强度干涉模型计算随机应力、模糊强度模型可靠度的上、下限，构造一个可靠度区间，最终获得一条由一系列可靠度区间及其相应的可信度构造的分布曲线，以此作为可靠性度量结果。

3.1 建立 3倍正态云生成区间值 Fuzzy集

算例中，应力变量为随机变量而且概率密度函数已知，就不再做处理；如果针对强度变量源信息可信度为0.9，则强度云模型中的超熵对强度变量建立 3倍正态云生成区间值 Fuzzy集模型，此时 99.74%的云滴落在区间带子内，模型为

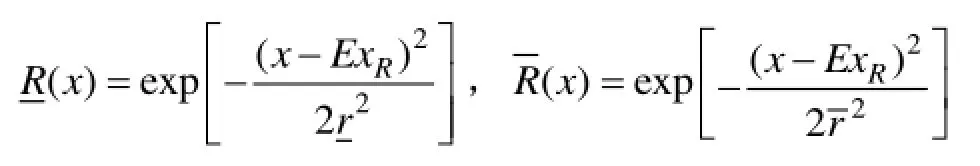
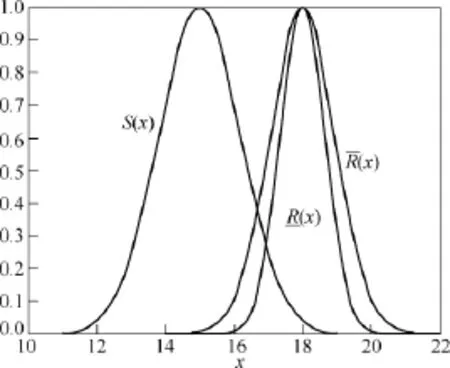
图6 应力-强度区间值Fuzzy集Fig.6 Stress-intensity interval-valued Fuzzy set model

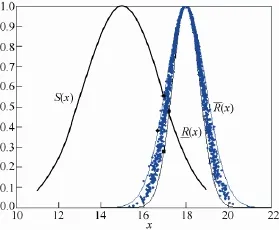
图7 3倍正态云生成应力-强度区间值Fuzzy集Fig.7 Three times Gaussian cloud formed interval-valued Fuzzy set model of stress-intensity model

3.2 模糊可靠度计算

由于强度变量的隶属函数是基于区间值 Fuzzy集的，即分别拥有上、下两个隶属函数，以上文中提到的归一化模糊可靠度计算方法为基础，根据式（4），针对不同的强度隶属函数会有不同的可靠度解，所以，对于可靠度的求解会有两种不同的组合方式：①随机应力和模糊强度的下隶属函数组合；②随机应力和模糊强度的上隶属函数组合。以组合①为例说明模糊可靠度的求解过程。

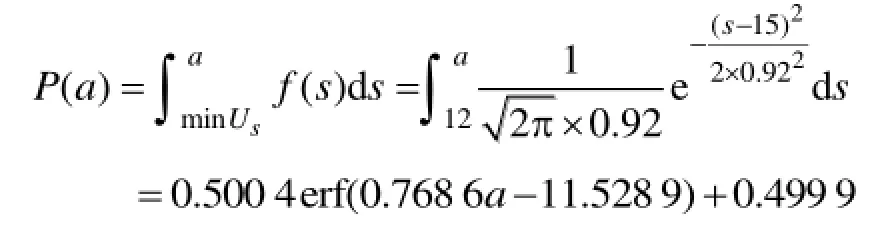
强度模糊变量的下隶属函数为

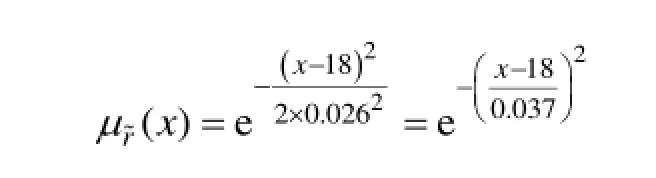
同时，应力一定时产品安全程度Q为

其中，erf(x)函数为误差函数，是对一个形如正态分布的概率密度函数利用Matlab计算变上限积分的结果；。

根据应力、强度的安全概率密度函数 P(l)和Q(l)，可以得到部分P、Q的值，见表2。

表2 部分P、Q值Tab.2 A part of numerical values of P、Q

通过仿真计算，得到更多 P、Q值，绘制成模糊可靠度分布曲线，如图 8所示。

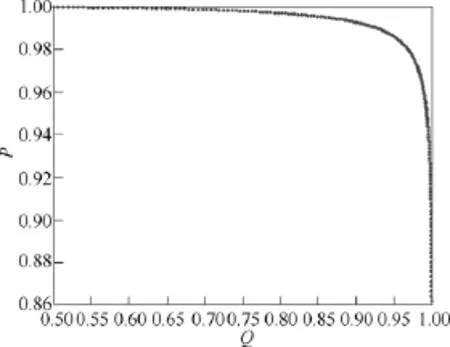
图8 可靠度分布曲线Fig.8 The reliability distribution curve

再根据式（4）可以算出模糊可靠度为

按照上述计算原理，对强度变量分别建立n倍正态云生成区间值Fuzzy集且），同时求出对应的云滴贡献度。应用 Matlab编程可以分别得到n倍正态云生成区间值 Fuzzy集时，继电器对应的模糊可靠度区间、贡献度及可信度，表3列举了几个特殊倍数时对应的数据。

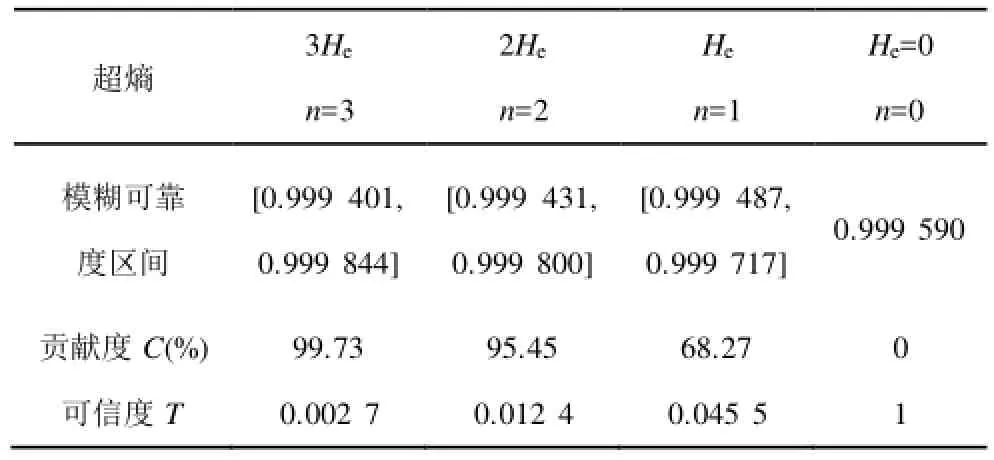
表3 n倍正态云生成区间值Fuzzy集对应的模糊可靠度区间和贡献度Tab.3 Fuzzy reliability intervals and contributions of n times Gaussian cloud formed interval-valued Fuzzy set model of stress-intensity model

图9将表3中列举的数据绘制成了可靠度可信度分布散点图。

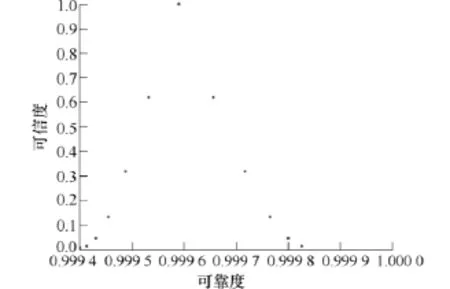
图9 可靠度-可信度的分布Fig.9 The reliability-credibility distribution

保持超熵不变即He=0.1时，改变n的数值建立应力-强度n倍正态云生成区间值Fuzzy集，进而获得更多模糊可靠度区间-可信度的数据，图 10表示n以0.01为步长变化时获得的可靠度-可信度分布。

文献[11]提出了可信度的概念，并绘制了可靠度-可信度分布曲线，用来表征“对象的可靠性度量值在某种程度上是值得相信的”这个概念的可信程度。图 10所示可靠度-可信度曲线，得到了和文献[11]类似的结果。

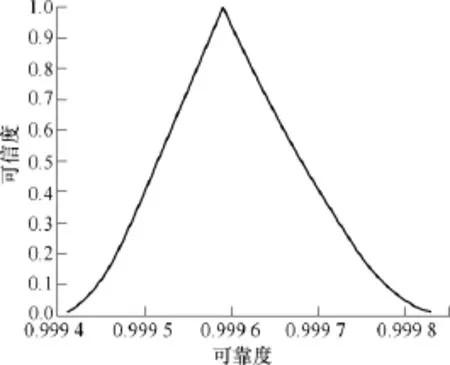
图10 步长为0.01时可靠度-可信度分布Fig.10 The reliability-credibility distribution when step is 0.01

以图10例均为He=0.1情况下取不同步长时的可靠度-可信度曲线；当超熵变化时，即对模糊变量（本文指强度）的不完全可信性取值变化时，获得的可靠度-可信度分布曲线，如图 11所示，两条曲线说明了超熵的大小对可靠度的影响。可见，超熵的变化并不影响可信度为1时的可靠度取值，只是改变了可靠度-可信度的分布形式。

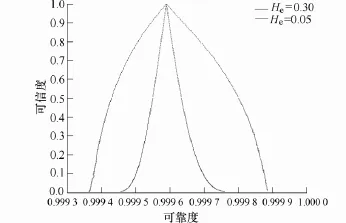
图11 He=0.05时可靠度-可信度的分布Fig.11 The reliability-credibility distribution with different Hyper entropys

3.3 继电器温度实例

某型号继电器温度的变化范围为-40～70℃，认为此区间为温度强度区间，若温度应力的变化范围为-60～40℃，假设其温度应力和温度强度均为模糊变量，且隶属函数如下，取超熵为 0.1时，云化的区间值Fuzzy集模型如图 12所示。

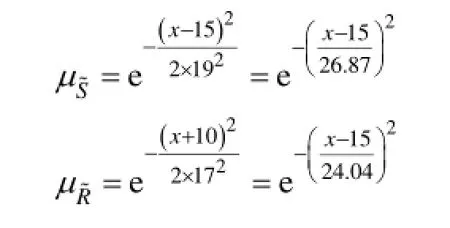
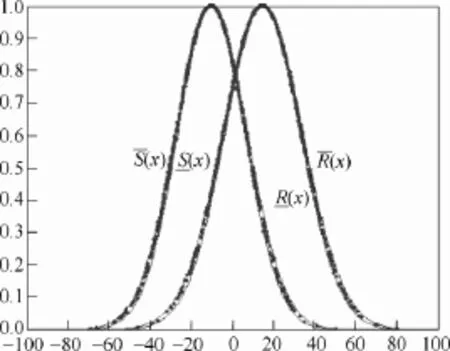
图12 3倍正态云生成应力-强度区间值Fuzzy集Fig.12 Three times Gaussian cloud formed interval-valued Fuzzy set model of stress-intensity model

由图 12可以看出应力与强度干涉区域较大，根据式（2）可以计算出模糊可靠度为=0.685，图 13为步长为0.1，超熵为0.1时获得的继电器温度应力强度的可靠度可信度分布图，由图 13中可以读出可靠度为0.685时对应的可信度为1，与计算结果相符。

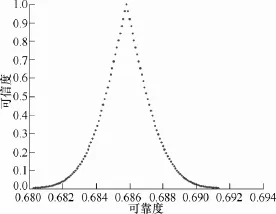
图13 步长为0.1时可靠度-可信度分布Fig.13 The reliability-credibility distribution when step is 0.1

由图 13可以看出继电器温度为例，可靠度在[0.68,0.69]区间范围内变化，可靠性能较低。同样可以得出超熵为 0.1，步长为 0.01时可靠度可信度分布曲线，如图 14所示。

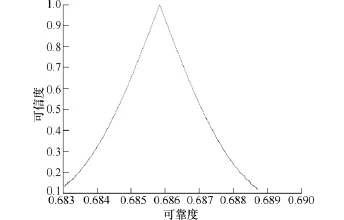
图14 步长为0.01时可靠度-可信度分布Fig.14 The reliability-credibility distribution when step is 0.01

4 结论

在常规的可靠性分析中，除了随机不确定信息和模糊不确定信息，通常还需要处理不完全可信的不确定信息，为此，本文提出了基于正态云生成的区间值Fuzzy集模型，能够同时处理上述不确定性，并得出如下结论，该可靠性度量模型适用于应力、强度变量为随机或模糊的任意组合，可以应用到机械、电器产品的可靠性度量中，由于获得的模糊可靠度精度较高，该模型尤其适用于对于可靠性要求较高的领域中。

（1）不完全可信性则存在于对源信息的可靠性的信任程度以及对于同一概念的不同认知。利用正态云的超熵来考虑源信息的不完全可信性解决了对第三种不确定性的处理。

（2）对于含有模糊信息的变量，对变量建立区间值Fuzzy集，利用其上、下隶属函数计算模糊可靠度，并用区间表示，这个过程考虑了变量的模糊性；而且利用云模型对区间值Fuzzy集进行云化，将云滴的随机性与模糊性融合了起来。

（3）可靠性度量结果以一条由一系列可靠度区间及其相应的可信度构造的分布曲线来表示，由结果中不仅可以看出可靠度的趋势，读出某可靠度区间及其对应的可信度，还可以绘制不同超熵情况下的可靠度曲线。

[1] 张明朗. 浅析概率可靠性模型的优缺点[J]. 兰州工业高等专科学校学报, 2010, 17(2): 39-41.

Zhang Minglang. Analysis of advantages and disadvantages of probabilistic reliability model[J]. Journal of Lan Zhou Polytechnic College, 2010, 17(2): 39-41.

[2] Qiu Z, Wang J. The interval estimation of reliability for probabilistic and non-probabilistic hybrid structural system[J]. Engineering Failure Analysis, 2010, 17(5): 1142-1154.

[3] Li Zhigang, Li Lingling, Zhu Fenfen, et al. A new algorithm of closeness degree for fuzzy pattern recognition[J]. International Journal of Intelligent Engineering & Systems, 2010, 3(4): 9-16.

[4] 李玲玲, 周贤, 张云龙, 等. 基于区间分析的继电器稳健可靠性研究[J]. 低压电器, 2012(22): 4-7.

Li Lingling, Zhou Xian, Zhang Yunlong, et al. Study on the relay’s robust reliability based on interval analysis[J]. Low Voltage Apparatus, 2012(22): 4-7.

[5] 李志刚, 李玲玲. 串联系统的可靠性评估方法研究[J]. 电工技术学报, 2011, 26(1): 146-153.

Li Zhigang, Li Lingling. A method of evaluating the reliability of series systems[J]. Transactions of China Electrotechnical Society, 2011, 26(1): 146-153.

[6] 张镱议, 廖瑞金, 杨丽君. 基于云理论的电力变压器绝缘状态评估方法[J]. 电工技术学报, 2012, 27(5): 13-20.

Zhang Yiyi, Liao Ruijin, Yang Lijun, et al. An assessment method for insulation condition of power transformer based upon cloud model[J]. Transactions of China Electrotechnical Society, 2012, 27(5): 13-20.

[7] 张智锐, 肖繁, 焦邵麟, 等. 不同过程层网络结构的保护系统可靠性分析[J]. 电力系统保护与控制, 2013, 41(18): 142-148.

Zhang Zhirui, Xiao Fan, Jiao Shaolin, et al. Reliability evaluation of protective relay system based on process layer network[J]. Power System Protection and Control, 2013, 41(18): 142-148.

[8] 戴志辉, 王增平, 焦彦军, 等. 基于缺陷分析的保护装置可靠性评价研究[J]. 电力系统保护与控制, 2013, 41(12): 54-59.

Dai Zhihui, Wang Zengping, Jiao Yanjun, et al. Study on the reliability evaluation of protection devices based on defects analysis[J]. Power System Protection and Control, 2013, 41(12): 54-59.

[9] 赵书强, 程德才, 刘璐. 结合 D-S证据推理的贝叶斯网络法在配电网可靠性评估中的应用[J]. 电工技术学报, 2009, 24(7): 134-138.

Zhao Shuqiang, Cheng Decai, Liu Lu. Reliability evaluation of power distribution system based on D-S evidence inference and bayesian networks method[J]. Transactions of China Electrotechnical Society, 2009, 24(7): 134-138.

[10] 姜潮, 张哲, 韩旭, 等. 一种基于证据理论的结构可靠性分析方法[J]. 力学学报, 2013, 45(1): 103-115.

Jiang Chao, Zhang Zhe, Han Xu, et al. An evidence theory based reliability analysis method for uncertain ctructures[J]. Chinese Journal of Theoretical and Applied Mechanics, 2013, 45 (1): 103-115.

[11] 李玲玲, 朱芬芬, 姚致清, 等. 基于可信度的可靠性度量云模型[J]. 电力系统保护与控制, 2012, 40(8): 90-94.

Li Lingling, Zhu Fenfen, Yao Zhiqing. Reliability measure cloud model based on credibility[J]. Power System Protection and Control, 2012, 40(8): 90-94.

[12] 李玲玲, 武猛, 景丽婷, 等. 可靠性分析中的模糊信息处理方法[J]. 模糊系统与数学, 2011, 25(5): 90-95.

Li Lingling, Wu Meng, Jing Liting, et al. Fuzzy information processing method in reliability analysis [J]. Fuzzy Systems and Mathematics, 2011, 25(5): 90-95.

[13] 王国胤. 云模型与粒计算[M]. 北京: 科学出版社, 2012.

[14] 王寅杰. 云模型理论研究及其在彩色图像聚类分析中的应用[D]. 兰州: 兰州交通大学, 2013.

Study of Unconventional Reliability Measure Methods in the Case of Several Uncertainties Coexisting

Li Lingling Duan Chaoying Li Zhigang

（Province-Ministry Joint Key Laboratory of Electromagnetic Field and Electrical Apparatus Reliability Hebei University of Technology Tianjin 300130 China）

A variety of uncertainties including randomness, fuzziness and incomplete credibility coexist in reality. Even though this situation is common, it is not fully researched. An unconventional method is proposed which can deal with above-mentioned uncertainties. This method is based on fuzzy theory and cloud theory. First, make the incomplete credibility information of fuzzy stress and intensity variables cloudization by using the theory of cloud. And get the Gaussian cloud formed interval-valued Fuzzy sets which are described by the upper and lower membership functions at different credibility. Then, deal with upper and lower membership functions to make them have the mathematical characteristics of probability density function. In this way, the upper and lower limit values can be calculated with conventional stress-intensity interference model and a reliability interval can be constructed. At last, the reliability measure results curve which consists of a series of reliability intervals and their corresponding credibility can be obtained. The method not only can deal with a variety of uncertainties comprehensively, but also can keep more information in reliability measure results.

Reliability measure, randomness, fuzziness, incomplete credibility, int erval-valued Fuzzy sets, Gaussian cloud

TB114.3

李玲玲 女，1968年生，教授，博士生导师，研究方向为电器可靠性、电力系统及其自动化。

国家自然科学基金（51377044, 51475136），河北省自然科学基金（E2014202230）和河北省高等学校创新团队领军人才培育计划（LJRC003）资助项目。

2014-07-30 改稿日期 2014-09-19

段超颖 女，1990年生，硕士研究生，研究方向为电器可靠性检测技术。