“用教材”重组内容,“重预设”发展能力
——以一节“分式复习课”为例
2015-04-06江苏省扬州市江都区大桥镇嘶马中学王甫
☉江苏省扬州市江都区大桥镇嘶马中学 王甫
“用教材”重组内容,“重预设”发展能力
——以一节“分式复习课”为例
☉江苏省扬州市江都区大桥镇嘶马中学 王甫
复习课所教内容是一首老歌,如何“老歌新唱”一直是研讨的重点和难点.最近笔者有机会开设一节分式复习研讨课,选择了两个问题数学情境,不仅有效地复习了分式的运算、变形能力,而且又训练了学生可持续发展的能力,得到听课同行的好评.本文整理该课教学设计,与大家分享,欢迎批判指正.
一、“分式复习课”教学设计
1.开课阶段
预设意图:用一组简单的识别分式问题引入新课,这些简单的分式都是后续问题中会出现的.
2.容器中的水能倒完吗
问题2:一个容器中装有1L水,按照如下要求把水倒出:第1次倒第3次倒出的水量是第2次倒出的水量是第4次倒出的水量是按照这种倒水的方法,这1L水经过多少次可以倒完?
启发问题:(1)第2次倒出的水量是____L;第3次倒出的水量是____L.
(2)倒3次一共倒出的总水量为多少升?列出算式表示.
(3)倒n次水倒出的总水量为多少升?列出算式表示.
预设点评:这道问题获得解答之后可以引导学生思辨两个话题,第一,严格按照这样的规则倒水能否做到?第二,如果能够做到,通过有限次实验是否能断定以后能将水全部倒出?也就是说,让学生明白,完全依靠实验来验证预测的结论是有困难的.因此,依靠数学方法分析这个问题的优越性就更能显现出来,这也是阅读与思考的教育价值所在.
3.探究比例的性质

成果扩大:还可以进一步变形,得出哪些等式呢?
性质应用:如图1,四边形ABCD中,点E、F分别在边AB、CD上,连接EF.已知

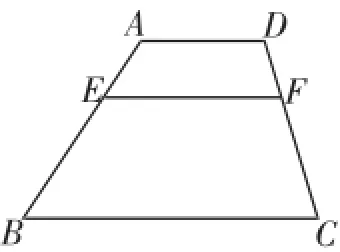
图1
4.反馈检测

命题意图:第(1)、(5)题主要对应比例式的反馈检测;第(2)、(3)、(4)题对应“容器中的水能倒完吗”的教学内容.
二、进一步的思考
教材是编写组专家团队以国家课程标准为依据精心打磨而成,其中每个栏目的设计、素材的呈现都有教学意图和设计导向,对此一线教师应该认真研读并深刻理解,创造性地开发课例,发挥教材功能,提高教学效益.以下再围绕重视复习课如何“用教材”、重组教材内容这个话题提出一些初步的思考.
1.教材没有直接安排复习课,需要教师构思教学内容
众所周知,现行各种版面的初中数学教材都没有复习课的安排,只是一个章末小结(知识内容的框图或几段小结文字),然后是章末复习题.然而每章教学结束之后,复习课总是必备的,很多复习课只是简单选择各级考题作为例习题训练,而缺少必要的主题或主线聚焦,这里教师就需要精心构思教学内容,将复习课定位在复习哪个主题,然后围绕这个主题选编教学内容.像上文中我们选择了两个情境问题,一是容器中的水能倒完吗;一是比例式的探究.这两个数学情境不仅对于复习分式的相关内容有较好的价值,同时又是学生未来学习的基础,值得玩味.
2.在“用教材”的视角上,需要教师重组教材内容
钟启泉教授曾指出:“唯有‘用教材教’才能反映教学过程中教材的性质.这是因为教学过程是一种社会交互作用的过程.知识不是教师通过传递信息强制性地灌输给学生的,而是学生自身,以及在与教师的交互作用之中建构的.”作为复习课的内容选择与重组来看,恰恰需要教师发挥专业能力,重组教材内容,重视教材上的探究、阅读理解、例题习题的拓展性与生长性,从而开发出系列追问,我们在上文中针对比例式的系列设问,不仅证明了更比式、反比式、合比式、合分比式,又在此过程中传递给学生如何研究数学的基本套路,即可以从特例引路获得相对准确的猜想方法,进一步推理论证,获得性质与应用性质.
3.本着“可持续发展”追求,需要教师熟悉学段内容
研习《义务教育数学课程标准(2011年版)》会发现,一共分为三个学段,有些内容在三个学段中都会出现,有些内容则会在第二、三学段重复出现,然而课程标准对这些内容的教学要求是不一样的,这些差别应该是一线教师做到心中有数的,唯有这样,才能准确辨别各学
段特征,在教学内容的选取、教学目标的制定上不超标、不越位.然而,就本学段而言,教师也不能只盯住所教授的这一章、这一单元的内容而不顾前后,比如,在比例式的探究中,我们把问题拓展到四边形、三角形中,比例式就是一种本着学生可持续发展的追求,因为学生在后续的几何学习中将会涉及相似三角形,而相似三角形的学习需要有扎实的比例式的基础.根据我们的教学经验,学生在接触平行线分线段成比例、相似三角形所带来的比例关系时,总有三分之一左右的学生对于比例式的适应性偏弱,不少备课组因此还会增加比例式的习题课来缓解这部分学生的不适应性.在这个意义上说,教师在分式教学过程中,基于对学段内三个年级内容的融会贯通,则可以发挥更好的专业引领作用,让学生在分式学习时就对比例式有较好的变形能力.
三、写在后面
人教社中数室资深编审章建跃老师在文2中指出:“教学设计能力是教师专业水平和教学能力的关键,其本质是‘理解数学,理解学生,理解教学’的水平和能力.”本文中我们给出的课例正是基于“三个理解”后的尝试与开发,课例的形式和内容还比较个性化,也很初步.“孤举者难起,众行者易趋.”期待更多的实践跟进,让复习课例研究丰富起来,深入下去.
1. 钟启泉.新旧教学的分水岭[J].基础教育课程(上),2014(2).
2. 章建跃.全面深化数学课改的几个关键[J].课程·教材·教法,2015(5).
3. 张奠宙.“道德经”与数学归纳法[J].数学教学,2014(9).
4. 张奠宙.《课程标准》是家,不是牢房[J].数学教学,2014(3)
