基于APOS理论的“代数式复习”教学设计探索

☉江苏省江阴市敔山湾实验学校 金岳

基于APOS理论的“代数式复习”教学设计探索

☉江苏省江阴市敔山湾实验学校 金岳

美国教育家杜宾斯基在上世纪80年代提出了一种关于数学概念教学的理论模型.他认为数学概念的建立应该包含以下四个阶段：活动（Action）、程序（Process）、对象（Object）、图示（Scheme），取四个阶段的英文首字母，命名为APOS理论.APOS理论认为，学生学习数学概念的过程是一种自我心理的建构过程.因此，在数学概念的教学中，教师应努力引导学生经过思维的操作、过程和对象等多个阶段，使学生在自主建构和不断反思的基础上，把概念组成图示，不断经过同化过程，完善自己的知识结构，顺利完成对概念的理解和掌握.

鉴于APOS理论对于数学概念教学的科学性和实用性，笔者以苏科版教材“代数式复习”为载体，对如何进行数学概念的教学设计进行一次有益的探索，借此谈谈笔者对于APOS理论运用于概念复习课的一些理解.

一、教学过程

（一）活动阶段（Action）——提出问题，创设情境

教师：很好，刚才这位同学带着我们梳理了本章知识要点，下面就来回顾做习题时我们曾经出现的错误，希望大家在今后的练习中引以为戒.

投影展示学生整理的错题，教师归纳.

教师板演：单项式的系数、次数的错误.

（2）多项式-3a2b-x-y的次数是5，它是个五次三项式.

教师板演：多项式次数误加.

教师板演：单项式、多项式、整式的归类错误.

教师板演：去括号时系数漏乘.

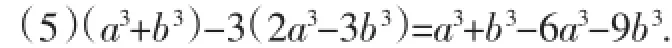
教师板演：去括号时符号误判.

教师：除了以上几个错误，老师还提醒大家：（6）合并同类项时系数的误算；（7）代数式求值时有理数运算出错.这两点也需要大家注意.

设计意图：让学生归纳整理练习中的错误，是对过去学习的回顾与反思，让学生再次梳理平时曾出现的错误，更是对今后解题的提醒，学生自我的提醒比教师直接给出的提醒，对于学生来说印象更为深刻.

教后反思：本环节中，学生对于错误一眼识别，起到了很好的警示作用.同时也教会了学生在今后的学习中也要经常对自己犯过的错误回顾反思，避免相同错误的多次发生.

（二）过程阶段（Process）——尝试探索，体验新知

（1）用代数式表示：

①比a的相反数大2的数________；②x的平方的3倍与-7的和________.

（3）单项式-π2x2y的系数是______，次数是_______.

（4）若5a4b与2a2xby是同类项，则x-y=___________.

让学生练习，教师投影后，集体批改.

设计意图：通过练习，进一步夯实基础，也是对上一个环节的检验，趁热打铁，在练习中避免上述错误的发生.

教后反思：学生解题时，教师应该指出学生练习中的错误，实时批改，加深学生印象.

（三）对象阶段（Object）——认识概念，动手操作

（1）请你按照如下的数字规律，分别写出第n个数字：（n为正整数）

①2，4，6，8，10，…，____；

②1，3，5，7，9，…，____；

③3，5，7，9，11，…，____；

④2，4，8，16，32，…，______.

（2）用火柴棒按以下方式拼搭，第n个图形需要_____根火柴棒.

把第一根火柴棒单独看，第一个图形需要（1+3）根火柴棒，第二个图形需要（1+3×2）根火柴棒，…，所以第n个图形需要（3n+1）根火柴棒.

……

把前两根火柴棒单独看，第一个图形需要（2+5）根火柴棒，第二个图形需要（2+5×2）根火柴棒，…，所以第n个图形需要（5n+2）根火柴棒.

……

把前三根火柴棒单独看，第一个图形需要（3+7）根火柴棒，第二个图形需要（3+7×2）根火柴棒，…，所以第n个图形需要（7n+3）根火柴棒.

m个m个m个m个m个m个

学生分组讨论，把前m根火柴棒单独来看，第一个图形需要（m+2m+1）根火柴棒，第二个图形需要［m+ 2（2m+1）］根火柴棒，…，所以第n个图形需要［m+（2m+ 1）n］根火柴棒.

设计意图：让学生感受到代数式是数学符号组成的语言，是刻画数量关系的重要工具.在数学中，从几个简单的例子入手，发现规律，并用代数式来表示规律，体现了数学中的归纳思想，让学生了解数学思想方法.

教后反思：第（2）题中用代数式来表示规律，不仅可以从图形中发现规律，根据数形结合的思想，其实从前三小题中，也可以根据数的规律来得到第（2）题第④小问的规律，更为简便.在数学归纳思想中，规律的推出还需要证明，还应指导学生将第一个图形的答案代入式子，以检验用于表示规律的代数式是否正确.

（四）图示阶段（Scheme）——作图比较，共同提高

学生到对照屏幕，进行讲解，复习本章基本概念.

设计意图：让学生自行梳理知识结构，让学生自主参与复习，培养学生复习的习惯，提高学生学习的积极性，让学生的说代替教师的讲，更好地体现课堂上以学生为主体的教学理念.

教后反思：在本环节中学生积极参与，在优秀作业的展示中激发了学生学习的兴趣，也教会了学生知识梳理的方法，对于以后学生其他知识的复习也起到了很好的示范作用.

二、课后反思

APOS理论认为，对于代数式概念的理解是一个循序渐进、螺旋上升、逐步深入的长期过程，因此教师对代数式概念的教学过程也必定是长期的，在这个漫长的过程中，笔者认为应该注意以下几点.

1.关注概念形成和概念内涵之间的关系，选择恰当的教学策略

几何直观是一种重要的科学的研究方式，它是认识科学知识的基础，有助于学生对数学知识的理解.同时它又是一种创造性思维，是揭示现代数学本质特性的一个重要工具.教师在教学过程中，设法针对学生的认知特点，充分利用图形帮助学生去认识和感受代数式的图形应用，帮助学生建立用图形观念去解决问题的意识，让学生借助图形感受代数式在研究数学问题和生活实际问题中的作用，从而加深对代数式概念本质的认识和理解，同时也体现了几何直观、数形结合等重要数学思想方法在数学学习中的意义和作用.在代数式教学中，学习代数式的形式化表述是一个基本要求，我们更主要的是让学生理解为何要形式化、为何要这样形式化，突出对数学本质的认识，否则生动活泼的数学思维活动将淹没在形式化的海洋里.所以在教学中，应当把直观和形式进行有机结合，通过对生活现象中的典型案例进行直观分析和自主探索，让学生体验代数式概念逐步形成的过程，感受蕴含其中的数学思想方法，跟随代数式概念发展的足迹，将数学知识从抽象的学术形态转化为学生易于接受的教育形态.在创设问题情境时要注意：问题情境要适合学生的生活体验，并且能够揭示代数式概念的现实背景、形成过程.

2.重视与其他知识的联系，培养学生的数学思维能力

本课是《代数式》一章的复习课，对于基本概念、基本知识、基本技能的掌握，在复习课上不应该是简单的重复，所以采取了学生自主复习的形式，让学生自己梳理知识脉络，自己归纳整理错题，让所有学生参与到复习中来，也指导了学生复习的方法，希望学生学会复习.温故而知新，希望学生通过本课能有所提升，让学生更深刻地理解本章内容，所以对本章涉及的数学思想进行了整理复习.代数式作为方程及函数学习的基础，对于后续的学习有着非常重要的作用，因此这一点也应在本课上让学生有所体会.在课堂上，还有许多细节之处没有很好地处理，也需要在今后的教学中不断改进提高.

所以在教学过程中，教师应该关注学生代数式概念的认知发展情况，不断调整教学策略，引导学生运用观察、分析、抽象、综合等数学思维方法主动获取知识，在总结归纳中帮助学生理清知识结构，为进行更高层次的思维活动打好基础.同时合理设计问题，促使学生进行积极地反思，“为何这么做”“如何得到”等，在总结和反思中形成数学思想方法.这对学生的代数式概念认知从“活动”到“过程”再到“对象”，最后建立“图式”这样分层次的建构过程有着重要意义.

1.张维忠.文化视野中的数学与数学教育［M］.北京：人民教育出版社，2005.

2.朱宸材，浦叙德.慧眼识图巧手指路思维提炼［J］.中学数学教学参考（中），2013（9）.

3.于新华，杨之.数学理解的层次性及其教学意义［J］.数学通报，2005（2）.Z