中新两国初中数学教材的对比研究——以人教版、北师大版、新加坡教材中“勾股定理”为例

☉西北师范大学教育学院☉甘肃省酒泉第四中学 徐玉庆

中新两国初中数学教材的对比研究
——以人教版、北师大版、新加坡教材中“勾股定理”为例

☉西北师范大学教育学院☉甘肃省酒泉第四中学 徐玉庆

“勾股定理”是平面几何中有关度量的最基本定理，它从边的角度进一步刻画了直角三角形的特征.学习勾股定理及其逆定理是进一步认识和理解直角三角形的需要，也是后续有关几何度量和代数学习的必要知识，同时也是初高中知识衔接的重要知识.勾股定理的内容涉及图形、二次根式、几何证明.义务教育的课程标准从1963年的《全日制中学数学教学大纲》［1］、2000年的《全日制义务教育初中数学教学大纲（使用修订版）》［2］、2001年的《全日制义务教学数学课程标准（实验稿）》［3］，到2011年的《义务教育数学课程标准》［4］，历经半个世纪，课程标准中对义务教育阶段的知识进行不断地完善和改进，由于不同的编者对于课程标准理解的不同，因此，我们根据2011年的《义务教育数学课程标准》选择了目前在全国使用范围较广、版本最新的2013年9月出版的人教版［5］和2013年12月出版的北师大版教材［6］.新加坡初中学生在历年的TIMSS测试中名列前茅，同时在KASSEL中学数学国际比较中，新加坡学生的测试成绩也遥遥领先，因此，我们选择2007年出版的New Mathematics Counts for Secondary 2 Normal（Academic）Singapore［7］.对以上三个版本教材中“勾股定理”的习题进行认知水平的分析和难度模型的分析.

一、教材样本及习题数量

表1：教材样本及习题总数

本文中的习题包含人教版教材“勾股定理”中的“例题”“练习”“复习巩固”“综合运用”“拓广探索”“数学活动”；北师大版教材“勾股定理”中的“例题”“随堂练习”“知识技能”“问题解决”“数学理解”“联系拓广”；新加坡教材“勾股定理”中的“例题（Example）”“练习（Exercise12a、12b）””Review Question”“Problem Solving”“Revision Exercise”.

从习题的总量来看，新加坡教材习题所占最高，达到36%，其次是人教版教材习题所占35.5%，北师大版版教材习题数量所占仅为28.5%，远低于新加坡教材和人教版教材习题的数量.

二、习题认知水平的比较

布鲁姆在《教育目标分类学》中把认知目标分为知道（知识）（knowledge）、领会（comprehension）、应用（application）、分析（analysis）、综合（synthesis）、评价（evaluation）六种水平.经顾泠沅教授改进，分为四个层次框架.水平1：计算——操作性记忆水平；水平2：概念——概念性记忆水平；水平3：领会——说明性理解水平；水平4：分析——探究性理解水平.根据以上数学认知水平分析框架，本文将三个版本的习题进行分类统计，计算出三个版本教材中习题在各个水平所占的比例.

表2：三个版本教科书习题数学认知水平

如表2所示，在水平1方面，新加坡教材所占比例最大，远高于人教版教材和北师大版教材，人教版教材和北师大版教材在水平1方面相差不大；在水平2方面，人教版教材占18%，而北师大版教材只占3%，新加坡教材在概念性记忆水平上为0.0%；在水平3方面，新加坡教材占了52%，要远远高于人教版教材和北师大版教材的水平；在水平4方面，人教版教材高于北师大版教材和新加坡教材的水平.

从整体上看，人教版教材的水平最高，高出北师大版0.41，高出新加坡教材0.9.新加坡教材的习题水平相对较低.

三、三个版本教材习题的难度比较

1.数学综合难度模型

2009年，鲍建生教授在《中英初中数学课程综合难度的比较研究》［8］中提出综合难度模型，对中英期望课程综合难度做了比较，给教材的国际比较提供了一个平台.其中难度因素包含探究、背景、运算、推理和知识含量五个因素，每一个难度因素又划分为不同的水平，具体如表3.

表3：难度因素及水平划分难度因素

2.习题难度模型的比较

对三个版本的教材统计结果如表4所示.

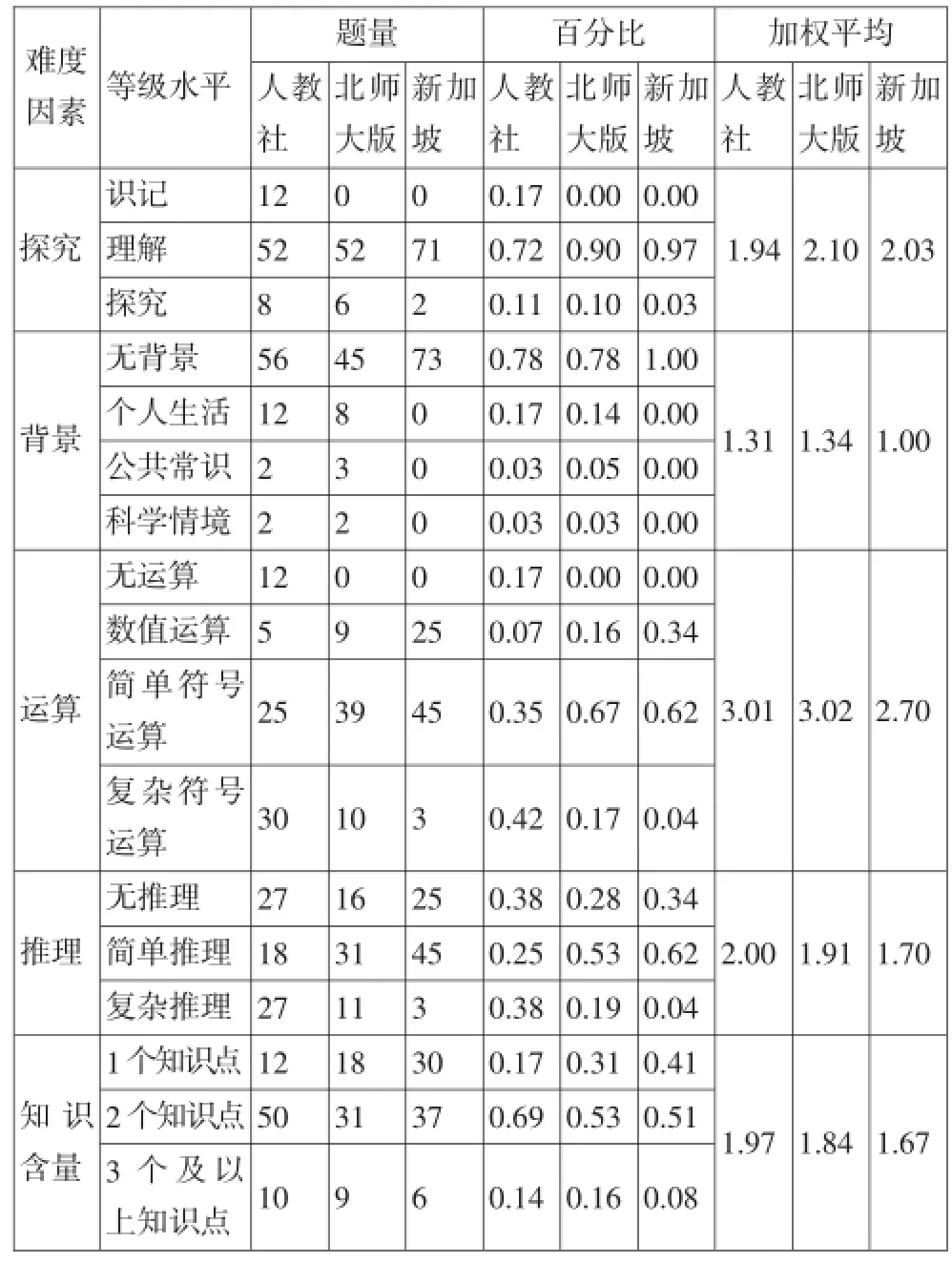
表4：三种教材“勾股定理”习题的综合难度比较

（1）探究因素的难度分析.

统计表明，人教版、北师大版、新加坡教材中“识记”水平的习题分别占17%、0%；属于“理解”水平的习题分别占72%、90%、97%；属于“探究”水平的习题分别占11%、10%、3%.人教版教材在“识记”水平方面要远远高于其他两个版本的教材，在“探究”水平方面也高于其他两个版本，但在“理解”水平方面要低于其他两个版本.

（2）背景因素的难度分析.

统计发现，新加坡教材所有习题都没有涉及实际背景，人教版和北师大版教材中“无背景”的习题均占78%；“个人生活”的习题分别占17%、14%；“公共常识”的习题分别占3%、5%；属于“科学背景”的习题均占3%.

从统计结果发现，人教版和北师大版的习题在实际背景方面还是很富有变化的，许多题目和学生的实际生活紧密联系.相比之下，新加坡教材的习题在题目的背景上非常欠缺，73道题目中没有一道题目涉及实际背景.

3.运算因素的难度分析.

从表4的统计结果发现，人教版“无运算”的习题占17%，其他两个版本都没有“无运算”的题目；人教版、北师大版、新加坡教材中属于“数值运算”的分别占7%、16%、34%；属于“简单符号运算”的分别占35%、67%、62%；属于“复杂符号运算”的分别占42%、17%、4%.

人教版“无运算”题目所占比例最大，新加坡教材“数值运算”的题目所占比例最大，北师大版“属于简单符号运算”的题目所占比例最大，属于“复杂符号运算”的题目人教版教材远远高于其他两个版本.

（4）推理因素的难度分析.

人教版、北师大版、新加坡教材中“无推理”的题目分别占38%、28%、34%；“简单推理”的题目分别占25%、53%、62%；属于“复杂推理”的题目分别占38%、19%、4%.

人教版教材中“无推理”的题目所占比例最大.新加坡教材中“简单推理”的题目所占比例最大，在“复杂推理”的题目中人教版教材所占比例最大.

（5）知识含量因素的难度分析.

统计结果表明，人教版、北师大版、新加坡教材中含有“1个知识点”分别占17%、31%、41%；含有“2个知识点”的题目分别占69%、53%、51%；含有“3个及3个以上知识点”的题目分别占14%、16%、8%.

新加坡教材中含有“1个知识点”的题目所占比例最大，含有“2个知识点”的题目中人教版教材所占比例最大，北师大版教材含有“3个及3个以上知识点”的题目所占比例最大，新加坡教材中含有“3个及3个以上知识点”的题目涉及较少.

（6）比较结果.

根据前面三种不同版本的教材习题难度，得到各水平的等级量度的加权平均，如表5所示.

表5：三种教材“勾股定理”习题难度的加权

四、研究结论

结合习题的认知水平和习题的综合难度比较，人教版的习题难度是最大的，然而人教版“识记”水平相对较高，其主要原因是教材编写的设计，人教版在勾股定理和勾股定理的逆定理之后自然地引出原命题和逆命题的知识点，所以在“识记”水平方面的题目相对较多.新加坡教材的习题数量较多，但是没有一道题目涉及实际背景，更加注重题目的运算.人教版和北师大版教材在习题设计中都有“联系拓广”，导致在“运算”“推理”方面难度较大.北师大版在题目的设计上关注题目的实际背景，这样更贴近学生的实际生活.

最后，本文从习题的认知水平和综合难度模型两个方面做了比较，对于教材习题难度的比较提供了一种新的思路，对于教材难度的分析有了更深入的研究，对于教材的编写者和教材的选择者具有一定的价值.

1.中华人民共和国教育部制订.全日制中学数学教学大纲（草案）［M］.北京：人民教育出版社，1963.

2.中华人民共和国教育部制订.全日制九年义务教育初中数学教学大纲［M］.北京：人民教育出版社，2001.

3.中华人民共和国教育部制订.全日制义务教育数学课程标准（实验稿）［M］.北京：人民教育出版社，2001.

4.中华人民共和国教育部制定.义务教育数学课程标准（2011年版）［M］.北京：北京师范大学出版社，2012.

5.课程教材研究所中学数学课程教材研究开发中心.义务教育课程标准试验教科书·数学·八年级（下册）［M］.北京：人民教育出版社，2013.

6.课程教材研究所中学数学课程教材研究开发中心.义务教育课程标准试验教科书·数学·八年级（上册）［M］.北京：北京师范大学出版社，2013.

7.New Mathematics Counts for Secondary 2 Normal（Academic）［M］.Singapore：Marshall Cavendishi Education，2007.

8.鲍建生.中英初中数学课程综合难度的比较研究［M］.南宁：广西教育出版社，2009.

9.史宁中，孔凡哲，李淑文.课程难度模型：我国义务教育几何课程难度的对比［J］.东北师大学报（哲学社会科学版），2005（6）.

10.孔凡哲，史宁中.四边形课程难度的定理分析比较［J］.数学教育学报，2006，15（1）.

11.张维忠，黄丽虹.新教材“三角形”课程难度的对比分析［J］.数学教育学报，2009，18（4）.

12.王建磐，鲍建生.高中数学教材中例题的综合难度的国际比较［J］.全球教育展望，2014，43（8）.

13.贾随军，吕世虎，李保臻.中国与美国初中数学教材习题的个案比较——以“与三角形有关的角”为例［J］.数学通报，2014，53（9）.Z