一类代数问题的三角解法
2015-04-05查正开常熟市中学江苏常熟215500
●查正开(常熟市中学江苏常熟215500)
一类代数问题的三角解法
●查正开(常熟市中学江苏常熟215500)
文献[1]通过对一些数学奥林匹克不等式试题的分析,发现一些不等式的共同背景,即在“p,q,r为正实数,且p2+q2+r2+2pqr=1”的条件下证明某个不等式,得出了该条件下的5条性质,并应用这些结论来证明有关条件不等式.
性质设p,q,r为正实数,且p2+q2+r2+2pqr=1,则
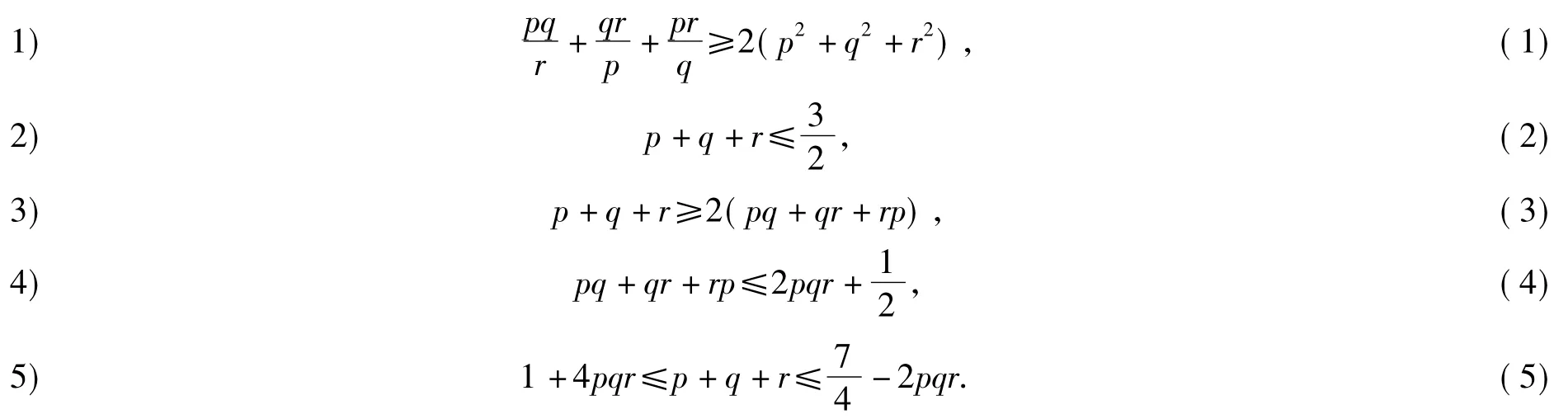
由于这些性质形式差异较大,其证明方法也各不相同,加之证明技巧性很强,因此难以让学生理解和掌握.笔者受文献[2]的启发,通过思考探究出这类条件问题的几何本质,并由此得出这些性质的统一三角法证明,从而可“模式识别”,轻松自然地得到这类问题的一般解法.
一方面,在△ABC中,
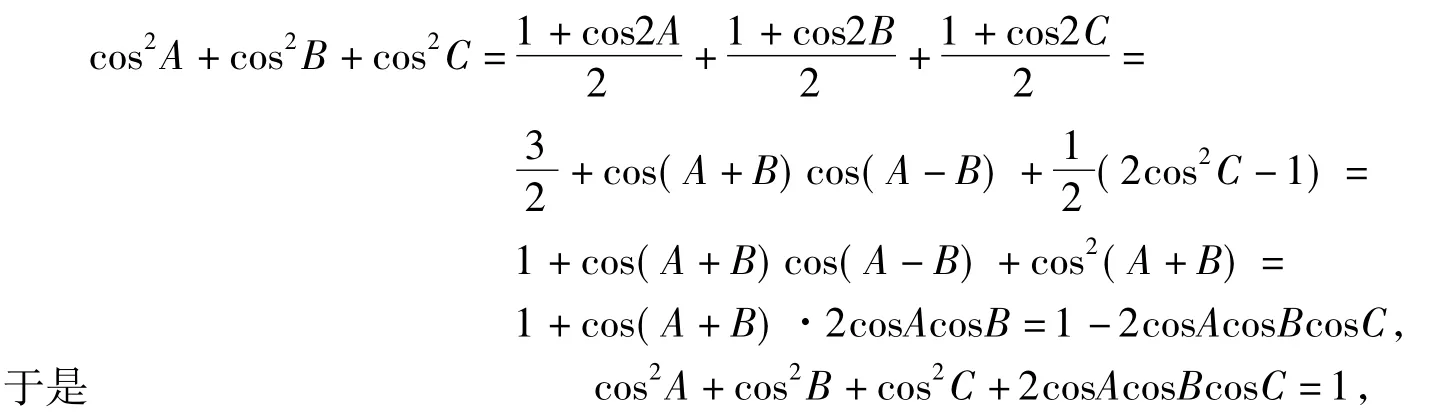
这说明cosA,cosB,cosC满足其条件中的等式.
另一方面,若设p=cosA,q=cosB,r=cosC,因p,q,r是正实数,故不妨设,则条件等式变为cos2A+cos2B+cos2C+2cosAcosBcosC=1,即

因为A,π-B-C∈(0,π),得A+B+C=π,所以A,B,C可作为某锐角三角形的3个内角.
综合上述2个方面可得如下定理:
定理正实数p,q,r若满足p2+q2+r2+2pqr=1,则它们分别对应于某锐角三角形的3个角的余弦.
由本定理我们得出“p,q,r为正实数,且p2+q2+r2+2pqr=1”的代数条件即为三角形问题的几何本质,从而文献[1]的性质可给出统一的三角证明:
由条件根据上述定理可设p=cosA,q=cosB,r=cosC,则性质1)所证不等式(1)即:在△ABC中,
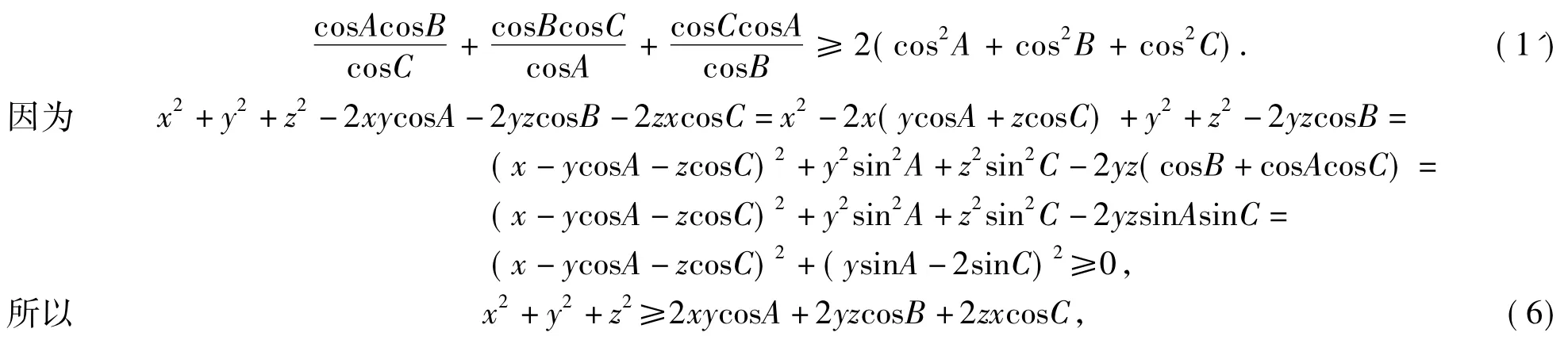
在不等式(6)中令xy=cosA,yz=cosB,zx=cosC,立得式(1')成立.
性质2)即证明:在△ABC中,

因为在△ABC中,
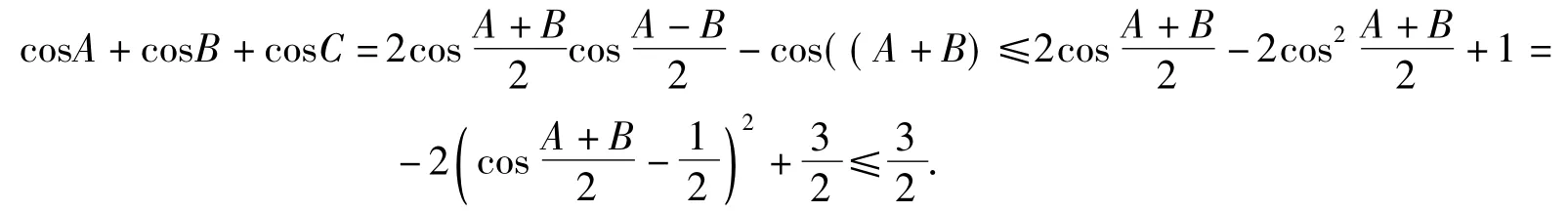
性质3)即证明:在△ABC中,
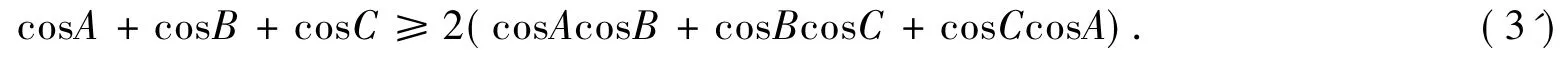
利用熟知的不等式可得

性质4)即证明:在△ABC中,

根据抽屉原理知,在△ABC的3个角中必有2个角同时不大于或不小于,不妨设为A,B,则
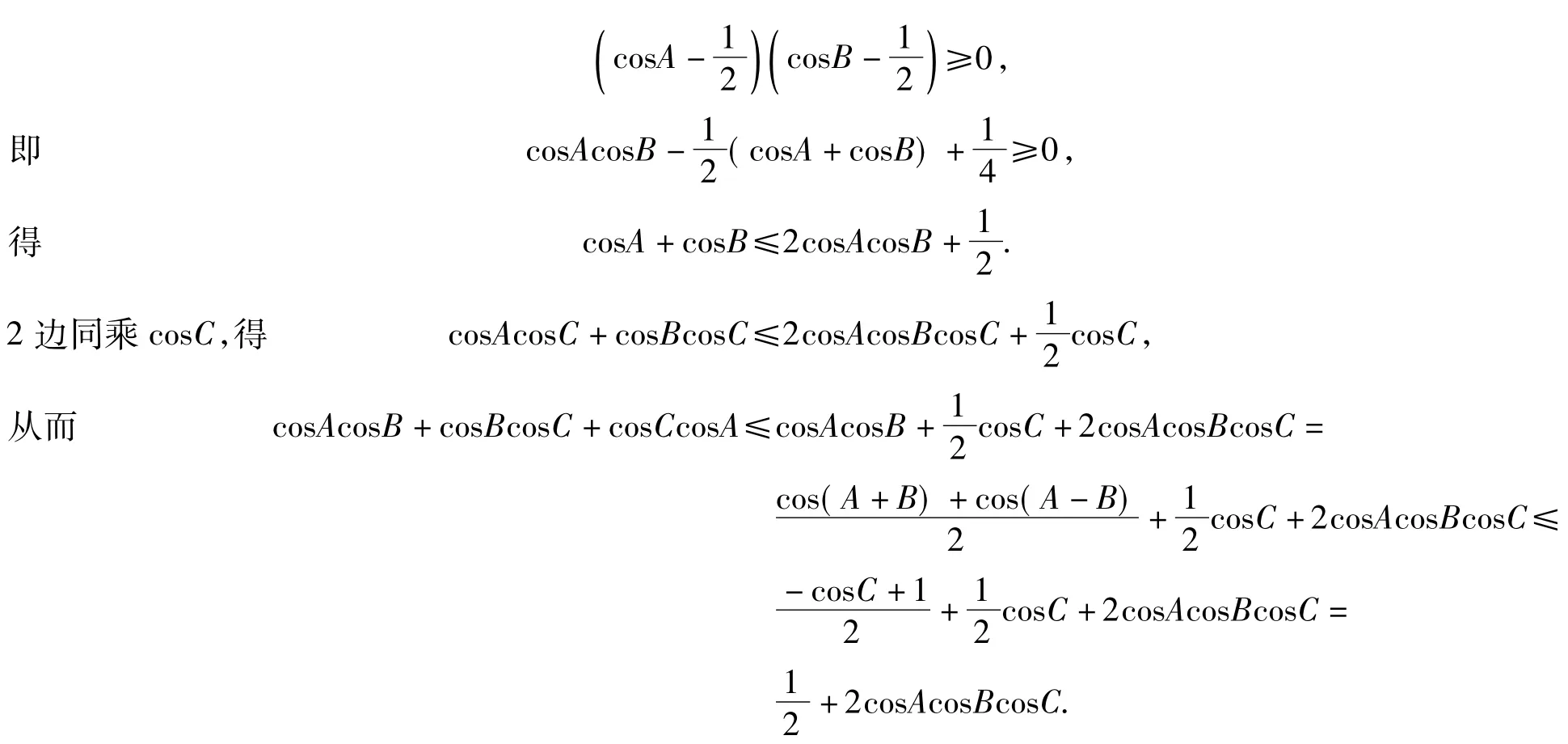
性质5)即证明:在△ABC中,
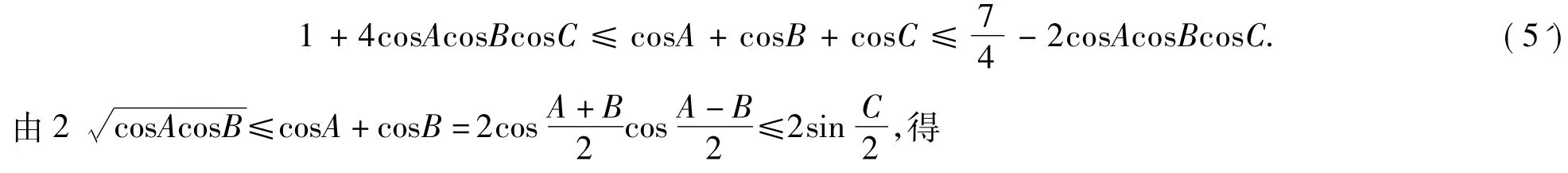
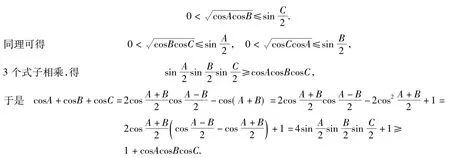
故不等式(5')左边成立.又因为
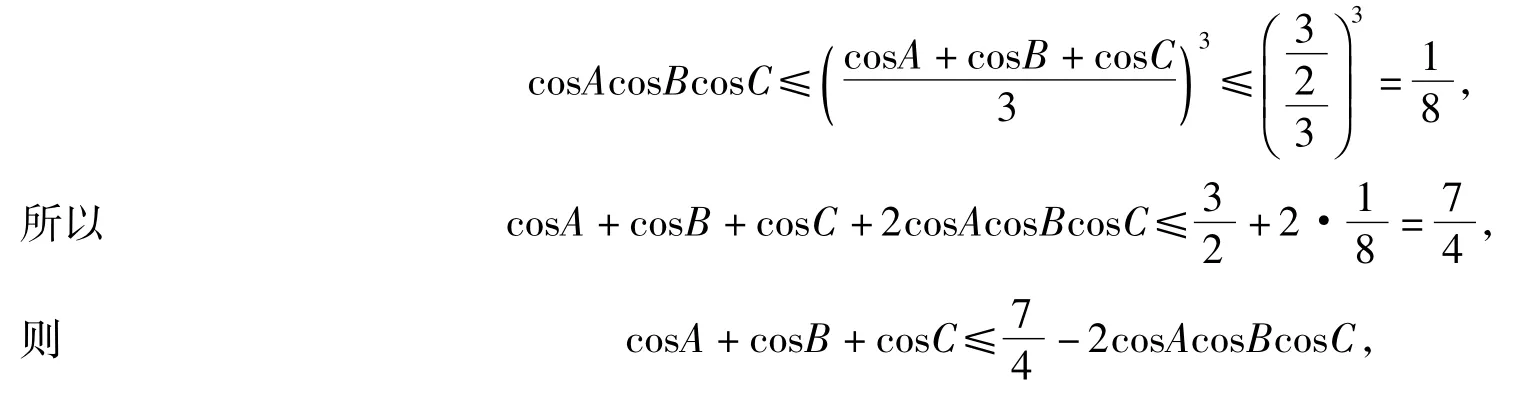
故不等式(5')右边也成立.
由上述证明可知,文献[1]中所给出的“p,q,r为正实数,且p2+q2+r2+2pqr=1”条件下5个性质应用定理进行转化,运用三角知识均可得到简捷高效的证明.因此我们无需刻意来记住这些结论,若碰到这类条件下的问题直接抓住其几何本质,利用“三角”这把利器可迅速求解.
例1已知x>0,y>0,z>0且x2+y2+z2+2xyz=1,求证:
(《学数学》2015年第1期数学贴吧问题)
分析根据题设条件可直接利用定理,将问题转化为一个简单的三角不等式.
证明设x=cosA,y=cosB,z=cosC,则由上述定理结论知A,B,C为锐角△ABC的3个内角,则
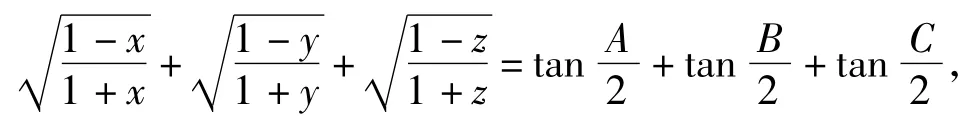
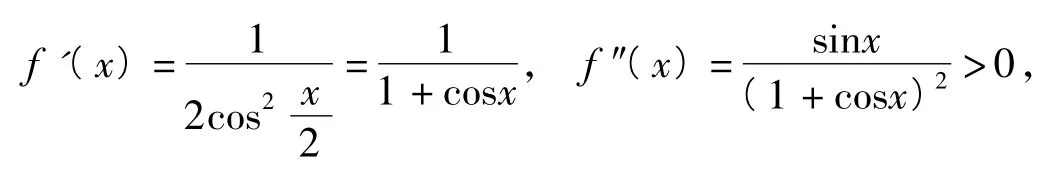
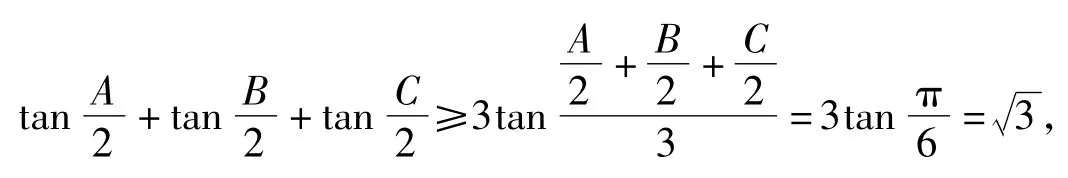
因此,原不等式成立.
例2设a≥1,b≥1,c≥1,且满足abc+2a2+2b2+2c2+ca-cb-4a+4b-c=28,求a+b+c的最大值.
(2011年全国高中数学联赛加试试题)
分析由已知变形得,令a-1=4p,b+1=4q,c=4r,则已知等式即为p2+q2+r2+2pqr=1.
解设p=cosA,q=cosB,r=cosC,则由定理知A,B,C为锐角△ABC的3个内角,利用熟知的不等式,得

说明对于不等式,除了性质2证明中的方法外,还可构造函数,由f(x)为凸函数,利用琴生不等式得到证明.
例3设正实数u,v,w满足,求证
(第48届中国国家集训队测试题)
分析由u,v,w为正实数可令u=4p2,v=4q2,w=4r2,其中p>0,q>0,r>0,则条件等式即为p2+q2+ r2+2pqr=1.
证明设p=cosA,q=cosB,r=cosC,则由定理知A,B,C为锐角△ABC的3个内角,所证不等式即为
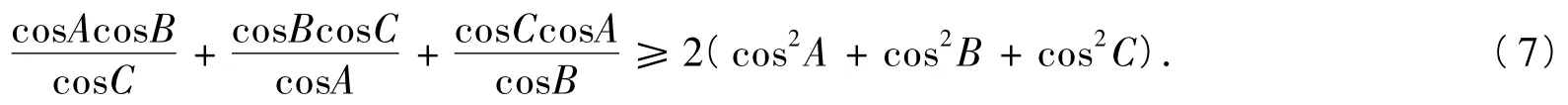
由于△ABC中有嵌入不等式(6),令xy=cosA,yz=cosB,zx=cosC,代入(6),立得式(7)成立.
例4设非负实数x,y,z满足x2+y2+z2+xyz=4,证明:xy+yz+zx-xyz≤2.
(第30届美国数学奥林匹克竞赛试题)
分析当3个数中有1个或2个数取0时命题显然成立,故只需考虑正实数x,y,z的情形.
令x=2a,y=2b,z=2c,则命题转化为“正实数满足a2+b2+c2+2abc=1,求证:
证明由定理可设a=cosA,b=cosB,c=cosC,则命题即为:已知△ABC,求证:

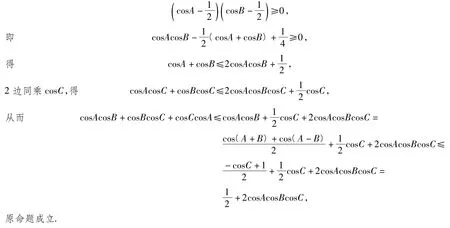
由此可知,应用定理可将“p,q,r为正实数,且p2+q2+r2+2pqr=1”条件下的一类代数问题转化为三角问题,借助三角知识可以简捷处理.需要指出的是:这类条件问题的竞赛试题经过命题者精心包装和整合改编,其形式变幻莫测,外表众彩纷呈.解题者应通过变形转换,拨开它们的神秘面纱和虚假外壳,揭示并暴露其几何本质,模式识别地运用三角知识,给出简捷优美的解答.
最后笔者再提供几个经典试题,读者可采用上述方法自行加以解答,相信对这类问题会有更深入的理解和体会.
练习测试题:
(2007年美国国家集训队试题,2007年伊朗数学奥林匹克竞赛试题)
提示:将条件变形为x2y2+y2z2+z2x2+2x2y2z2=1,令xy=p,yz=q,zx=r,则问题转化为“正实数p,q,r满足p2+q2+r2+2pqr=1,求证:”.
2.设正实数x,y,z满足xy+yz+zx+xyz=4,求证:x+y+z≥xy+yz+zx.
(1996年越南数学奥林匹克竞赛试题)
提示:令xy=4p2,yz=4q2,zx=4r2,则已知条件即为p2+q2+r2+2pqr=1,待证式即为
(2011年中欧数学奥林匹克竞赛试题)
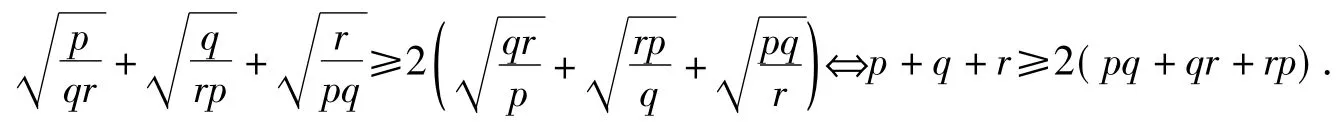
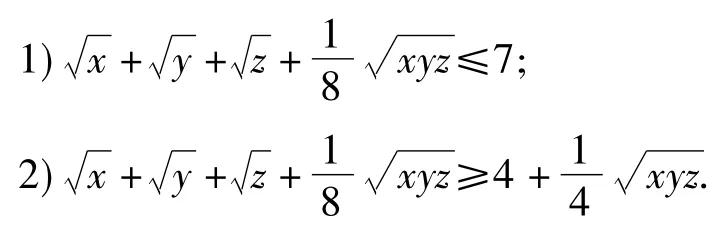
(2004年全国高中数学联赛河南省预选赛试题)
提示:作变换x=16p2,y=16q2,z=16r2(其中p>0,q>0,r>0),则问题转化为“已知正实数满足p2+ q2+r2+2pqr=1,求证:
5.已知a,b,c为正实数,a2+b2+c2+abc=4,求证:a+b+c≤3.
(第20届伊朗数学奥林匹克竞赛试题)
提示:设x=2p,y=2q,z=2r,则问题转化为“正实数满足p2+q2+r2+2pqr=1,求证:
[1]邹守文.一类不等式奥林匹克试题的共同背景[J].中学教研(数学),2012(9):43-46.
[2]程汉波.三角代换,巧证代数不等式[J].中学数学研究,2014(3):38-39.
