数学课堂学生讲题教学模式的实践探索与思考*
2015-04-05陈芳华泰顺县实验中学浙江泰顺325500
●陈芳华(泰顺县实验中学浙江泰顺325500)
●章勤琼(温州大学数学与信息科学学院浙江温州325035)
数学课堂学生讲题教学模式的实践探索与思考*
●陈芳华(泰顺县实验中学浙江泰顺325500)
●章勤琼(温州大学数学与信息科学学院浙江温州325035)
1 学生讲题:学生学习主体地位的凸显
《义务教育阶段数学课程标准(2011年版)》强调要突出学生在学习中的主体地位[1],学习由3种对话实践——同客观世界的对话、同伙伴的对话、同自己的对话构成,在这样三位一体的学习中,学生可以创设活动进行合作反思性实践来实现知识的内化[2].学生学习的主体地位归根结底是要体现在日常的课堂教学中,因而,针对学习的本质,可以让学生在课堂上进行“讲题”,通过教师和其他同伴的倾听,再经过不同学生提出问题进行串联,探讨课堂的教学活动,让全班学生参与其中,让每个学生都能通过讲题进行合作探究与深入学习.
学生讲题,其教学的实质在于以学生的学习为核心,更加突出学生的主体地位,让绝大多数学生受到良好的数学教育.在这个过程中,教师主要起点拨的作用,及时发现所讲题目的不同解法或变式,这些不同解法或变式不仅为学生提供了交流的题材,更为学生指明了思考的方向,在这里绝大多数学生是学习的研究者、发现者.强烈的问题解决意识促使生生间与师生间互动讲题,展示解题过程,深究问题解决的本质方法,完善学生的认知结构,从而较好地提升学生的思维水平.为了让学生能在课堂上讨论,教师首先需要创设一种轻松的氛围,让学生意识到要敢于向同学传达自己的思想,要珍惜能发言的机会.经过在课堂教学中的不断尝试,笔者认为学生讲题主要有以下几种切实有效的模式.
2 学生讲题的几种模式
模式1学生“画”知识,说知识框架
对于初中学生而言,如果能弄清所学知识的前后联系,深刻理解所学知识的结构,将对他们的数学学习带来很大的帮助.因此,学生讲题的第1种有效模式就是让学生通过画知识树的形式,说出所学章节知识之间的框架.如:七年级上册第1章“有理数”结束后,笔者布置学生以自己的理解方式、小组合作的形式,探讨交流画出本组所理解的知识框架图,学生花了一个周末的时间思考后再在组里达成共识画好知识树.学生所画图形丰富多彩,有的组画成鱼,认为鱼的每个部位都对应着相应的知识点:在尾巴上写出有理数分为整数与分数,在身体的鳍上分别写出了本章节相关的知识点,如数轴、绝对值等.而且,学生还写出感想,认为只有鱼身体上各条鳍上的知识都牢固掌握了,才可以让鱼游得更快.这样“画”出知识后,再让学生学知识的结构关系时,学生容易想到自己所画的栩栩如生的图片,更有利于记忆与理解.
这是一种特殊形式的“讲题”,学生并不是要就某个具体的数学题目进行讲解,而是要从更上位的知识结构角度进行思考.在这个学习过程中能够逐渐有意识地从总体上了解知识的整体结构,建立属于自己的知识体系,逐渐形成一定的认知结构,提高学习的自主性和自主学习的能力,并提升自己的总结能力.
模式2自我提问式讲题,培养学生的发散思维
在数学习题的讲解中,笔者尝试以一道题目为背景,然后层层深入进行变式拓展.在这个过程中,通过学生的自我提问,让不同程度的学生都能找到讲题的素材,都能找到成功的愉悦,并在同伴与教师的引领下,通过讲题等交流活动较大幅度地提升思维品质.譬如,笔者从这样一道简单的题目出发:如图1,关于Rt△ABC,∠ACB=90°,CO⊥AB,你知道哪些知识点?可以看出,这是一道简单的“图形与几何”中有关直角三角形的题目,通过这样开放的提问,学生可以说出的知识点有互余、勾股定理、三角形面积等.接下来,笔者对这道原题作了适当的改变,将这一三角形置于直角坐标系中,层层递进地提出了以下3个问题:
问题1在图2所示的坐标系中,CA=2,BC=5,求点A,B,C的坐标.
问题2求过点A,B,C的抛物线解析式.
问题3如图3,在问题2的抛物线中,是否存在点P使得△ABP的面积与△ABC的面积相等.
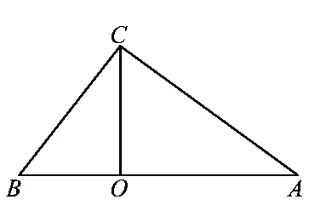
图1

图2
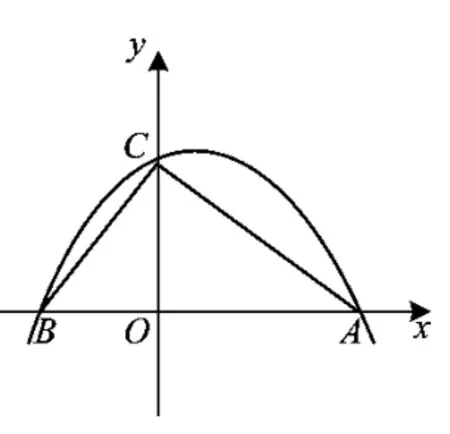
图3
在引导学生解决了这2个题目之后,教师鼓励学生以自我提问的方式提出更多的问题.经过认真的思考与激烈的讨论后,学生提出了如下一些很有价值的问题:
问题4在图3的抛物线中,在x轴的上方是否存在点Q,使△ABQ的面积为△ABC的面积的2倍.
问题5在问题3的抛物线中,在AC的上方是否存在点Q,使四边形ABCQ的面积最大.
容易看出,上述2个问题的思维含量很高,需要运用初中阶段几何与函数的很多知识综合解决,由学生自己提出,很不容易.因此,从学生熟悉的基本问题出发,用较低的问题起点使绝大多数学生都能积极成功地讲题,层层深入的、开放性的问题设置让绝大多数学生都能讲出对问题的不同理解,教师的适时点评与同伴互助让绝大多数的学生对问题的理解趋向深刻.
这种模式的讲题,重在让学生在解题过程中能时刻注意对题目进行反思,探索条件与结论可能的变式.在此基础上,鼓励学生积极提出问题,有效产生创造性思维,这种成功的讲题体验,将进一步引领学生在平时的课堂教学中自主讲题,提升思维能力,真正培养了提出问题、发现问题的能力,这便是第3种模式的讲题.
模式3以典型错例引领学生互助讲题,优化认知
心理学家贝恩布里奇说,差错人皆有之,作为教师不利用是不能原谅的,没有大量错误作为台阶就不能攀登上正确结果的宝座[3].由于初中学生认知心理还不全面,在做练习、试卷时出现错误是正常现象.教师在分析错误时,不应只告诉学生这样做是错的、怎么做是正确的,更重要的是审视错题,进行归因,提出对策,深究课堂教学行为,期望促进教学发展,这是提高课堂有效性一种重要形式.同时,应该引导学生去思考“为什么这么做”是错误的,要让学生知其然还要知其所以然.学生在思考过程中才能体会到数学学习不能只靠机械的记忆,要找到根本的原因.另外,教师放手让学生上台讲解错误的原因,这在无形中培养了学生的钻研能力.
用错误资源作为学生讲题的素材,通过部分学生的引领与生生间的积极交流,可以有针对性地纠正学生容易犯的典型错误.如浙教版九年级上册“二次函数应用2”例题3第1)小题:某饮料经营部每天的固定成本为200元,其销售的饮料每瓶进价为5元.销售单价与日均销售量的关系如表1所示:

表1 销售单价与日均销售量
1)若记销售单价比每瓶进价多x元,日均毛利润(毛利润=售价-进价-固定成本)为y元,求y关于x的函数解析式和自变量的取值范围.
基础薄弱的学生是向同学们询问例题中的日均销售量480-40(x+5-6)是何意义?基础中等的学生可以理解销售单价每增加1元则日均销售量减少40瓶,即当销售单价为x+5元时,与销售单价为6元时的情况作比较,得出日均销售量为480-40(x+5-6)=(520-40x)480-40瓶.基础中等偏上的学生根据表格的实际意义,得到销售单价为5元时,日均销售量为520瓶,因为每瓶进价为5元,可以轻松地得出销售单价为x+5元时,日均销售量为520-40x瓶.尖子生的想法是利用数学建模的思想,得到m=520-40x.
让不同层次的学生充分地思考并展开讨论,不仅使学生较好地纠正了错误的解法,而且领略到了解决函数问题时常用的画图法与计算法的不同魅力,体验了要说明一种结论不成立时,及时找反例的数学思考方法.
此外,在二次函数的教学中,为了充分提高例题教学的有效性,笔者让学生课前去找一些已知的二次函数解析式,如二次函数y=x2-3x+9怎样转换成y=a(x+m)2+k的形式等,然后与同桌交流批改,找出典型的错误解法并由学生代表上台“讲错解”,让学生在错解中加深理解用配方法求二次函数顶点坐标的通性通法,同时向同伴暴露解题障碍,及时修正自身的认知结构,提高认知基础.为了让学生体会从特殊到一般的思想方法,让数学基础相差较大的2名学生上台板演“如何把二次函数的一般式y=x2+bx+c转换成y=a(x+m)2+k,基础较好的学生成功解题后在台上及时对基础较差的学生进行现场讲题指导.因此,学生自我记录整理错题并通过适当的形式进行讲题,真正体现了学生学习的主体性,优化已有的认识,提高知识水平.在此基础上,再通过教师对学生的错题进行整理并研究学生错误的原因,反思课堂教学行为,最终促进每个学生的成长.像这样有效利用错误资源,深究问题解决本质方法的学生讲题,势必有效激发学生更加主动地探究,更加主动地讲题,从而较好地优化数学思维品质.
综上所述,通过上面3种模式,让不同层次的学生在数学课堂上积极参与讲题活动,暴露问题并及时受到师生的积极帮助,从而很好地修正自身的认知结构,优化认知基础.而对于听题的学生而言,由于讲题的是自己的同伴而非教师,因此在听的过程中会更加积极地思考,尝试发现讲题学生的错误.因此,在讲题交流中,不仅较好地突破了学生的认知障碍,而且丰富了学生的解题经验.教师的适时点拨与讲评,让不同的认知及时转化,促使学生的认知水平不断提升,从而让学生看到不变的数学本质.同时学生的讲题,让学生及时得到同伴与教师的有效指导,让学生战胜学习上的困难,愉快的情绪体验使学生在讲题中获得快乐、提升、发展.
[1]中华人民共和国教育部.义务教育数学课程标准[M].北京:北京师范大学出版社,2011.
[2]佐藤学.教师的挑战宁静的课堂革命[M].钟启泉,译.上海:华东师范出版社,2012.
[3]李崇建.没有围墙的学校:体制外的学习天空[M].北京:首都师范大学出版社,2010.
2013年度江苏省博士后科研资助项目:新课程背景下数学教师专业素养研究——基于《教师专业标准》(1301129C);温州大学2013年教学改革项目:基于《教师专业标准》的《数学教学论》教学改革探索(13jg14);2014年温州大学面向基础教育重点课题:审视学生错题,深究课堂教学行为(WDZD201420).
