生物液膜振荡器中的振动共振

董 涛，李 军

（晋中学院化学化工学院，山西晋中030600）

（编辑 杨乐中）

Benzi等在研究周期循环的冰期气候系统时提出了随机共振（stochastic resonance，SR）的概念［1］.随机共振是指在非线性系统中，噪声在特定条件下可以提高系统对信号的响应.在特定的噪声强度下系统对微弱信号的响应达到极大值.几十年来，随机共振的研究一直是非线性科学研究的热点之一.2000年Landa等［2］发现了另一种与随机共振相类似的现象—振动共振（Vibrational resonance，VR）.振动共振是非线性系统在高、低两种不同频率信号作用下，以高频信号为调制信号，通过调节高频信号的幅值或频率来改变系统的动力学特性，使系统对低频信号的响应幅值达到极值［3］.这样的双频信号在激光［4］、声学［5］、神经系统科学［6］等领域的研究中的确存在，因此振动共振的研究具有重要的理论和实际应用价值.随着研究的深入，人们在双稳［7~9］、多稳［10~11］、可激［12~13］、神经网络［14~15］等系统都发现了振动共振现象.例如：在双稳系统中 Yang等的研究发现，时间延迟可以在单一系统以及耦合系统中诱导出振动共振［16~17］.Hu等在可激系统的研究中发现高频信号和时间延迟的协同作用可以使微弱的低频信号被强化［18］.Jeevarathinam C等人研究了多重时间延迟对单一杜芬振子振动共振以及耦合杜芬振子系统信号传递的影响，发现在合适的条件下信号可以无衰减地进行传播［19］；Yang等人则报道了过阻尼三势阱振子系统中振动双共振现象[20].

膜过程对于生命体维持正常的生命过程非常重要，在生命科学领域可兴奋膜的动力学研究一直以来备受重视.近年来，人工可兴奋膜作为简单、有效的模型常被用来模拟生物膜，以研究其动力学行为.这其中油/水液膜是最具希望的可兴奋生物膜的简单模型，考虑到动力学行为的相似性，油/水液膜常被用来模拟味觉和嗅觉细胞膜.迄今为止，在众多人工可兴奋膜型中，一般认为Yoshikawa小组提出的液膜振荡器模型是最完整、最成功的［21］.针对液膜振荡器，以前的研究工作大都集中在随机共振的相关研究上，例如：Xin小组研究发现在合适的条件下噪音可以诱导液膜振荡器发生随机共振和内信号随机共振现象［22~24］.Li等研究发现在两个耦合液膜振荡器中环境噪音也可以诱导出内信号随机共振［25］.然而，到目前为止，对液膜振荡器振动共振研究目前尚未见报道.笔者认为研究液膜振荡器中的振动共振行为有助于揭示味觉和嗅觉细胞探测微弱信号的内在机理.

1 模型和计算方法

本文采用Yoshikawa等提出的液膜振荡器模型［21~22］，其动力学方程式如下：

X，Y，Z分别代表表面活性剂，协同物和活性剂-协同物的加合物的浓度.下标b和i表示体系和油/水界面.G（Zi）是使体系表现出兴奋性的N型非线性函数，为使方程的解正定化，一般取：

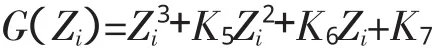
为研究高、低两种不同频率信号的引入对液膜振荡器振荡行为的影响，在Xb项加入高频和低频信号：（2）

这里方程（2）中的第二项表示加入的低频信号，振幅为A，频率为ω；第三项表示加入的高频信号，振幅为B，频率为Ω，一般Ω≫ω.

为了表征体系的振动共振，本文计算了输出信号（Zi）对输入低频信号频率（ω）的线性响应（Q）［26］，计算公式如下:

其中n是一个整数，方程（1-3）式是用步长为0.01时间单位的四阶龙格—库塔方法进行数值计算的.在计算中，持续时间为500时间单位.

2 结果与讨论

2.1 液膜振荡器中的振动共振

根据参考文献［22］，当体系参数 DX=2.0，DY=1.0，K1=1.4，K2=1.4，K3=20.0，K4=5.0，K5=-7.0，K6=3.30，K7=20.0，Yb=3.00；Xb=2.2-2.6时体系处于双稳区，这为选取控制参数的值提供了依据.首先选取Xb=2.475，以讨论体系处于双稳态时的振动共振规律.选取Ω=5；A=0.01，图1给出了低频信号频率ω取不同值时，线性响应Q随B的变化曲线.从图1(a)可以看出当ω=0.001时，随着B的增大，线性响应Q出现了多个峰，这表明发生了多重振动共振［27~29］，多重振动共振的出现说明体系的信号可以在不同的高频信号振幅处被放大；另外在其他低频频率下，如图1(b)ω=0.01，图1(c)ω=0.02时也观察到了类似的多重振动共振.对比图1(a)(b)(c)三个图，随着ω从0.001增大到0.02，多重共振峰对应的线性响应Q均值从4.6227降低到0.895左右，这说明随着ω增大，振动共振强度降低了，也就是说低频信号的频率越低，系统的振动共振强度越大.这与我们研究钙离子体系的振动双共振控制时的结论［27］以及林敏［30］等在研究双稳系统的振动共振时的结论相一致.

图1 低频信号频率ω取不同值时，线性响应Q随B的变化曲线Fig.1 Response(Q)of the system vs the amplitude(B)of the high frequency signal at various frequencies(ω)of low frequency signals(a)ω =0.001;(b)ω=0.01;(c)ω=0.02.parameters:DX=2.0,DY=1.0,K1=1.4,K2=1.4,K3=20.0,K4=5.0,K5=-7.0,K6=3.30,K7=20.0,Yb=3.00，Xb=2.475,Ω=5;A=0.01

固定参数ω=0.01；A=0.01，图2给出了高频信号频率Ω取不同值时，线性响应Q随B的变化曲线.如图所示，随着Ω从4.97增大到5.3，多重振动共振的峰均值从1.1162先增大到1.1170再减小到1.1130，这说明存在最佳的高频信号频率使得体系的多重振动共振达到最强.为了印证这一结论，我们进一步研究了线性响应Q随Ω的变化曲线，如图3所示（固定参数ω=0.01；A=0.01；B=70），可见，随着Ω增大，线性响应Q出现了多个峰，说明存在多个高频信号频率，使得体系的低频信号被放大.仿照前面的多重振动共振定义，可以把这种多重共振称为高频频率依赖的多重振动共振[10，16].那么，对于不同振幅或频率的低频信号，这种高频频率依赖的多重振动共振是否还会出现呢？因此我们首先固定参数ω=0.01；B=72，研究了低频信号振幅A取不同值时，线性响应Q随Ω的变化曲线（图4），从图上可以看出，不同的低频信号振幅，随着高频信号的频率逐渐增大，体系依然可以出现高频频率依赖的多重振动共振，而且随着信号振幅A从0.0001增大到0.1，高频频率依赖的多重振动共振曲线逐渐上移；高频信号频率越大，对应的共振峰上移的程度越大.这表明利用振动共振，体系对大振幅的低频信号的放大程度要比小振幅的低频信号大.这与大振幅的低频信号本身具有的能量大有关.这是因为在高频信号的振幅固定为B=72的条件下，通过振动共振的能量传递，高频信号传递给低频信号的能量是一样的，而振幅大的低频信号本身具有的能量大，两者叠加从而导致其被放大的倍数大.接着固定参数A=0.01；B=72研究了低频信号频率ω取不同值时，线性响应Q随Ω的变化曲线（图5）.从图5可见，ω=0.009，0.02时，体系都有高频频率依赖的多重振动共振发生.所不同的是，ω=0.009时的平均共振强度Q=1.6145，ω=0.02时的平均共振强度Q=0.08965，这说明ω=0.009时的平均共振强度要比ω=0.02的大，即频率越低，系统的高频频率依赖的多重振动共振强度越大.

2.2 负反馈机制对体系振动共振的影响

借鉴林敏等［31］在研究双稳体系随机共振的控制时提出的反馈机制，采用如图6所示的振动共振线性反馈控制原理研究反馈对体系振动共振的影响，这种反馈机制在我们研究钙离子体系的振动双共振控制时被证明是有效的［27］.与图6相对应的体系动力学方程变为：

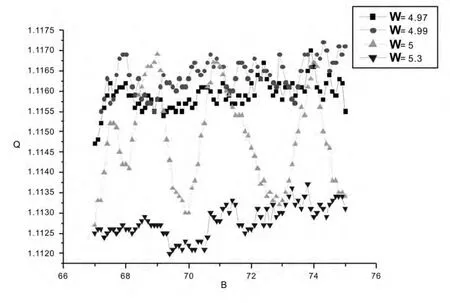
图2 高频信号频率Ω取不同值时，线性响应Q随B的变化曲线Fig.2 Response(Q)of the system vs the amplitude(B)of the high frequency signal at various frequencies(Ω)of high frequency signals ω=0.01.Other parameters are the same as those in Fig.1.

图3 线性响应Q随Ω的变化曲线Fig.3 Response(Q)of the system vs the frequencies(Ω)of high frequency signals ω=0.01;B=70.Other parameters are the same as those in Fig.1.Fig.1.

图4 低频信号振幅A取不同值时,线性响应Q随Ω的变化曲线Fig.4 Response(Q)of the system vs the frequencies(Ω)of the high frequency signal at various amplitudes(A)of low frequency signalsω=0.01;B=72.Other parameters are the same as those in Fig.1.

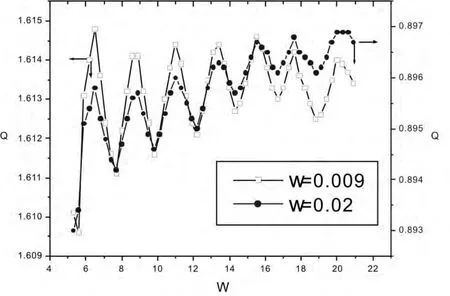
图5 低频信号频率ω取不同值时，线性响应Q随Ω的变化曲线Fig.5 Response(Q)of the system vs the frequencies(Ω)of the high frequency signal at various frequencies(ω)of low frequency signalsA=0.01;B=72.Other parameters are the same as those in Fig.1.

方程（4）中f（x）是反馈函数，反馈函数前的负号表示负反馈机制，取反馈函数f（x）=kXi，其中k是反馈参数.

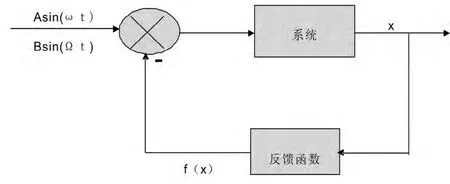
图6 振动共振的反馈控制示意图Fig.6 Scheme of the feedback control for vibrational resonance Asin(ωt)and Bsin(Ωt)are the low frequency and high frequency signals,respectively.parameters:A and B(the amplitude of signals),ω andΩ (the frequency of signals),f(x)is the feedback function,-denotes negative feedback

图7 是不同反馈参数k时，线性响应Q随B的变化曲线（固定参数ω=0.01；Ω=5；A=0.01）.从图上可以看出，不考虑反馈影响时（反馈参数k=0），体系表现出明显的多重振动共振，但随着负反馈参数k从0.2增大到1.6，体系的振动共振峰逐渐由多峰变为单峰；最终消失.这说明通过负反馈机制可以有效调节体系多重振动共振峰的个数.

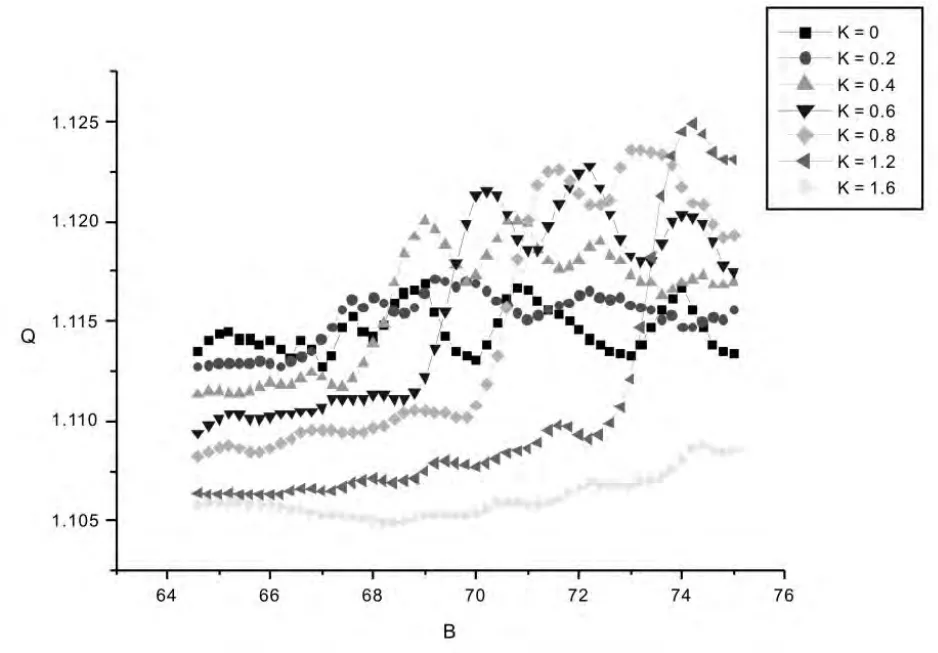
图7 不同反馈参数k时,线性响应Q随B的变化曲线Fig.7 Response(Q)of the system vs the amplitude(B)of the high frequency signal for the linear negative feedback at various feedback parameters(k)ω=0.01；Other parameters are the same as those in Fig.1.

图8 不同反馈参数k时,线性响应Q随Ω的变化曲线Fig.8 Response(Q)of the system vs the frequency(Ω)of the high frequency signal for the linear negativefeedback at various feedback parameters(k)ω=0.01;B=70;Other parameters are the same as those in Fig.1.

在固定参数ω=0.01；B=70；A=0.01条件下，笔者进一步研究了不同反馈参数k时，线性响应Q随Ω的变化曲线（图8）.从图8不难看出，与不加反馈时（k=0）相比，随着负反馈参数k从0.2增大到1.6，虽然体系的高频频率依赖的多重振动共振并没有消失，但其强度却逐渐减小，原因可能是负反馈对体系高频频率依赖的多重振动共振的影响机理不同于多重振动共振.

2.3 类频率共振强化的振动共振

Yao［8］等在研究过阻尼双稳体系的振动共振时发现：不同于传统的振动共振发生条件，高频信号频率要远远大于低频信号频率（Ω≫ω），在高频信号频率减小到低频信号频率大小（Ω=ω）时，合适的高频信号频率和高频信号振幅(Ω，B）下也能发生振动共振，而且其共振强度甚至比传统的振动共振强度更大.他们把这种振动共振称为频率共振强化的振动共振.由此可见对与振动共振研究，Ω≫ω不是充要条件，那么当低频信号频率逐渐增大到高频信号频率（ω=Ω）时，是否还会有振动共振发生呢？图9是线性响应Q随B的变化曲线（ω=Ω=5；A=0.01），从图上可见明显的峰形曲线，表明在ω=Ω=5的条件下同样可以发生振动共振，为了和Yao等报道的振动共振相区别，笔者认为可以把这种振动共振称为类频率共振强化的振动共振.类频率共振强化的振动共振现象的发现进一步扩宽了体系发生振动共振的条件.

3 结论

本文研究了生物液膜振荡器在高、低两种不同频率信号作用下所产生的振动共振现象.结果表明：体系线性响应Q随B的变化出现了多个峰，即发生了多重振动共振，且低频信号的频率越低，系统的振动共振强度越大.另外，存在最佳的高频信号频率使得体系的多重振动共振达到最强.而且体系线性响应Q随Ω的变化可以发生高频频率依赖的多重振动共振；对不同振幅或频率的低频信号，利用高频频率依赖的多重振动共振，体系对振幅大的低频信号的放大程度要比振幅小的低频信号大；低频信号频率越低，系统的高频频率依赖的多重振动共振强度越大.还讨论了负反馈机制对体系振动共振的影响，通过负反馈机制可以有效调节体系多重振动共振峰的个数；负反馈对体系高频频率依赖的多重振动共振的影响则主要体现在影响其强度而对其共振峰的个数没有影响.当ω=Ω时，体系可以发生类频率共振强化的振动共振.笔者期望所得结果有助于更好的理解味觉和嗅觉细胞感受外界信号刺激的机理，并为其它双谐波作用下的非线性体系动力学研究提供借鉴和参考.

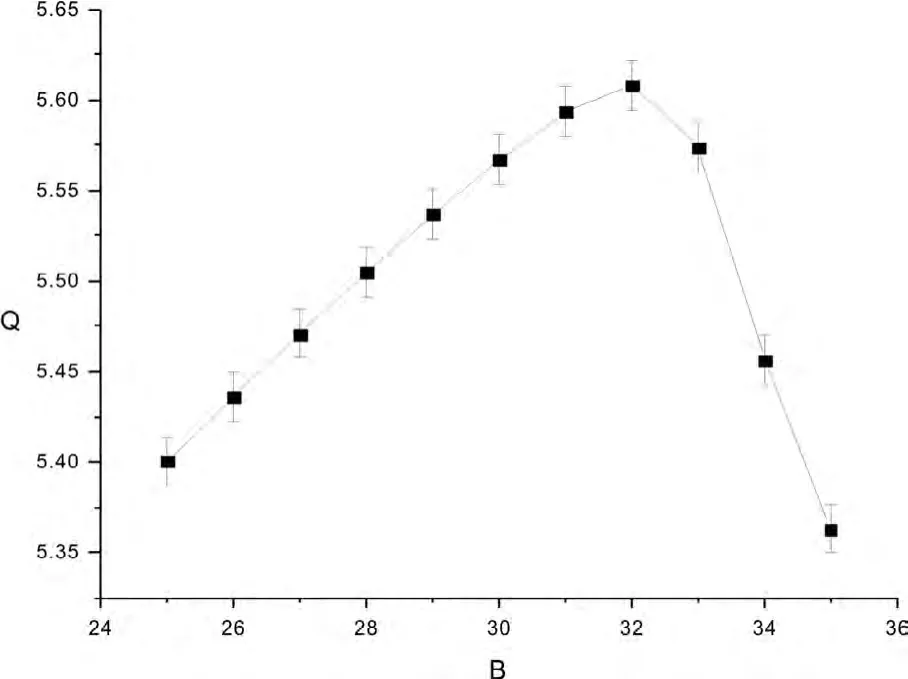
图9 线性响应Q随B的变化曲线Fig.9 Response(Q)of the system vs the amplitude(B)of the high frequency signal.ω=Ω=5;Other parameters are the same as those in Fig.1.

［1］Benzi R，Sutera A，Vulpiana A.The mechanism of stochastic resonance［J］.Journal of Physics A:Mathematical and General，1981（14）：453~457.

［2］Landa PS，McClintock PVE.Vibrational resonance［J］.JPhys A：Math Gen，2000，33：L433~L438.

［3］林敏，黄咏梅.基于振动共振的随机共振控制.物理学报［J］.2007，56（11）：6173~6177.

［4］Volkov EI，Ullner E，Zaikin A A，et al.Oscillatory amplification of stochastic resonance in excitable systems［J］.Physical Review E，2003，68（2）：026214-1~026214-7.

［5］Maksimov AO.On thesubharmonic emission of gasbubblesunder two-frequency excitation［J］.Ultrasonics，1997，35（1）：79~86.

［6］Victor JD，Conte M M.Two-frequency analysis of interactions elicited by Vernier stimuli［J］.Visual neuroscience，2000，17（6）：959~973.

［7］Blekhman I.I，Landa PS.Conjugate resonances and bifurcations in nonlinear systems under biharmonical excitation［J］.Int J Non-Linear Mech，2004（39）：421~426.

［8］Yao C，Liu Y，Zhan M.Frequency-resonance-enhanced vibrational resonance in bistablesystems［J］.Physical Review E，2011，83（6）：061122-1~061122-6.

［9］Yao C，Zhan M.Signal transmission by vibrational resonancein one-way coupled bistable systems［J］.Physical Review E，2010，81（6）：061129-1~061129-8.

［10］Rajasekar S，Abirami K，Sanjuan M A F.Novel vibrational resonance in multistable systems［J］.Chaos：An Interdisciplinary Journal of Nonlinear Science，2011，21（3）：033106-1~033106-7.

［11］Yang JH，Liu X B.Controlling vibrational resonance in a multistable system by time delay［J］.Chaos，2010，20（3）：033124-1~033124-7.

［12］Zhao J，Deng B，Wei X，et al.Dynamical encoding of winnerless competition network induced by vibrational resonance［J］.Control and Decision Conference（CCDC），2012 24th Chinese.IEEE，2012：1167~1171.

［13］Yang L，Liu W，Yi M，et al.Vibrational resonance induced by transition of phase-locking modes in excitable systems［J］.Physical Review E，2012，86（1）：016209-1~016209-7.

［14］Qin Y，Wang J，Men C，et al.Vibrational resonance in feedforward network［J］.Chaos：An Interdisciplinary Journal of Nonlinear Science，2011，21（2）：023133-1~023133-8.

［15］Xue M，Wang J，Deng B，et al.Vibrational resonancein feedforward neuronal network with unreliablesynapses［J］.The European Physical Journal B，2013，86（4）：1~9.

［16］Yang JH，Liu X B.Delay induces quasi-periodic vibrational resonance.Journal of physics［J］.A，Mathematical and theoretical，2010，43（12）：122001-1~122001-7.

［17］Yang JH，Liu X B.Delay-improved signal propagation in globally coupled bistable systems［J］.Physica Scripta，2011，83(6)：065008-1~065008-7.

［18］Hu D，Yang J，Liu X.Delay-induced vibrational multiresonance in FitzHugh–Nagumo system［J］.Communications in Nonlinear Scienceand Numerical Simulation，2012，17（2）：1031~1035.

［19］Jeevarathinam C，Rajasekar S，Sanjuán M A F.Effect of multiple time-delay on vibrational resonance［J］.Chaos，2013(23)：013136-1~013136-11.

［20］Yang Y，Wang C.Theory and nuberics of double-vibrational resonance in the overdamped oscillator［J］.Chinese JPhys，2013，51（4）：728~737.

［21］Yoshikawa K，Makino M，Nakata S，et al.Non-linear characteristicsof lipid monolayersin relation to the ability to self-organize［J］.Thin Solid Films，1989，180（1）：117~121.

［22］Zuo X，Hou Z，Xin H.Stochastic resonance in liquid membrane oscillator［J］.The Journal of chemical physics，1998，109：6063~6066.

［23］Zhong S，Xin H.Noise-induced oscillations and internal stochastic resonance in a model of excitable biomembrane［J］.Chemical Physics Letters，2000，321（3）：309~314.

［24］Qi F，Xin H.Stochastic resonance induced by fluctuation in liquid membrane oscillator without input signals［J］.Biophysical chemistry，2001，90（2）：175~182.

［25］Li Q S，Li Y P.Internal stochastic resonance in two coupled liquid membrane oscillators［J］.Physical Review E，2004，69（3）：031109-1~031109-7.

［26］Ullner E，Zaikin A，Bascones R，Garcia-Ojalvo J，Kurths J.Vibrational resonance and vibrational propagation in excitable systems［J］.Phys Lett A，2003，312：348~354.

［27］施建成，董涛.钙离子体系的振动双共振控制［J］.Acta Phys.Chim.Sin，2010，26（2）：487~494.

［28］张路，谢天婷，罗懋康.双频信号驱动含分数阶内、外阻尼 Duffing振子的振动共振［J］.物理学报，2014，63（1）：010506-1~010506-7.

［29］Jeyakumari S，Chinnathambi V，Rajasekar S，et al.Vibrational resonance in an asymmetric Duffing oscillator［J］.International Journal of Bifurcation and Chaos，2011，21（01）：275~286.

［30］林敏，黄咏梅.双稳系统的振动共振及特性分析［J］.振动与冲击，2007，26（12）：151~153.

［31］林敏，黄咏梅，方利民.双稳系统随机共振的反馈控制［J］.物理学报，2008，57（04）：2041~2047.