带有丢包及网络切换的分布式H∞滤波系统的性能分析

马秀莉，刘 博

（1.晋中学院数学学院，山西晋中030619；2.山西大学数学科学学院，山西太原030006）

（编辑 郭继荣）

传感器网络是由大量的传感器通过网络连接而组成的一个整体系统.每个传感器具备采样、计算以及和相邻节点传输信息的功能.这些传感器通过网络连接并互相协作，从而完成对目标系统的估计.近年来，传感器网络的滤波问题是控制领域的一个热点问题，并有很多实际应用，如环境监测、监督系统、工业自动化，等等[1~2].

对于传感器网络的分布式滤波问题，现有结果主要集中于对分布式Kalman滤波问题的研究.对于分布式H∞滤波问题，相关研究结果较少[3~5].本文研究了基于传感器网络的分布式H∞滤波系统的性能分析。文章给出了两类传输通道的数据丢包模型，建立了数据丢包和网络结构的任意切换情形下的滤波器的模型，得到了全局误差系统，并给出了全局误差系统的H∞性能分析.

1 问题给出

考虑非线性连续时间系统

应用传感器网络对系统信号进行估计.在此考虑两种网络诱导因素的影响：1）传感器网络之间传输信号的丢包；2）传感器网络结构的任意切换.对于一个有N个节点的传感器网络，至多有2NN-（）1种网络结构.因而假设网络结构在一组有限的集合内任意切换.h为采样间隔，网络结构切换的时间序列记为 k1h，k2h，…，klh，…，在区间 [sh ， kh]内网络切换的次数记为Nsw[s，k ]，则在 [sh ， kh]内网络切换的频率表示为

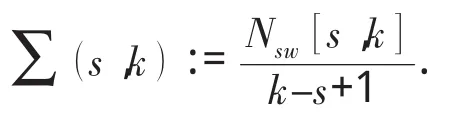
考虑从对象到滤波器的网络和从滤波器到滤波器的网络中都存在丢包的情形。滤波器i的测量模型为

在此yi（kh）为测量向量,v（k ）∈l2[0，∞）为测量噪音，Ci，Di定常矩阵,βi为相互独立的服从伯努利分布的随即向量，其取值为0或1的概率为

滤波器i的相邻节点接收滤波器i的信号，其模型为

在此αi之间相互独立，且αi与相互独立.

在节点i处，对kh≤t<（k+1）h，相对应于网络结构由（2），（3），滤波器模型为

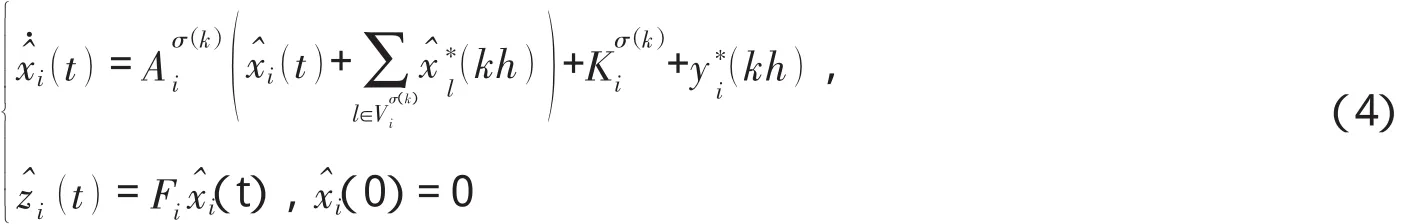
在此，xˆi（）t 为滤波器 i的状态；zˆi（）t为滤波器i对z（）t的估计，xˆi（0）＝0为初始向量，Aσ（）ki，Kσ（）ki，Fi设计的滤波器参数.记

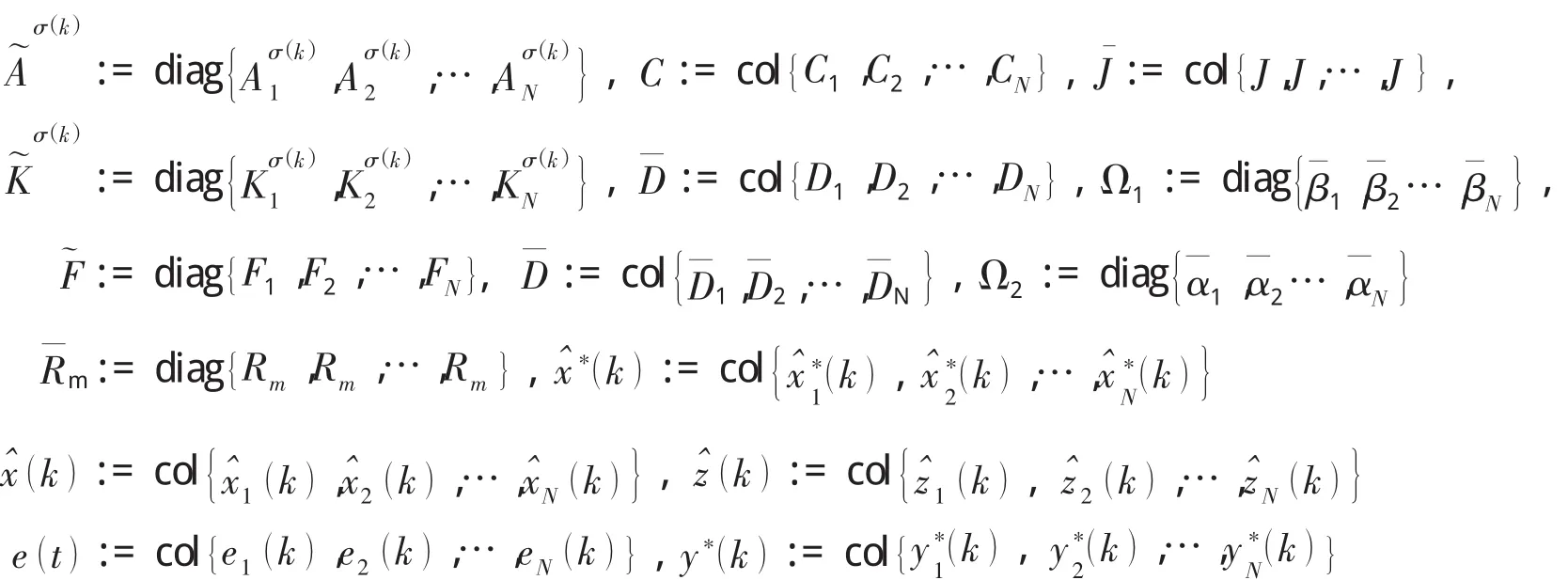
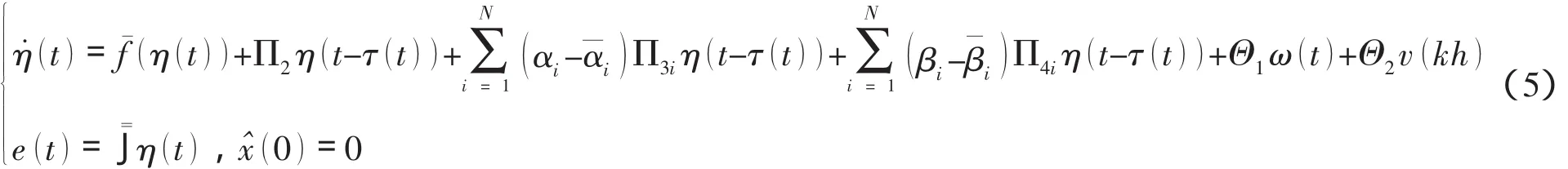
其中

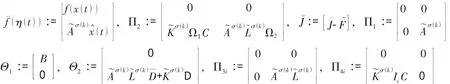
基于系统（5），分布式H∞滤波问题描述如下：

分布式H∞滤波问题:设计切换的分布式H∞滤波器参数使得以下条件成立：

2.零初始条件下，滤波误差系统（5）满足H∞性能γ

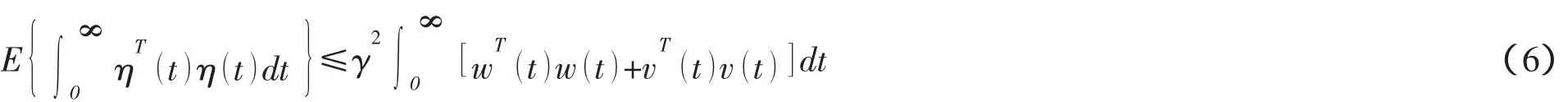
2 H∞性能分析

考虑系统（5）的H∞性能分析，有如下结论

定理1给定标量γ0＞0，μ＞1，1＜ø＜e，α＞0,如果网络结构的切换率满足，并且存在正定矩阵 Pm＞0，Qm＞0，Rm＞0，m=1，2，…，M 及实矩阵 S 满足如下不等式

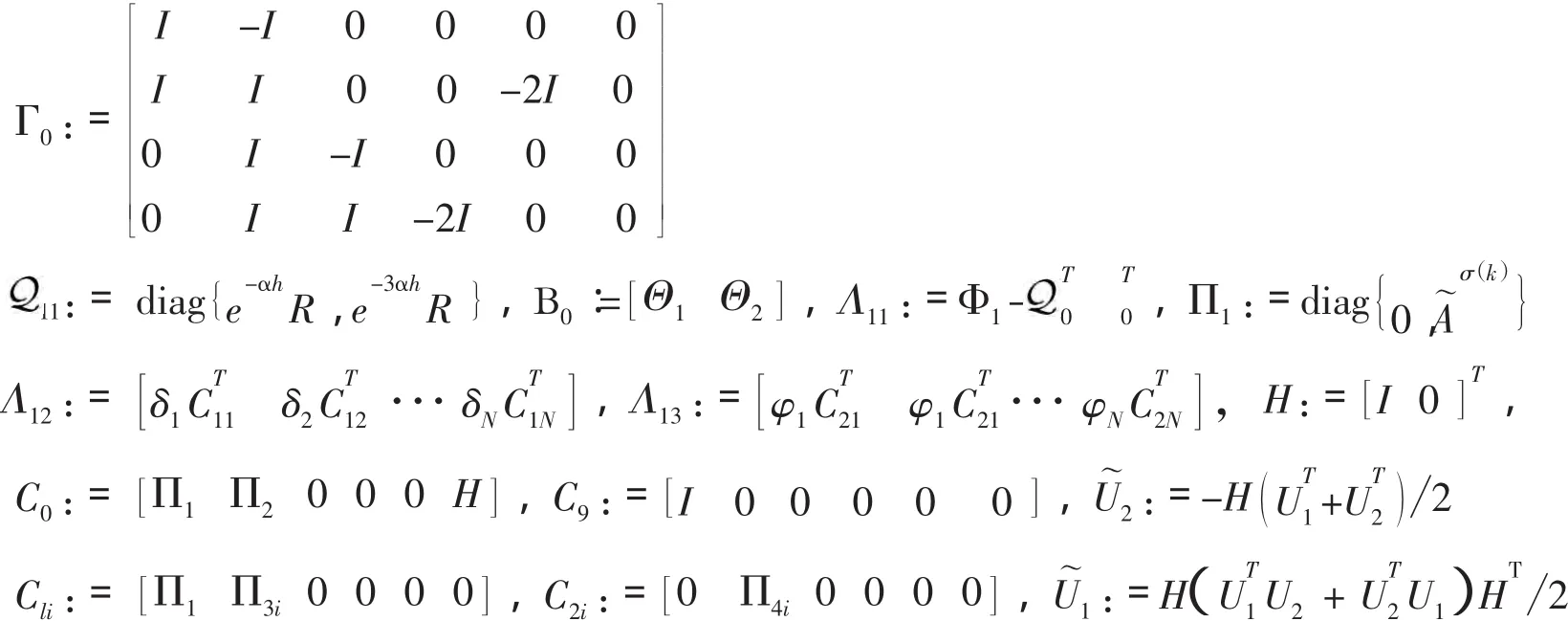
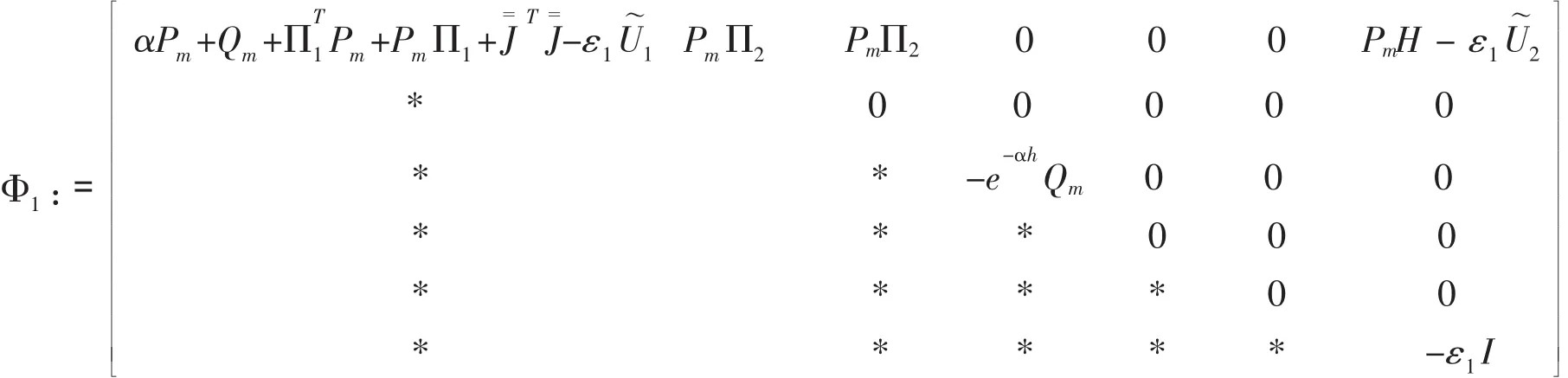
则分布式滤波误差系统（5）是指数均方稳定的且满足H∞性能γ0.

证明：由于篇幅所限，证明过程略.

本文研究了传感器网络的分布式H∞滤波问题.考虑了数据丢包、网络结构任意切换两类网络因素的影响，建立了滤波误差系统的模型，并应用Lyapunov泛函方法，给出了滤波误差系统的性能分析.由于篇幅所限，分布式H∞滤波器的设计问题，以及数值仿真部分略去.

［1］J.P.Hespanha,,P.Naghshtabrizi，Y.Xu.Asurvey of recent resultsin networked control systems［J］.Proceedings of the IEEE，2007，95（1）：138~162.

［2］I.F.Akyildiz，W.Su，Y.Sankarasubramaniamand E.Cayirci，Wireless sensor networks:a survey［J］.Computer Networks，2002，38（4）：393~422.

［3］B.Shen，Z.Wang，Y.S.Huang.Distributed H∞Consensus Filtering in Sensor Networks with Multiple Missing Measurements:The Finite-horizon Case［J］.Automatica，2010，46（10）：1682~1688.

［4］H.Dong，J.Lam，H.Gao.Distributed H∞Filtering for Repeated Scalar Nonlinear Systems with Random Packet Lossesin Sensor Networks［J］.International Journal of Systems Science，2011，42（9）：1507~1519.

［5］D.Zhang，L.Yu，H.Song，Q.Wang.Distributed H∞Filteringfor Sensor Networks with Switching Topology［J］.International Journal of Systems Science［J］.2013，44（11）：2104~2118.

［6］A.Seuret，F.Gouaisbaut.“Wirtinger-based integral inequality：Application to time-delaysystems［J］.Automatica 2013，49（9）：2860~2866.

［7］K.Liu，E.Fridman.Wirtinger’sinequality and Lyapunov-based sampled-datastabilization［J］.Automatica，2012，48（1）：102~108.