利用RBF神经网络实现三角网格模型的孔洞修补

余水晶

(海南省技师学院,海南 海口 571100)

利用RBF神经网络实现三角网格模型的孔洞修补

余水晶

(海南省技师学院,海南 海口 571100)

本文提出一种利用径向基函数(RBF)神经网络实现三角网格曲面孔洞的修补算法,首先用孔洞边界周围的三角片顶点作为学习样本训练RBF网络,然后对孔洞进行平面填充,获得新增三角片的顶点,最后用已训练好的RBF网络将其优化,实现三角网格孔洞的修补。

神经网络;逆向工程;孔洞修补

逆向工程(Reverse Engineering)是利用实物模型测得的数据构造CAD模型,继而进行分析制造。在逆向工程中,三角网格模型是一种非常通用的数据模型。利用测量设备可获得实体的点云数据,然后对点云数据进行三角网格化处理就可得到三角网格模型。由于测量设备及模型特征等的限制,生成的点云数据常因信息量不足而产生孔洞,从而造成三角网格重建后的模型出现孔洞。孔洞的出现,使建模的质量受到严重影响,不利于对模型进行有限元分析、快速原型制造等后续处理。因此,孔洞修补在逆向工程建模中是一个重要的数据处理步骤。

一些学者利用BP神经网络实现了孔洞的修补,但BP神经网络的构建复杂,参数确定工作量大,且网络训练结果不稳定。径向基函数(RBF)神经网络是近几年来应用较多的一种神经网络模型。RBF网络构建简单,训练时间短,网络结构和参数调整方便,具有较好的局部逼近能力,且网络训练结果稳定。本文将RBF神经网络应用于三角网格模型孔洞修补工作,取得了较好的效果。

1 径向基函数(RBF)神经网络

RBF神经网络在分类、学习速度、函数逼近能力等方面均优于BP神经网络。Hornik［1］证明了单隐层的RBF网络可以逼近任意的非线性函数。

1.1 神经网络结构

RBF网络是由输入层、隐层和输出层组成的三层前向神经网络。隐层节点由高斯核函数构成,输入层到隐层的变化是非线性的,而隐层到输出层则是简单的线性关系。假设N、M、L分别是网络的输入节点数、隐层节点数以及输出节点数。隐层常用的函数形式是高斯核函数。

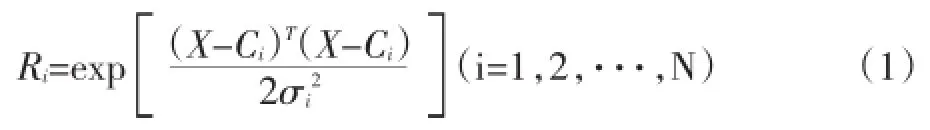
其中X=(x1,x2,…,xM)T

X——输入矢量

Ri——第i个隐层节点的输出

Ci——隐层第i个高斯单元的中心矢量

σi——第i个中心矢量的半径

RBF神经网络的输出可表示为：

其中Wj——隐层到输出层的权值

1.2 神经网络的学习

RBF神经网络的学习算法主要分两步：首先,根据输入样本确定高斯核函数的中心Ci和半径σi,可采用K一均值聚类算法；其次,求出隐层和输出层之间的权值Wj,可采用递推最小二乘法(RLS)计算。

2 利用RBF神经网络实现三角网格曲面的孔洞修补

本文采用的孔洞修补算法主要分为三步：首先,检测出三角网格模型的孔洞,并采集孔洞周围的三角片顶点,用采集到的三角片顶点作为学习样本训练RBF神经网络；接着,对孔洞多边形进行平面填充,获得新增三角片的顶点；最后,用已训练好的RBF神经网络使其优化,将平面填充后三角片顶点向三维空间映射,实现三角网格孔洞的修补。

2.1 三角网格孔洞检测

对于封闭结构的三角网格模型,可利用拓扑关系搜索到孔洞的边界［2］：先找到一条仅属于一个三角片的边,则该边即为构成孔洞多边形界边,称之为边界边。以这条边界边作为种子边来寻找其相邻的边界边,搜索完整的三角网格模型,最终找到由边界边首尾相连组成的封闭空间多边形,则该多边形为模型的一个孔洞。

2.2 特征面的填充

特征面的填充实际上是一个投影多边形平面三角化的过程。本文采用如下算法［3］:①用孔洞边界顶点构造一最小二乘平面,并以孔洞多边形的重心为原点,在最小二乘平面上任取两个相互垂直的单位向量与该平面的法矢量建立一局部坐标系。②构造新的三角片。每次寻找投影多边形夹角最小的一对邻边,构造新的三角片；更新孔洞多边形,直至新增三角片覆盖整个孔洞。③将新增三角片的顶点由局部坐标系下的坐标变换到全局坐标系下。

2.3 训练样本的采集

采集需要修补的孔洞多边形的顶点,以及其相邻几层(一般为三层)的三角片的顶点作为学习样本训练RBF神经网络,使其能表示孔洞周围曲面的函数形式。本文采用的方法如下：step1.定义K为孔洞多边形顶点组成的集合,在K中任取一三角片的顶点,寻找与其相邻的三角片顶点；step2.将不在集合K中的顶点放入另一集合中,当搜索完K中顶点后,N便为孔洞多边形向外扩展的第一层三角片的顶点；step3.重复step1和step2,直至向外采集达到所设定的层数为止。

2.4 利用RBF神经网络实现孔洞的修补

在三维空间中,曲面可用函数关系式z=f(x,y)表示,训练好的RBF网络能精确映射样本函数z=f(x,y)。用采集到的孔洞多边形顶点及相邻三角片顶点的x、y分量作为网络输入,z分量作为目标输出,训练网络,使其能映射孔洞曲面函数z=f(x,y)。特征面的填充实现了对孔洞多边形的平面三角网格化过程,而孔洞修补的主要原理是通过建立空间孔洞多边形的特征面来完成孔洞多边形的填充。在允许的误差范围内,将新增三角片顶点坐标的x、y分量输入到已训练好的RBF网络,则可认为RBF网络的输出就是新增三角片顶点的z分量。这样,就可获得孔洞区域内全局坐标系下新增三角片顶点的坐标,实现将平面填充后三角片顶点向三维映射的目的,从而完成了三角网格孔洞的修补。

3 应用实例

为了验证算法的有效性,用本文的算法对一具有真实孔洞的鸭子模型三角网格曲面,如图1所示,进行了修补,修补后其效果图如图2所示。

图1

图2

4 结论

本文提出一种利用RBF神经网络实现三角网格孔洞的修补算法。利用孔洞边界周围的三角片顶点作为训练样本训练RBF神经网络,然后用已训练好的网络将平面填充获得的新增三角片顶点映射到三维空间,最终实现孔洞的修补。

［1］Horni K.Approximation capabilities of multiplayer feed一forward network［J］.Networks,1991,4(2):251一257.

［2］王宏涛,张丽艳,李忠文,等.基于RBF神经网络的三角网格曲面孔洞修补［J］.中国机械工程,2005,16(12): 2072一2075.

［3］刘德平,余水晶,王莹莹.基于最小二乘支持向量机的三角网格修补算法［J］.计算机集成制造系统,2009,15(9): 1867一1871.

Using RBF Neural Network to RealiZe the Hole RePair of Triangular Mesh Model

Yu Shuijing
(Hainan Technician College,Haikou Hainan 571100)

This paper presents a algorithm for the reconstruction of triangular mesh surfaces using the radial basis function(RBF)neural network.Firstly,the RBF network is trained by using the triangle mesh vertices around the hole boundary as studying samples.Then the holes are filled in the hole,and the added vertices are obtained.Finally, thetrained RBF network is used to optimize the mesh,and realize the repair of triangular mesh.

neural network;reverse engineering;holerepair

TP391

A

1003一5168(2015)07一0030一2

2015一6一10

余水晶(1983―),男,硕士研究生,研究方向:逆向工程,先进制造技术。