气浮筒型基础结构垂荡水动力系数研究❋

丁红岩， 石建超， 张浦阳❋❋， 刘宪庆

(1. 天津大学水利工程仿真与安全国家重点实验室，天津 300072；2. 滨海土木工程结构与安全教育部重点实验室(天津大学)，天津 300072；3.天津大学建筑工程学院，天津 300072)



研究简报

气浮筒型基础结构垂荡水动力系数研究❋

丁红岩1,2,3， 石建超3， 张浦阳1,2,3❋❋， 刘宪庆3

(1. 天津大学水利工程仿真与安全国家重点实验室，天津 300072；2. 滨海土木工程结构与安全教育部重点实验室(天津大学)，天津 300072；3.天津大学建筑工程学院，天津 300072)

筒型基础作为一种新型的基础形式已经广泛的应用于海洋资源的开发。在筒型基础作为边际油田开发的基础形式的背景下，基于 “大尺度筒型基础的浮运拖航”关键技术，本文对筒型基础在海洋环境荷载作用下的运动响应进行了相应的研究和分析。通过引入考虑气垫影响的无因次参数α处理筒内气水界面的非线性边界条件，基于三维势流理论、采用半解析法的特征函数展开并匹配渐进法，得到气浮筒型基础结构的垂荡下辐射运动的基本规律。还以CBF-3-150海上风电复合筒型基础为例，应用上述理论，运用MATLAB编程平台编制计算程序，求解得出该结构的垂荡水动力系数。

筒型基础； 气浮结构； 垂荡； 水动力系数； 非线性

筒型基础是一种新型的风机基础形式，具有气浮拖航、负压下沉和重复利用的优势。在浅海区水深不足，筒型基础可通过充气浮运，利用驳船拖到指定地点，然后借助负压进行下沉[1-2]。“大尺度筒型基础的浮运拖航”是推广近海风电场快速建造的关键技术之一，因此，海洋环境荷载作用下筒型基础浮运拖航中的运动响应成为研究的重点。天津大学丁红岩、张浦阳等建立了样机并进行了相关拖航研究[3-7]。筒型基础在拖航运动过程中，受到拖轮牵引力的作用主要进行升沉、横摇与纵摇运动，不仅基础结构本身运动，而且接近基础或者基础前面的一定量的水也随基础结构一起运动，跟随基础一起运动的这部分水的质量称为附加质量。且由于水和结构之间的黏滞效应，结构的振动也伴随着相应的辐射阻尼，而附加质量和辐射阻尼系数在大尺度筒型基础的振动中起到重要的作用。

国内外对附加质量的研究始于20世纪三四十年代，对于规则形状在无穷域中的附加质量的推导都基本上得到了解析解[8]；Garretz在1971年得到了考虑散射影响的表面波下作用在船坞上的水平、垂直力及其力矩[9]；Yeung[10]和Sabuncu[11]分别在1980和1981年独自推导了有限水深下单一圆柱形浮体在垂荡、摇摆方向的附加质量以及阻尼系数的理论值；1992年，Landweber L和Shahshahan A[12]对圆柱在半无限域中振动时考虑圆柱与封闭端的不同距离所对应的圆柱的附加质量系数进行了研究；2001年，David Clarke[13]对圆柱在浅水中的附加质量的问题进行了研究，得到了浅水中圆柱体的附加质量系数的公式并对底部条件对附加质量系数的影响进行了分析；1990年，宗智、黄鼎良应用匹配渐进法对贴近水底的矩形柱体在浅水中的水动力系数进行了研究；1995年，于洋、周树信对浅水中细长体的附加质量进行了研究，给出了水深与吃水深比小于2.0时柱体在横荡和升沉2个自由度上的附加质量的计算方法；2007年，马烨、单雪雄利用CFD无粘性流体模型以及动网格技术,数值模拟物体的匀变速运动，并根据其受力方程得到物体六自由度运动情况下的附加质量[14]； 2009年，黄旋等人基于在数值水洞中作摇荡运动物体的水动力系数进行了研究，研究的结果可以用来预测带空泡运动细长体的附加质量[15]。在已有的研究中，对于气浮筒型基础结构的水动力系数的取值可以参考的理论和研究资料还是相对较少[16]。本文通过引入考虑气垫影响的无因次参数处理筒内气水界面的非线性边界条件，基于三维势流理论采用半解析法的特征函数展开并匹配渐进法，对气浮筒型基础结构的垂荡下辐射运动的基本规律进行研究，为工程中参数的选取提供参考，也为后续的计算结构在波浪下的响应提供理论基础。

1 理论部分

在流体中，有一个半径为a，吃水为T的垂直气浮筒型基础结构在水面上做频率为ω的小振幅简谐振荡运动。由于筒型基础结构的轴对称性，只需要考虑3种振荡运动模态，即沿着oz的垂荡，沿着ox轴的横荡运动以及绕着oy轴的横摇运动。取柱坐标系orθz，使得oz轴垂直向上且与圆柱浮体中心轴重合，orθ平面与未扰动静水面重合(见图1)。

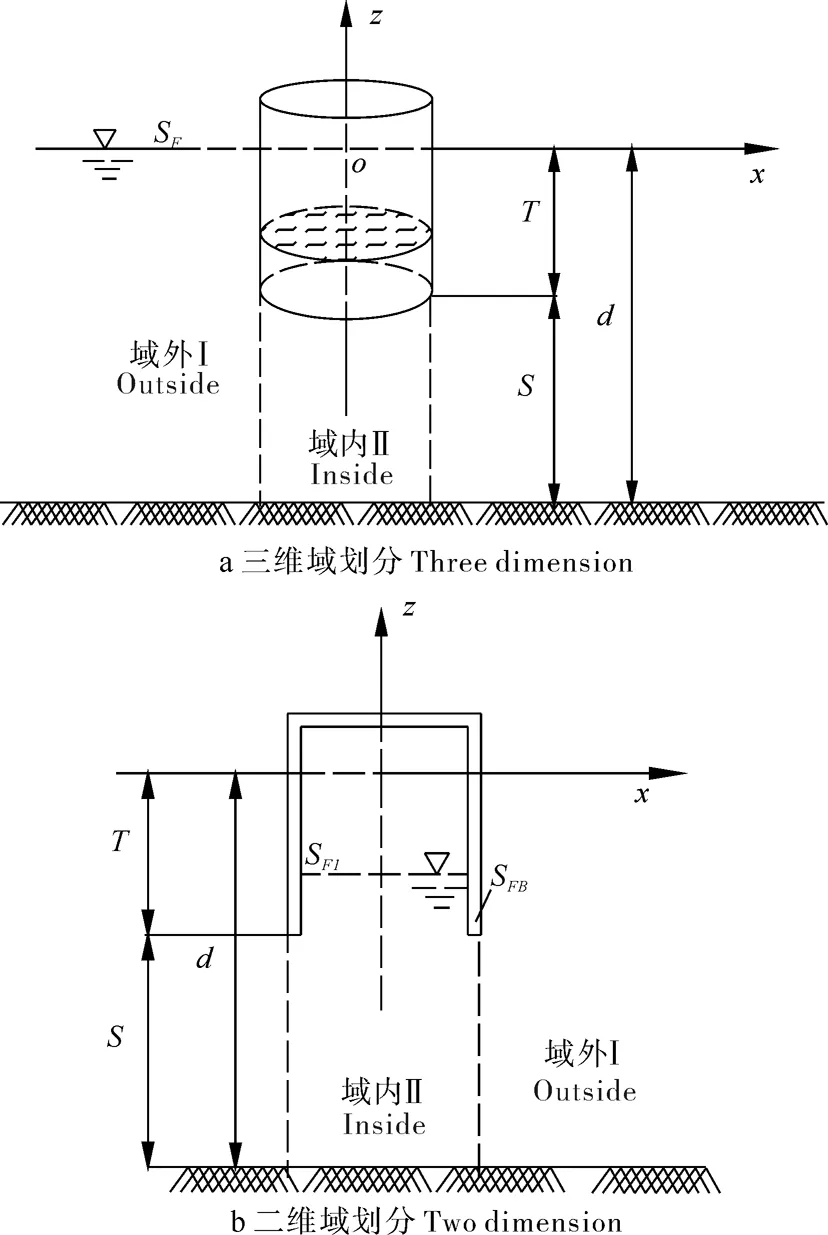
图1 气浮筒型基础流域划分

设流体是理想和不可压缩的，流体是无旋的，气浮筒型基础浮体振荡运动引起的流场可以用速度势ΦR(r,θ,z,t)来描述。由于气浮筒型基础的振荡运动是小振幅的，因此可以在线性势流理论框架中，速度势ΦR可以分解为垂荡速度势、横荡速度势和横摇速度势的线性叠加，如下：

ΦR(r,θ,z,t)=

ΦR1(r,θ,z,t)+ΦR3(r,θ,z,t)+ΦR5(r,θ,z,t)=

(1)

式中：φR1为横荡速度势的空间部分；φR3为垂荡速度势空间部分；φR5为横摇速度势空间部分。

对应不同的运动模态的辐射速度势φRj均满足Laplace方程、自由表面条件、水底边界条件和无限远辐射条件如下：

(2)

式中：v=-w2/g；k为气浮力折减系数；计算中对倾斜状态的参量进行修正。

对于内域II中，SFI处的动力学边界条件和运动学边界条件为：

pc=-ρg(Tc+Ξ) 动力学边界条件；

(3)

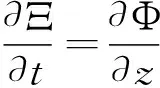
(4)

式中：pc为筒内气体压力；Tc为筒内气-水交界面处的自由表面的平均位置；Ξ为相对于Tc的高程。

取公式(3)的时间导数，得到：

(5)

假设气垫内的压力变化满足玻意耳-马略特定律，得到：

(6)

式中：pcs为气垫静压力，pcs=-ρgTc+pa，pa为大气压力；Δp为气垫气压的变化量，Δp=pc-pcs；Vcs为气垫平均体积； ΔV为为气垫体积变化量；κ为绝热系数，当满足玻意耳-马略特定律时，对于空气κ=1.0。

将式(6)代入式(5)得到：

(7)

从而，根据筒型基础运动和自由表面高程得到的相关的体积变化ΔV如下：

(8)

式中：ξ为气浮结构的竖向位移，初始时刻位于交界面SFI；Ξ为相对于Tc的高程。

则内部自由表面条件最终变为：

(9)

对于垂荡和横摇运动，频域内的线性化的自由表面条件为：

(10)

2 垂荡解析

对于单个气浮筒型基础结构的垂荡运动，由于筒型基础结构的轴对称性以及整个流场的轴对称性，所以对速度势的求解和角θ无关，可以得到垂荡速度势的表达式为：

(11)

从以上分析的垂荡运动满足的边界条件来看，在内域和外域内，对垂荡速度势仅仅采用只考虑零阶傅立叶模态的特征函数进行展开。

对于外域I中的速度势可以表示为：

(12)

(13)

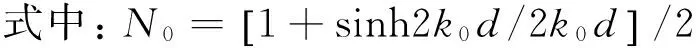
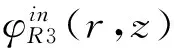
(14)

对于单位振幅的垂荡运动，在内部自由表面条件为：

(15)

(16)

(17)

式中：Gn(βnz)为在区间[-d,-T]正交化的函数，定义为：

(18)

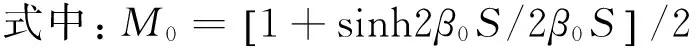
对于特解，通过观察可以得到：

(19)

将(14)代入交界面处的边界条件(10)得到：

(20)

将(10)和(20)代入(14)得到内域速度势的表达式：

(21)

为了得到Cm和Dn，在r=a处，根据速度势的连续条件，利用Gn(λn,z)的正交性得到：

(22)

将式(12)及式(21)带入式(22)计算可得：

(23)

式中：

(24)

(25)

(26)

根据r=a处的速度连续性条件以及外域特征函数Zm(kmz)的正交性，得到：

(27)

由于：

(28)

根据结构在水面上的摇摆中心点坐标得到：

(29)

式中：

(30)

(31)

(32)

联立得到关于未知常数Cm和Dn的无穷阶方程组，考虑各式中Bessel函数的数学特性，可以在保证求解精度的基础上适当截断来求解有限阶的方程组，节省计算资源。

根据Bernoulli方程，作用在结构上的力可以由体表面上的压力积分得到。如参考文献[17]所示，对于辐射问题中力可以用如下形式表示：

Fij=-ω2μij+iωλij=

(33)

式中：μij和λij是附加质量系数和阻尼系数；ni为单位内法线方向。

对于垂荡运动，通过推导可以得到附加质量μ33和阻尼系数λ33：

(34)

3 算例

算例选取CBF-3-150海上风电复合筒型基础进行分析。将坐标原点选为筒顶部圆心位置，作为海上风机基础的大尺度筒型基础,CBF-3-150拖航总质量为2200t，重心位置(0,0,1.91m)。实际拖航模型如图2所示。由于海洋波浪的周期主要集中在4～20s之间，其对应的频率范围为0.05～0.25Hz，所以通过上述理论计算在圆频率为0.05～1.0rad/s内的垂荡运动的水动力系数能够反映结构垂荡响应的规律。

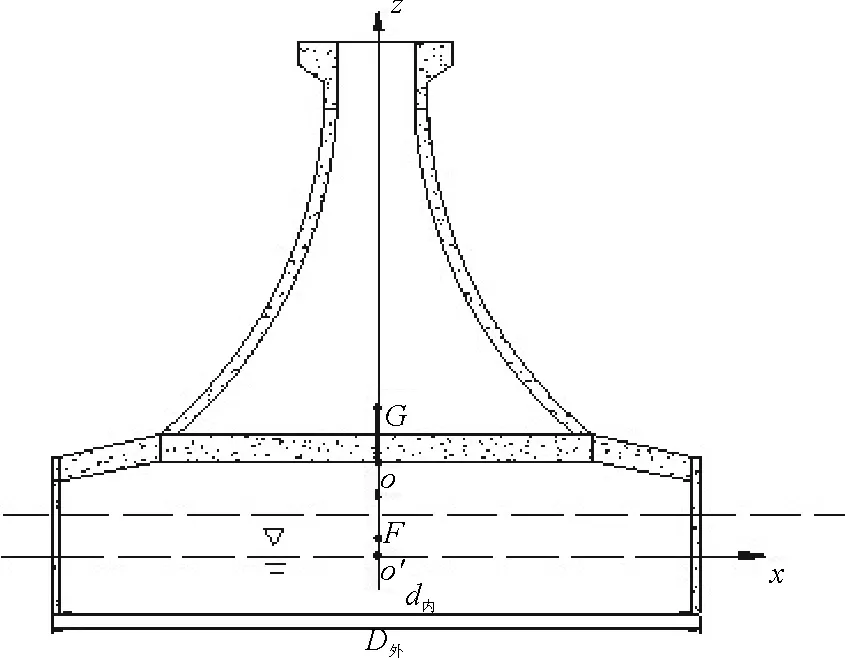
图2 算例模型示意图Fig.2 The actual model

应用上述理论基于MATLAB编程平台编制计算程序，求解结构的水动力系数，对于横荡、垂荡和纵摇的附加质量分别以ρπRT2、ρπR2T和ρπR3T2进行无因次化，对于阻尼系数分别以ρπRT2ω、ρπR2Tω和ρπR3T2ω进行无因次化。

图3和5分别为该气浮筒型基础的附加质量和辐射阻尼系数随着频率的变化在不同吃水下的变化规律，图4和6分别为该气浮筒型基础结构的垂荡水动力系数无因次化的数值计算结果。在级数计算中截取运算的前30项，计算结果表明，可以满足级数的收敛性。

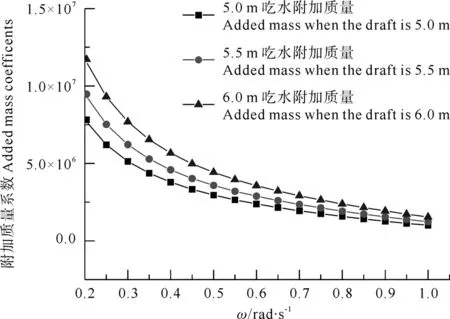
图3 不同吃水下垂荡附加质量

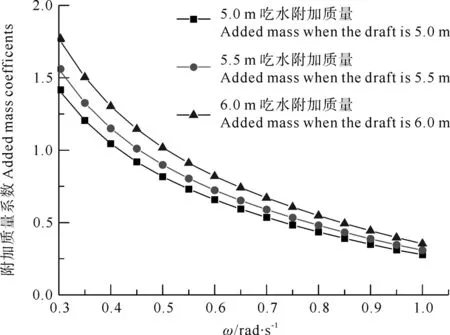
图4 不同吃水下无因次化垂荡附加质量

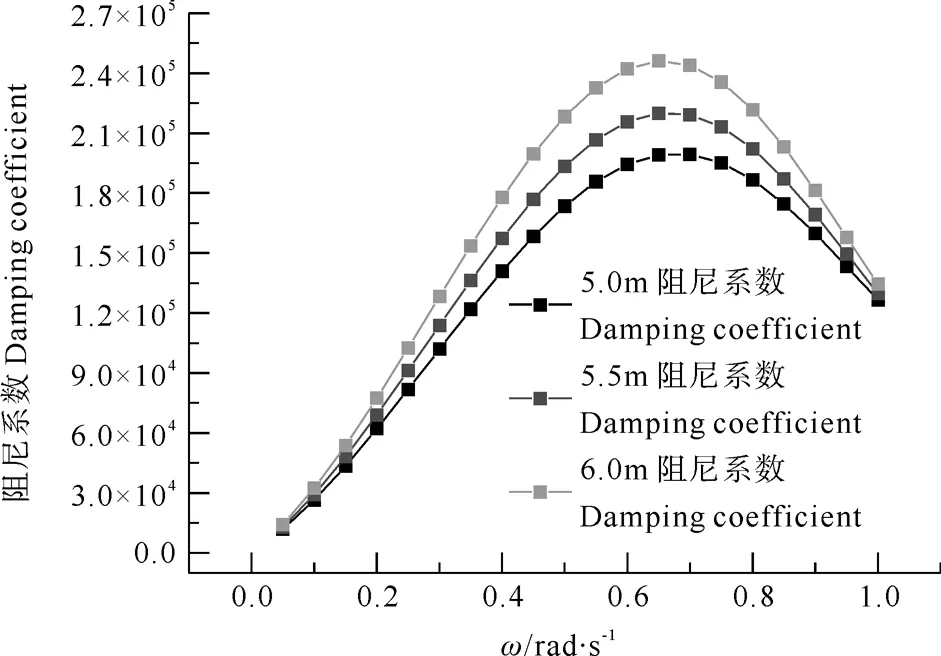
图5 不同吃水下垂荡阻尼系数

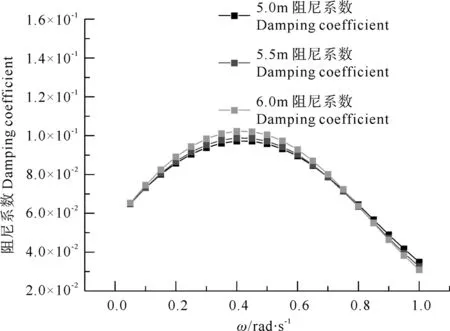
图6 无因次化垂荡阻尼系数

从图3和4可以看出，相同吃水下，随着入射波浪频率的变大，结构的附加质量呈不断下降的趋势，波浪频率越高，变化趋于平缓；在相同的入射波浪频率下，附加质量随着吃水的增大呈增大的趋势。从图5和6可以看出，相同的吃水下，结构的辐射阻尼系数随着波频的增加呈先增加后降低的趋势，且不同吃水相同的波浪频率下，辐射阻尼系数随吃水的增加而增加。

图7和8分别为不同水深下气浮筒型基础结构的垂荡附加质量和辐射阻尼的变化规律。从图中可以看出，在相同的水深下，垂荡运动的附加质量随着波浪频率的增加呈衰减的变化规律，但是辐射阻尼系数随着水深呈先增加后降低趋势，都会有“拐点”产生，也就是说，其辐射阻尼都有最大值；不同的水深下，筒型基础结构的附加质量随着水深的增加呈增大的趋势，且在波频低的增加幅度远远大于波频高的增加幅度，辐射阻尼系数随着水深的增加呈降低的趋势，且出现最大值“拐点”位置随水深的增加偏于波频低的范围。

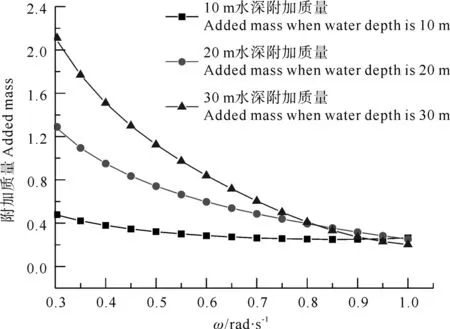
图7 不同水深下的无因次化垂荡附加质量

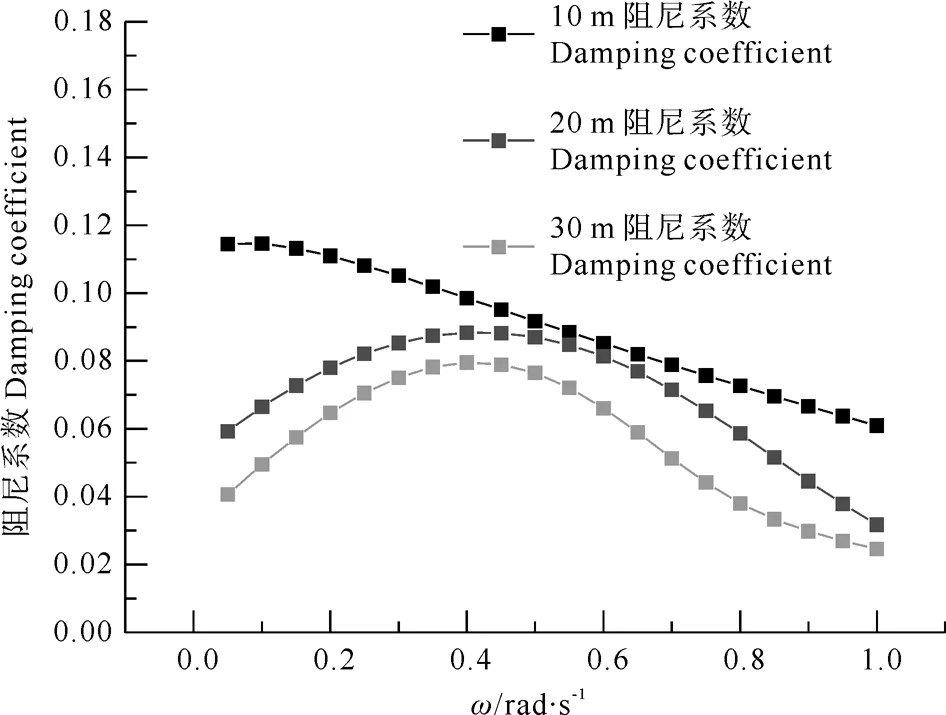
图8 不同水深下的无因次化垂荡辐射阻尼系数

4 结语

本文通过引入考虑气垫影响的无因次参数α处理筒内气水界面的非线性边界条件，基于三维势流理论采用半解析法的特征函数展开和匹配渐进法对气浮筒型基础结构的垂荡运动模式下的辐射问题进行求解，推导得到垂荡运动的速度势、附加质量以及辐射阻尼系数等水动力学参数，得到了气浮结构垂荡运动的一些规律，即筒内气垫的存在对结构垂荡具有较大的影响，在中国海浪的频率范围内，垂荡运动的附加质量随着频率的增大呈下降的趋势，附加阻尼在某一波浪频率范围内总能取得最大值，计算垂荡水动力参数时，必须考虑结构的内部因素和外界环境因素。

[1] 丁红岩, 郭卫波, 张浦阳， 等. 近海浅滩地区大尺度海上风电筒型基础在风荷载作用下的响应 [J]. 天津大学学报(自然科学与工程技术版), 2013, 46(2): 121-126.

[2]ZhangPuyang,DingHongyan,LeConghuan,etal.Towingcharacteristicsoflarge-scalecompositebucketfoundationforoffshorewindturbines[J].JournalofSoutheastUniversityEnglishEdition, 2013, 29(3): 300-304.

[3] 丁红岩, 翟少华, 张浦阳. 海上风电大尺度顶承式筒型基础承载力特性有限元分析 [J]. 工程力学, 2013, 30(6)： 124-132.

[4] 丁红岩, 于 瑞, 张浦阳，等. 海上风电大尺度预应力筒型基础结构预应力优化设计 [J]. 天津大学学报, 2012, 45(6): 473-480.

[5] 乐丛欢, 丁红岩, 张浦阳. 拖缆长度对筒基平台气浮拖航影响的试验研究 [J]. 哈尔滨工程大学学报, 2012, 33(7): 811-816.

[6] 丁红岩, 乐丛欢, 刘宪庆， 等. 四筒基平台拖航试验分析-水深影响研究 [J]. 天津大学学报, 2012, 45(2): 160-165.

[7] 丁红岩, 刘宪庆, 刁景华. 干舷高度影响筒型基础平台拖航试验研究 [J]. 船舶力学, 2012, 16(5): 490-496.

[8] 茅春浦.流体力学 [M].上海: 上海交大出版社, 1995.

[9]GarrettCJR.Waveforcesonacirculardock[J].JournalofFluidMechanics, 1971, 46: 129-139.

[10]YeungRW.Addedmassanddampingofaverticalcylinderinfinite-depthwater[J].AppliedOceanResearch, 1981, 3(3): 119-133.

[11]SabuncuT,CalisalS.Hydrodynamiccoefficientsforverticalcircularcylindersatfinitedepth[J].OceanEngineering, 1981 (8): 25-63.

[12]LandwebferL,ShahshahanA.Addedmassesandforcesontwobodiesapproachingcentralimpactinaninviscidfluid[J].JournalofShipResearch, 1992, 36(2): 99-122.

[13]ClarkeD.Calculationoftheaddedmassofcircularcylindersinshallowwater[J].OceanEngineering, 2001, 28(9): 1265-1294.

[14] 马烨, 单雪雄. 数值计算复杂外形物体附加质量的新方法 [J]. 计算机仿真, 2007, 24(5)： 395-398.

[15] 黄旋, 鲁传敬, 李杰. 带空泡运动航行体的附加质量研究 [J]. 水动力学研究与进展A辑, 2009, 24(6): 800-806.

[16] 王高峰， 筒型基础平台的自摇运动和拖航过程中的响应研究 [D]. 天津：天津大学， 2006.

[17]KimDS,IwataK.NonlinearInteractionofsecondorderStokeswavesandtwo-dimensionalsubmergedmooredfloatingstructure[J].InternationalJournalofOffshoreandPolarEngineering, 1994, 4(2): 88-96.

责任编辑 陈呈超

Study on Heaving Hydrodynamic Coefficient of Air-Floating Bucket Foundation

DING Hong-Yan1, 2, 3， SHI Jian-Chao3，ZHANG Pu-Yang1, 2, 3， LIU Xian-Qing3

(1. The State Key Laboratory of Hydraulic Engineering Simulation and Safety, Tianjin University, Tianjin 300072, China;2. The Key Laboratory of Coast Civil Structure Safety, Ministry of Education,Tianjin University,Tianjin 300072， China; 3.School of Civil Engineering, Tianjin University,Tianjin 300072,China)

Bucket foundation has been widely used in the exploitation of ocean resources as a new style foundation. Based on the background of the key technologies of air-cushion towing of the rapid construction of large-scale bucket foundation in offshore wind farms and the foundation type in exploitation of marginal oil fields，the motion responses of bucket foundation were studied in this paper. The nonlinear boundary conditions on the gas-water interface in the bucket are coped with by the introduction of the dimensionless parameterαconsidering the influence of air cushion，and based on the three-dimensional potential flow theory using the semi analytical method of Eigen function expansion and progressive matching method，the basic laws of heave were studied. Taking composite foundation CBF-3-150 of offshore wind turbine as a case，heaving hydrodynamic coefficient was solved by design a calculating program use programming platform MATLAB.

bucket foundation；air-floating structure；heave；hydrodynamic coefficients；nonlinear

国家自然科学基金项目(51309179)；天津应用基础与前沿技术研究计划项目(13JCYBJC19100；14JCQNJC07000)资助

2014-06-10；

2014-12-10

丁红岩(1963-)，男，教授，博导。E-mail:dhy_td@163.com

❋❋通讯作者： E-mail:zpy_td@163.com

P752

A

1672-5174(2015)12-113-06

10.16441/j.cnki.hdxb.20140182