黄土高原7百万年以来黄土古季风演变信号多尺度分析

张宝方, 冯秀丽, 林 霖, 肖 晓, 李 沛

(中国海洋大学 海洋地球科学学院， 山东 青岛 266100)



黄土高原7百万年以来黄土古季风演变信号多尺度分析

张宝方, 冯秀丽, 林 霖, 肖 晓, 李 沛

(中国海洋大学 海洋地球科学学院， 山东 青岛 266100)

本文在前人对黄土高原灵台剖面的研究基础上，以磁化率、平均粒径分别作东亚夏、冬季风替代指标，采用经验模态分解(Empirical Mode Decomposition, EMD)方法对其粒径、磁化率时序进行不同时间尺度周期的分离，以探讨7百万年来东亚冬、夏季风演化时频特征及其主要天文控制因子。结果表明，EMD方法可以灵敏地捕捉到东亚冬、夏季风“Milankovitch天文周期”(如～2万年、～4万年、～10万年等典型轨道周期)，特别是～40万年、～100万年等偏心率长周期，且与传统的Blackman-Tukey功率谱分析的结果基本吻合；天文长周期对东亚冬、夏季风的影响不可忽视。

黄土高原；粒度；磁化率；经验模态分解(EMD)；功率谱

黄土高原气候主要受东亚冬、夏季风影响，堆积的第三纪以来的黄土-古土壤沉积序列应该记录了同期大气环流系统的演化过程[1-3]，对其进行周期性分析特别是对天文长周期的捕捉有望对黄土高原冬、夏季风的演化特征获得更全面的认识，并可为研究东亚季风的控制因子和演化机制提供依据。

气候变化是一种非平稳和非线性的过程，前人多采用基于傅里叶变换的传统谱分析方法，在处理相关问题时存在其自身无法克服的缺陷[4-5]。经验模态分解EMD方法在理论上可以应用于任何类型的信号分解[6]，该方法能较好地解决资料时序的非线性和非平稳性问题，给出各信号分量的时频特征，并且能够在对长周期变化的分辨方面给出较高的精度[7]。

本文选取前人公开发表的黄土高原灵台剖面第四纪黄土磁化率、平均粒径时间序列数据[8]，以磁化率、平均粒径作东亚夏、冬季风替代指标[4,9-11]，采用经验模态分解EMD方法对其粒径、磁化率时序进行不同时间尺度周期的分离，以探讨第四纪及其以前东亚冬、夏季风演化时频特征及其主要天文控制因子。

1 研究方法

本文对时间序列的时-频域特征进行分析时采用的方法是EMD方法，其优点在于处理非线性、非平稳信号时更为有效，但也存在一定的缺陷[12-13]；对时间序列的频域特征采用的是功率谱分析中的Blackman-Tukey方法(BT法)，其优点在于不可能产生伪造的谱特征，弱点在于分辨率低，许多特征被显著平滑了[14-15]；因此文中将两种方法的结果进行相互对比、验证。

1.1功率谱分析

功率谱分析[16-18]是以傅里叶变换为基础的频域分析方法，其意义为将时间序列的总能量分解到不同频率上的分量，根据不同频率的波的方差贡献诊断出序列的主要周期，从而确定出周期的主要频率，即序列隐含的显著周期。其提取显著周期的简单计算流程见文献[16]。

1.2 EMD方法

EMD方法是近年发展起来的希尔伯特-黄变换(Hilbert-Huang Transform, HHT)的核心部分，其基本原理见文献[19-21]。它突破了传统的基于Fourier变换方法的局限，比小波法有更强的局部表现能力，所以在处理非线性、非平稳信号时更为有效[7,22-23]。

另外，在古气候记录中较长周期的分辨问题上，EMD方法较好地解决了资料时序的非平稳和非线性的问题，并且能在对长周期变化的分辨方面给出较高的精度[19]。实际资料时序短导致许多较长的天文周期无法检出是古气候时序资料周期分析中的常见困难[4]，如除20、40和100 ka等典型轨道周期之外，还存在400 ka、600 ka、1 Ma和2 Ma等更长的天文周期，由于受到地层时间跨度的限制而在一般的剖面中不易觉察。EMD方法的引入，使得考察400 ka天文周期，甚至上百万年等级的周期成为了可能。

EMD方法虽然表现出很多良好的特性，对于分析实际存在的非线性与非平稳性信号十分有效，但也存在一些问题[12-13]。针对端点“飞翼”问题，本文通过常数延拓(序列两端均延拓N/10的长度，N为序列长度)的方法先对信号端部进行适当延伸，然后再截取有效长度。结果表明，这种方法简单明了，可以较有效地抑制端点效应。

2 结果

为了提高对不同周期进行提取的分辨率，本文对粒度时序(见图1)和磁化率时序(见图2)按照不同的时间跨度进行了功率谱分析和EMD分解。

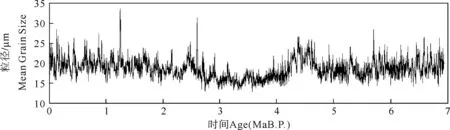
图1 粒度时间序列(7 Ma B.P.至今)

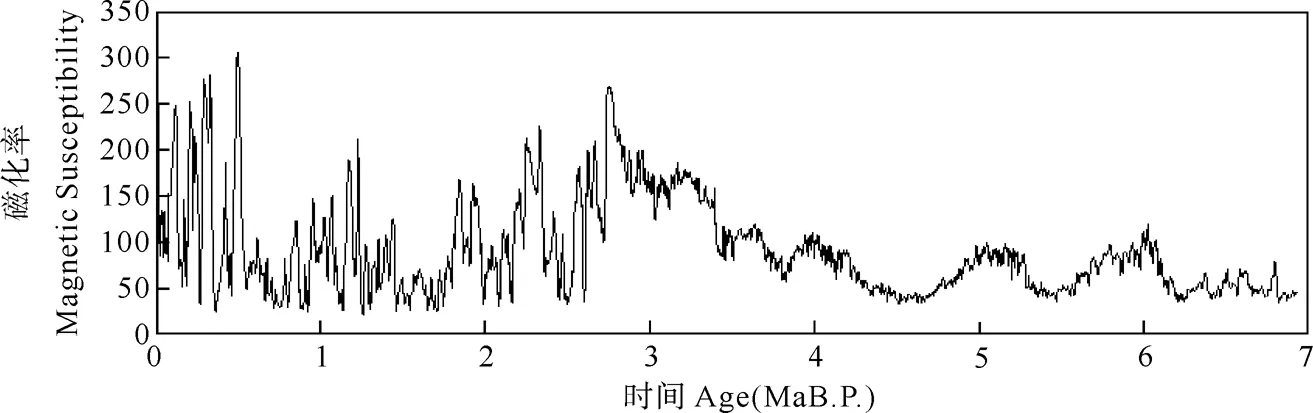
图2 磁化率时间序列(7 Ma B.P.至今)

2.1 1 Ma B.P.至今

按照不同的步长(0.5和1 ka)对粒度、磁化率时序分别进行3次样条插值后做功率谱分析，检出的大于90%置信度的周期主要有～100 ka、～41.7 ka、～22.7 ka、～11.6 ka等(见图3)。

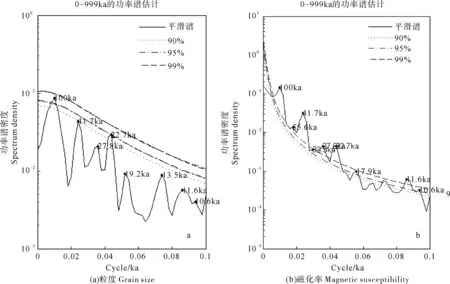
图3 插值步长1 ka，m=250的粒度、磁化率时序功率谱分析结果

通过EMD获得的每一个IMF分量都有不同的振幅和频率，分析得出，这些分量大多具有物理意义(见图4)。

粒度时序，IMF1和IMF2对应～7.6 ka和～13 ka岁差周期的拍频周期；IMF3和IMF4对应31和50 ka地轴倾斜波动；IMF5对应～100 ka偏心率短周期的波动；磁化率时序，IMF1对应～10.5 ka和～13.9 ka岁差周期的拍频周期，IMF2对应～21.3 ka岁差周期，IMF3大致对应～41 ka地轴倾斜周期，IMF4表示～90.8 ka偏心率短周期。

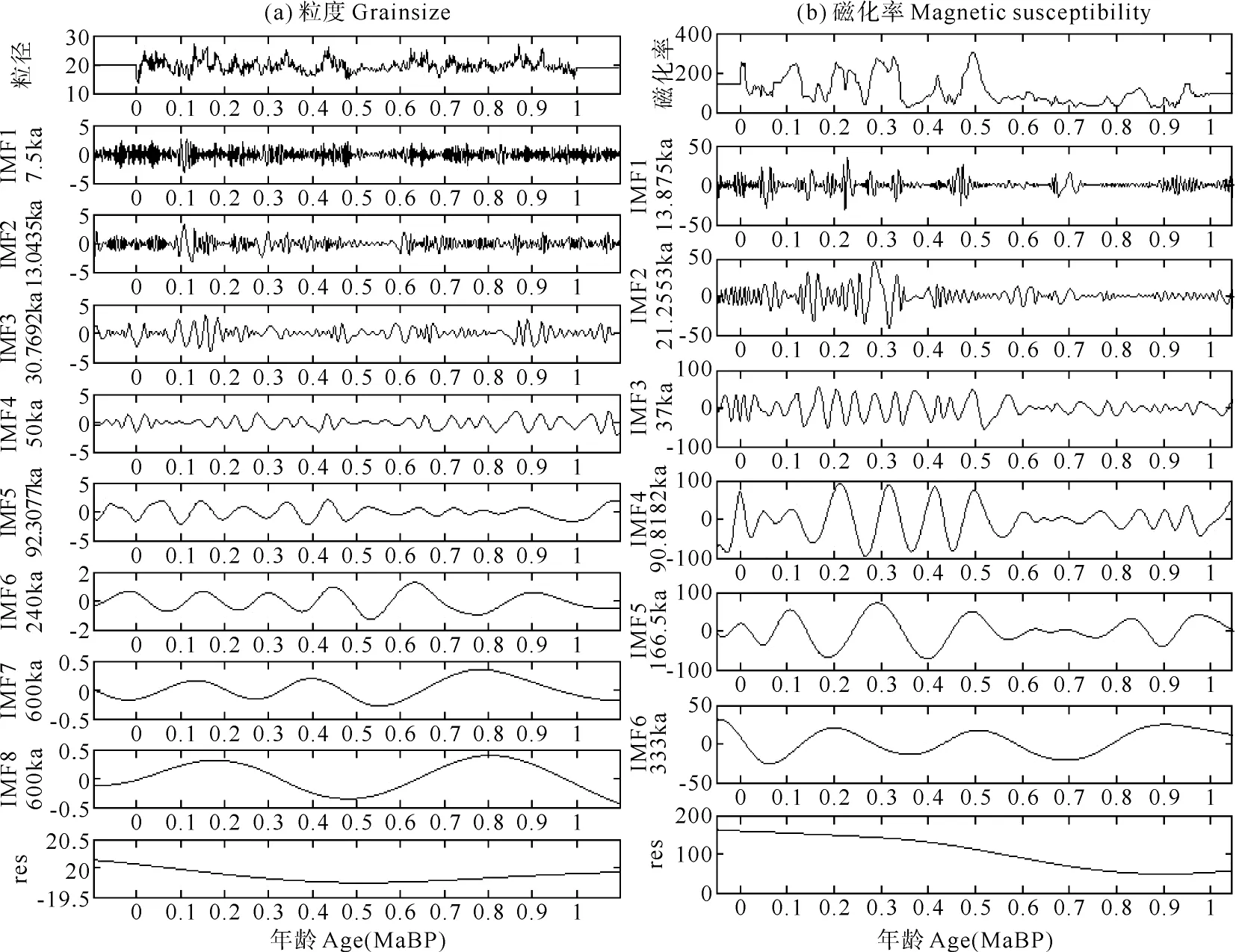
图4 1 MaB.P.至今的粒度、磁化率时序EMD分解结果

2.2 2.6 Ma B.P.至今

按照不同的步长(1和2 ka)对粒度、磁化率时序分别进行3次样条插值后做功率谱分析，检出的大于80%置信度的周期主要为～400 ka、～100 ka、～41 ka、～23.5 ka(～23.2 ka)(图5,6)，另有～19 ka、～13.3 ka、～10.8 ka、～7.5 ka等短周期未于图中显示。

粒度时序，IMF2对应～11.6 ka岁差周期的拍频周期，IMF3对应～20.1 ka岁差周期，IMF4表示～42.0 ka地轴倾斜周期，IMF7对应～433 ka偏心率长周期的波动；磁化率时序，IMF1对应～10.5 ka岁差周期的拍频周期，IMF2对应～19.9 ka和～21.5 ka岁差周期，IMF4对应～93 ka偏心率短周期，IMF6对应～348 ka偏心率长周期(见图7)。

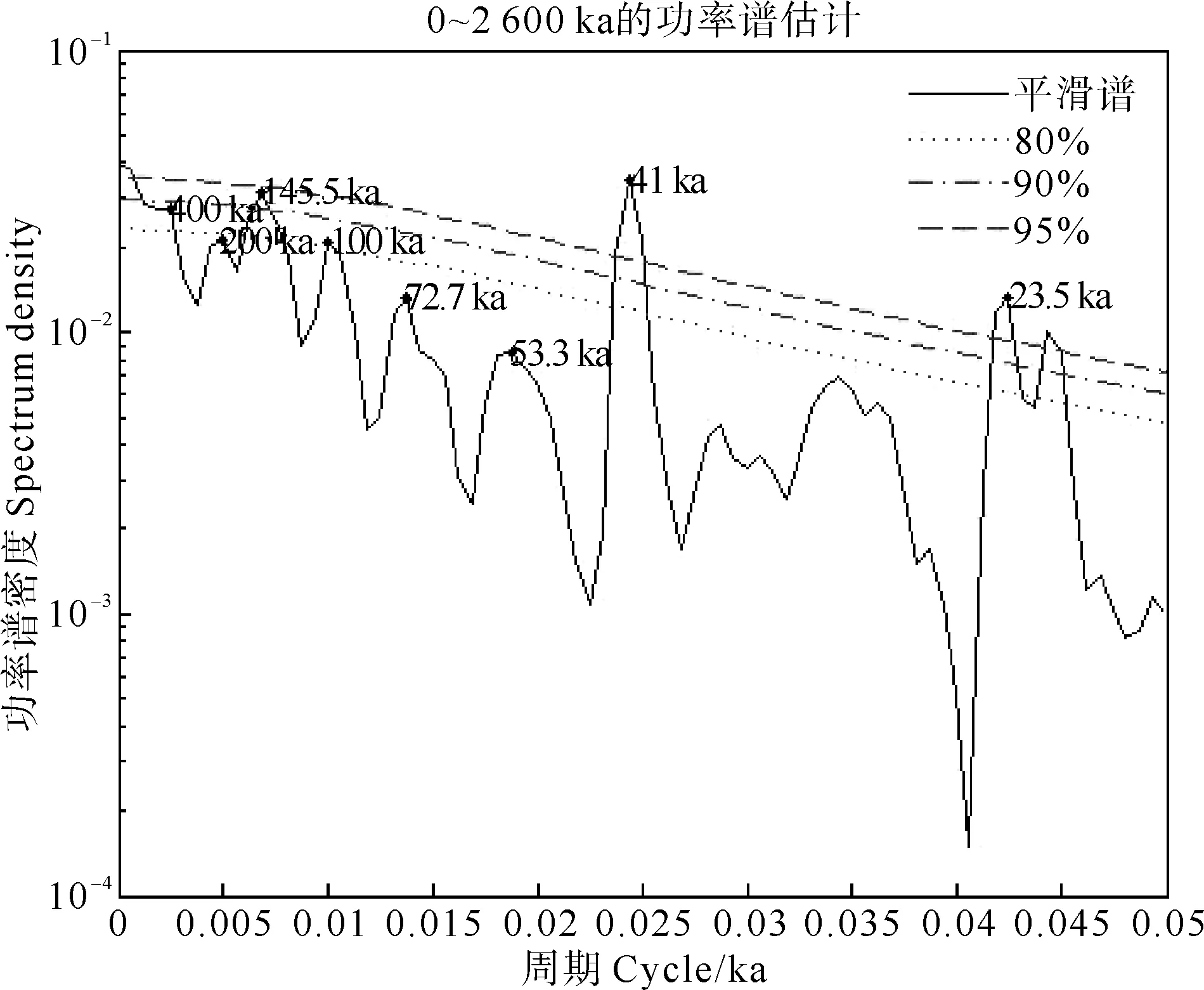
图5 插值步长2 ka，m=400的粒径时序功率谱分析结果

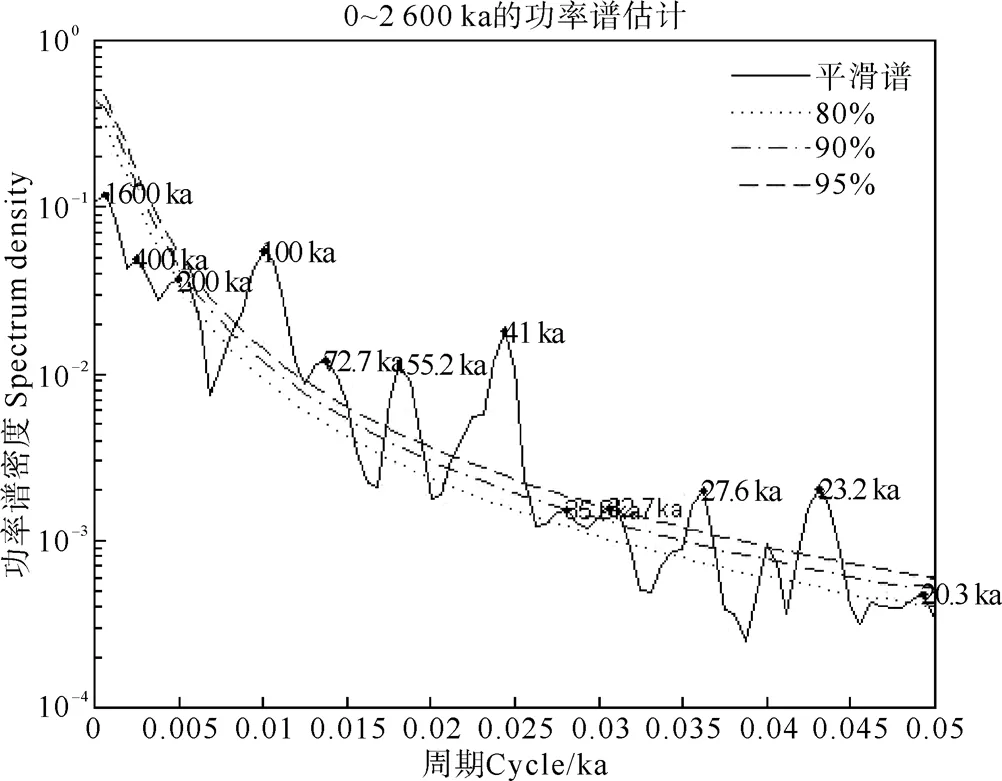
图6 插值步长2 ka，m=400的磁化率时序功率谱分析结果

2.3 7MaB.P.至今

按照不同的步长(2ka、5ka、10ka)对粒度、磁化率时序分别进行3次样条插值后做功率谱分析，检出的大于80%置信度的周期为～1Ma、～100ka、～40.8ka、～23.7ka(见图8，9)，另有～19ka、～12.1ka、～7.2ka等较短的周期未于图中显示。～400ka、～200ka等周期虽检出，但是置信度较低，可能是周期特征不够明显，因而被较短或较长的周期所掩盖。

粒度时序，IMF1对应～10.4ka岁差周期的拍频周期，IMF2对应～43.1ka地轴倾斜周期，IMF4表示～100ka偏心率短周期，IMF5-IMF6大致对应～400ka偏心率长周期，IMF7对应～1Ma的周期波动；磁化率时序，小周期的分辨率较低，但很好地提取了～1Ma这一长周期(IMF6)(见图10)。

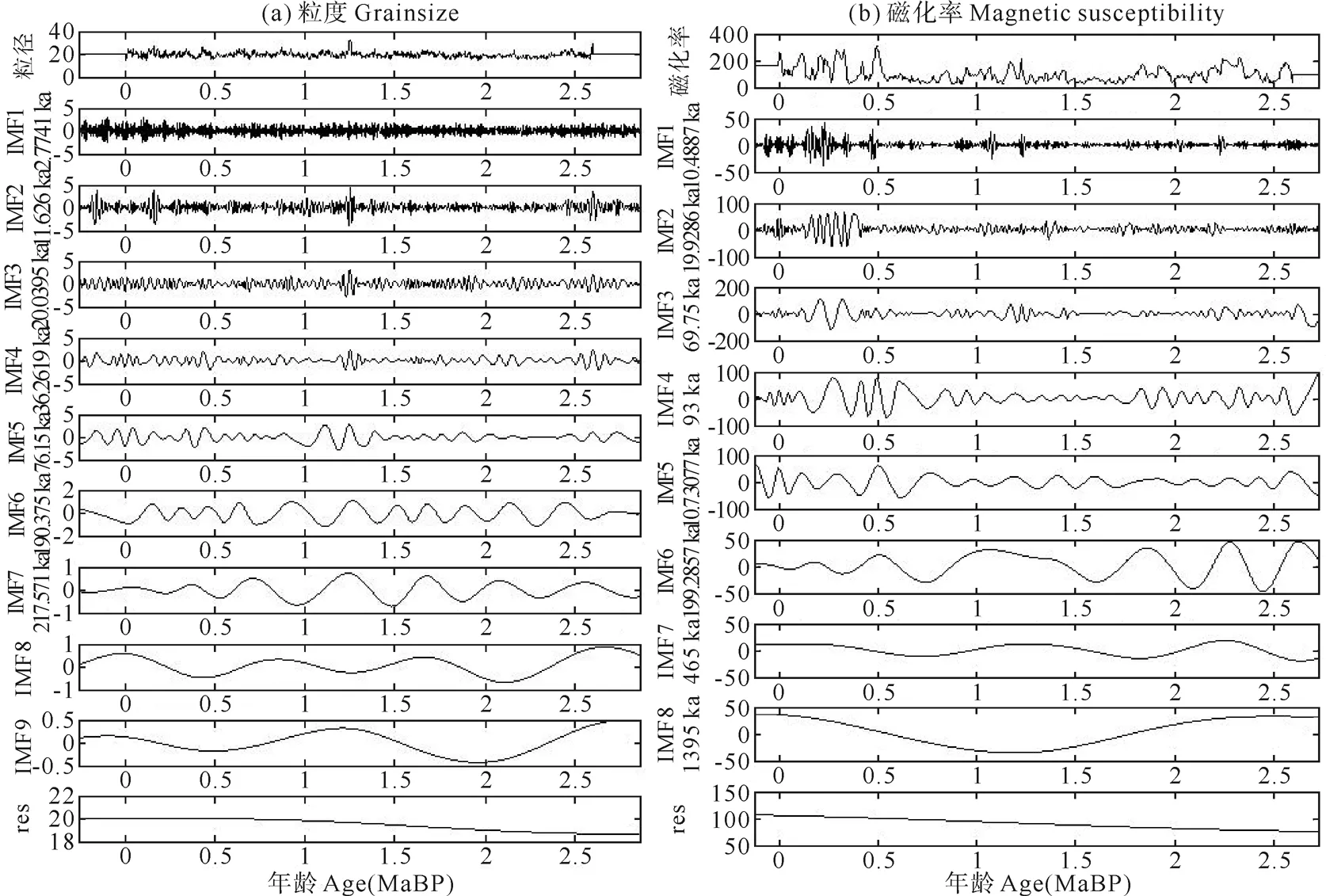
图7 2.6 MaB.P.至今的粒度、磁化率时序EMD分解结果

3 讨论

通过综合对比、分析，对粒径、磁化率时序进行功率谱分析和EMD分解能够分别得到不同时间尺度的周期，可以看出二者的结果能够互相印证，EMD方法对米兰科维奇理论周期(特别是～1Ma长周期)的提取效果较好。

3.1 冬、夏季风不同时间尺度周期特征

3.1.1 岁差及其拍频周期 两种方法检出的～7.6、～10.5、～11.8、～20.8、～23.8ka等周期对应岁差周期理论值23ka、半岁差11.5ka和1/3岁差7.6ka等[24]，半岁差周期在受到东亚夏季风强烈影响的南中国海[25-26]、印度季风影响下的印度洋[27]、非洲季风影响下的东地中海地区[28]的海洋沉积中和东南季风影响下的中国黄土高原风尘沉积[29]中都有发现，综合来看，半岁差周期实际表现为9～15ka的周期。

3.1.2 地轴倾斜周期 同时，EMD方法检出的地轴倾斜的周期分别为～40ka、～42ka、～40.8ka，对应于功率谱分析的～41.7、～41、～40.8 ka，并且与理论值41 ka相吻合[24]。这主要是由于地球自转轨道与地球公转轨道面之间倾角的变化，导致太阳辐射的变化而产生的。地球轨道面在空间上的变动，致使地球的自转相对于地球的轨道面的夹角在22°-24°30′之间变化，从而黄赤交角产生了40 ka周期变化。黄赤夹角每增加1°，极地的年辐射量增加4.02%，赤道减少0.35%，使得行星季风带向北移动，因而地球轨道面的变化对地质时期东亚季风气候影响十分显著，导致了大陆上植被与大气降水时间尺度为40 ka左右的变化[30]。

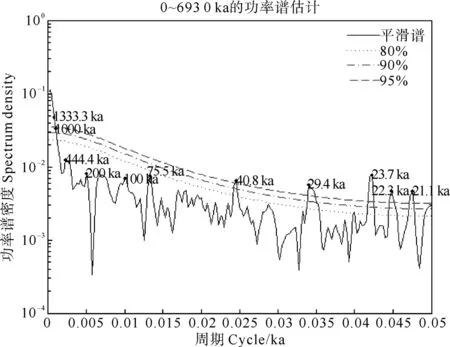
图8 插值步长10 ka，m=200的粒度时序功率谱分析结果

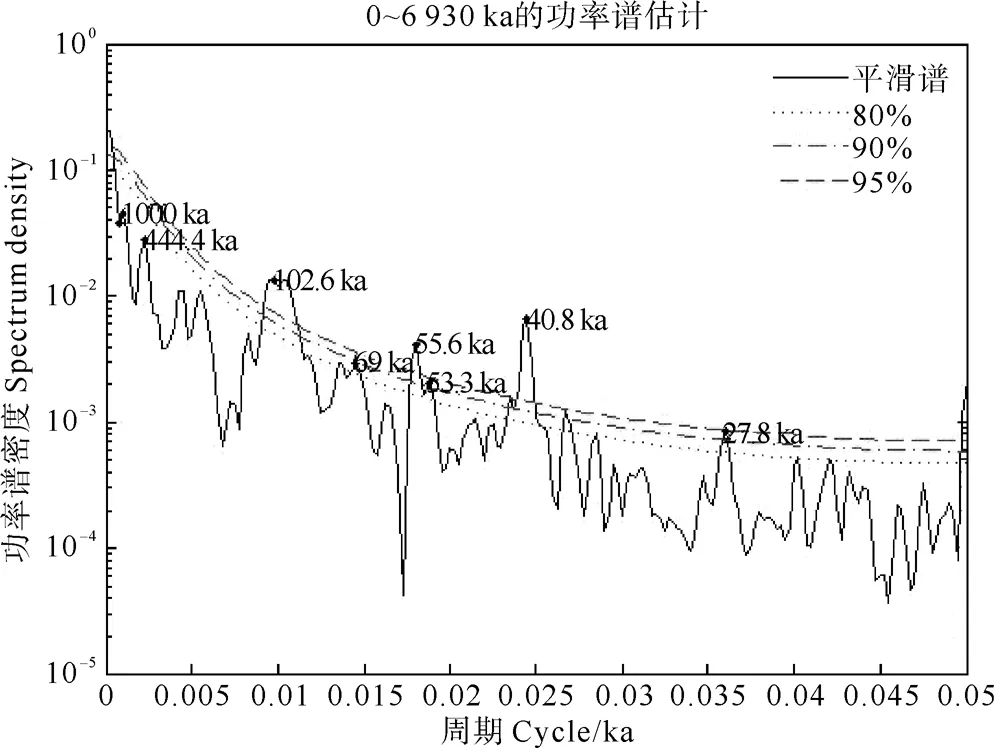
图9 插值步长10 ka，m=200的磁化率时序功率谱分析结果

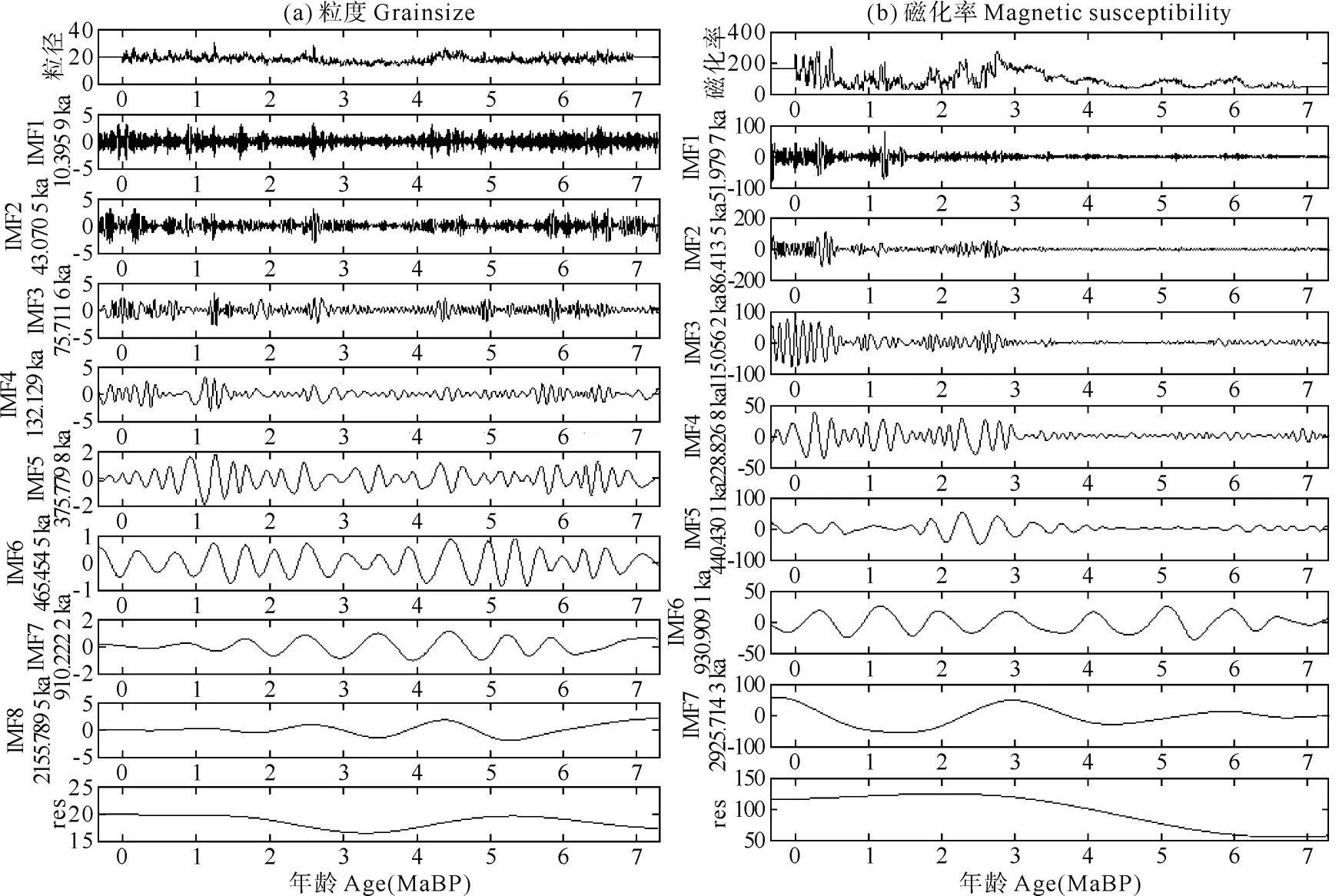
图10 7 MaB.P.至今粒度、磁化率时序的EMD分解结果

3.1.3 偏心率周期 对于偏心率周期，两种方法在粒度、磁化率时序中均有检出，而其产生的原因仍是古气候学界面临的问题，因为地球轨道偏心率引起太阳辐射量的变化太小，不足以视为100 ka周期冰期旋回的直接驱动力[31]。余志伟等[29]用非线性机制如100 ka周期与岁差、半岁差周期非线性耦合加以解释，也有解释将其归因于北半球冰盖动力学[32]，而北半球冰量变化是东亚冬季风变化的主要驱动力[33]。黄土磁化率作为东亚夏季风变化的指标，可能更多地受到来自低纬海洋的影响，因此能够记录到同海洋沉积物相一致的气候变化周期。

3.1.4 其他长周期 检出的～400 ka偏心率长周期和～1 Ma的天文长周期已在海洋地质等长记录中捕捉到[34]，而黄土记录中相关研究较少，所以本文的尝试具有一定意义。

3.1.5 小结 除从粒度、磁化率时序中分离出了岁差～23 ka、地轴倾斜～41 ka、偏心率～100 ka等典型轨道周期模态外，还在岁差模态中检出了～11.4 ka、～7.5 ka的拍频周期，说明东亚冬、夏季风的演化明显受外部天文因素——偏心率、斜率、岁差等轨道参数的驱动；检出的偏心率长周期，暗示了天文长周期对东亚冬、夏季风的影响不可忽视，其具体成因还有待进一步研究；～400 ka、～100 ka周期、岁差、半岁差及三分之一岁差的集中出现，指示了东亚季风系统对太阳辐射的非线性响应，而且东亚夏季风系统具有热带特征[35]。

3.2 EMD的优势

到目前为止，在Milankovitch周期的研究中，建立在傅立叶变换的基础上的频谱分析是最主要的方法之一，它可以在频率域内获得非常高的分辨率，因此被广泛应用于各种古气候记录体系，但无法同时表现这些不同的周期成分在时间域的变化。而对于古气候研究而言，了解不同周期成分随时间变化的过程是非常重要的，它能够提供关于古气候系统的动态演化信息。

EMD方法是依据原始信号本身的固有特性进行分解的，无须预先设定任何基函数。经EMD分解得到的IMF序列是直接从原始数据中分离出来的，事先无需确定分解阶次，不受人为因素影响，不存在机械分解，因此，IMF序列能更好地反映原始信号的固有物理特性[36]，以EMD方法为基础对其进行研究应该更切合实际。

谱分析能够检出的周期长度有赖于地质记录的时间跨度，由本文所获得的周期长度可以看出，EMD能够使这种依赖性大大降低，最大甚至能获得约1/3时间跨度的长周期，这一优势是传统谱分析方法无法比拟的，而且EMD方法能够在对长周期变化的分辨方面给出较高的精度[7]。

4 结论

本论文通过对前人黄土高原灵台剖面黄土-古土壤沉积古气候代用指标时间序列的定量研究，取得以下认识：

(1)粒径、磁化率时间序列的功率谱分析、EMD分解检出典型的轨道周期和岁差拍频周期，说明黄土高原冬季风的演变明显受米兰科维奇理论的天文因素影响。

(2)用EMD方法灵敏地捕捉到不同时间尺度周期在不同时段的演变过程，实现了对长周期的高精度分辨，大大降低了检测周期长度对地质记录时间跨度的依赖，获得了以往用传统谱分析方法无法提取的信息。本文对中国黄土古气候变化时间序列信号进行深度分析是有效的。

(3)～40万年、～100万年等天文长周期对东亚冬季风的影响不可忽视，有待于进一步研究。

(4)采用EMD方法提取周期成分，虽然相对传统方法来说具有优势，但其检出的长周期的可靠性还有待进一步验证。相信随着EMD方法的不断完善，它在古气候演变研究中将有更广的应用前景。

[1] 刘东生.黄土与环境 [M].北京:科学出版社, 1985：191-208.

[2] An Z S, Liu T S, Lu Y， et al. The long-term paleomonsoon variation recorded by the loess-paleosol sequence in central China [J]. Quaternary International, 1990, 7/8: 91-95.

[3] An Z S. The history and variability of the East Asian monsoon [J].Quaternary Science Reviews, 2000, 19: 171-187.

[4] 刘冬雁. 川西高原甘孜黄土记录的早更新世晚期以来的古气候变化 [D]. 青岛: 中国海洋大学海洋, 2009.

[5] 刘冬雁, 李巍然, 乔彦松, 等. 基于EMD分解的甘孜黄土磁化率记录的西南季风演化周期性 [J]. 地球科学(中国地质大学学报), 2010, 35(4): 533-541.

[6] 林振山, 汪曙光. 近四百年北半球气温变化的分析: EMD方法的应用 [J]. 热带气象学报, 2004, 20(1): 90-96.

[7] 王卫强, 陈宗镛, 左军成. 经验模态法在中国沿岸海平面变化中的应用研究 [J]. 海洋学报, 1999, 21(6): 102-109.

[8] Sun, Y B, An Z S, Clemens S C, Bloemendal J, Vandenberghe J. Seven million years of wind and precipitation variability on the Chinese Loess Plateau [J]. Earth and Planetary Science Letters, 2010， 297: 525-535.

[9] 安芷生, Porter S C, Kukla G. 最近13万年黄土高原季风变迁的磁化率证据 [J]. 科学通报, 1990, 35(7): 529-532.

[10] 孙东怀. 晚新生代黄土高原风尘序列的磁性地层与古气候记录[D]. 北京： 中国科学院研究生院(地球环境研究所)， 1997.

[11] 熊尚发, 刘东生, 丁仲礼. 两个冰期-间冰期旋回的黄土记录及其古气候意义[J]. 地理科学. 2002(1): 18-23.

[12] 王伟. Hilbert-Huang变换及其在非平稳信号分析中的应用研究 [D]. 北京： 华北电力大学， 2008.

[13] 黄大吉, 赵进平, 苏纪兰. 希尔伯特-黄变换的端点延拓[J]. 海洋学报(中文版)， 2003(1)： 1-11.

[14] 魏建晶, 郭正堂. 900 ka以来黄土-古土壤序列记录的风尘铁含量变化及其古气候意义 [J]. 科学通报, 2003, 48(11): 1214-1218.

[15] Blackman R B, Tukey J W. The Measurement of Power Spectra [M]. NewYork: Dover, 1958.

[16] 魏凤英. 现代气候统计诊断与预测技术 [M]. 第2版. 北京: 气象出版社, 2007: 77-82.

[17] 黄嘉佑, 李黄编著. 气象中的谱分析 [M]. 北京: 气象出版社, 1984: 13-45.

[18] 李平, 卢文喜, 辛欣, 等. 挠力河流域降水量序列的功率谱分析和最大熵谱分析[J]. 世界地质, 2008(1): 63-67.

[19] 王婷. EMD算法研究及其在信号去噪中的应用 [D]. 哈尔滨工程大学, 2010.

[20] 郭东亮, 戴宪华, 张铁军. 基于自相关周期估计的EMD端点延拓方法[J]. 数据采集与处理, 2010(6): 712-715.

[21] Huang N E, Shen Z, Long S R, et al. The empirical mode decomposition and the Hilbert spectrum for non-linear and non stationary time series analysis [J]. Proceeding of the Royal Society of London A,1998, 454: 903-995.

[22] 李强, 吴健, 许正文, 等. 利用EMD方法提取太阳活动周期成分 [J]. 空间科学学报, 2007, 27(1): 1-6.

[23] 熊学军, 郭炳火, 胡筱敏, 等. EMD方法和Hilbert谱分析法的应用与探讨[J]. 黄渤海海洋, 2002(2): 12-21.

[24] Berger A L. Support for the Astronomical Theory of Climatic Change [J]. Nature, 1977, 269: 44-45.

[25] 田军, 汪品先, 成鑫荣. 更新世南海南部上层海水结构变化的岁差驱动[J]. 自然科学进展, 2004, 14(6): 683-688.

[26] 陈国成, 郑洪波, 李建如, 等. 南海西部陆源沉积粒度组成的控制动力及其反映的东亚季风演化[J]. 科学通报, 2008, 52(23): 2768-2776.

[27] 刘海生, 方念乔, 艾星涛, 等. 深海碳酸盐岩心天然热释光变化特征[J]. 海洋学报, 2005, 27(1): 78-83.

[28] 黄恩清, 田军. 早上新世非洲季风与地中海表层生产力变化的岁差节律[J]. 地球科学(中国地质大学学报), 2007(3): 313-321.

[29] 余志伟, 丁仲礼. 黄土古气候记录中100 ka周期与岁差, 半岁差周期的非线性耦合关系[J]. 中国科学(D辑), 2003, 33(6): 520-528.

[30] 薛根元, 周锁铨, 陈旸, 等. 黄土高原260万年以来东亚夏季风演变信号研究[J]. 气候与环境研究, 2007, 12(1): 63-73.

[31] Shackleton N J. The 100 000-year ice-age cycle identified and found to lag temperature, carbon dioxide and orbital Eccentricity [J]. Science, 2000, 289: 1897-1902.

[32] Clark P U, Alley R B, Pollard D. Northern Hemisphere ice-sheet influences on global climate change[J]. Science, 1999, 286(5442): 1104-1111.

[33] Ding Z, Liu T, Rutter N W, et al. Ice-volume forcing of East Asian winter monsoon variations in the past 800,000 years[J]. Quaternary Research, 1995, 44(2): 149-159.

[34] Kashiwaya K, Ochiai S, Sakai H, et al. Orbit-related long-term climate cycles revealed in a 12-Myr continental record from Lake Baikal[J]. Nature, 2001, 410(6824): 71-74.

[35] 田军, 汪品先. 深海记录中的热带过程及其周期性 [J]. 地球科学-中国地质大学学报, 2006, 31(6): 747-753

[36] 王祝文, 刘菁华, 聂春燕. 基于 Hilbert-Huang 变换的阵列声波测井信号时频分析[J]. 地球科学(中国地质大学学报), 2008, 33(3): 387-392.

责任编辑 徐 环

Multi-Scale Analysis of the Paleomonsoon Evolution Signals in the Loess Plateau during the Last 7 MaB.P.

ZHANG Bao-Fang， FENG Xiu-Li， LIN Lin， XIAO Xiao， LI Pei

(College of Marine Geosciences, Ocean University of China, Qingdao 266100, China)

This thesis is based on previous studies and data of Lingtai profile in the Loess Plateau, regarding mean grain size and magnetic susceptibility as the proxy of the summer and winter monsoon. The method of Empirical Mode Decomposition(EMD) is applied, in order to separate the grain size sequence and magnetic susceptibility sequence in different cycle and investigate the evolution characteristics of east Asian paleomonsoon and its astronomical control factor during the Last 7 MaB.P. The results show that the EMD method can get the time domain features of the East Asian paleomonsoon “Milankovitch cycle” acutely, especially the long-term period of ～400 ka and ～1 Ma. The same conclusions are drawn from the power spectrum analysis results. The long-term “Milankovitch cycle” played an important role in the East Asian paleomonsoon evolution.

the Loess Plateau； mean grain size； magnetic susceptibility； empirical mode decomposition (EMD)； power spectrum analysis

2014-09-22；

2014-12-26

张宝方(1992-)，女，硕士生。 E-mail：13075381961@126.com

P512.2

A

1672-5174(2015)12-087-07

10.16441/j.cnki.hdxb.20140313