单轴自旋平面对固定平面的旋转角系数研究

张旭升，郭 亮，黄 勇，刘春龙

(中国科学院 长春光学精密机械与物理研究所，吉林 长春 130033)

0 引言

20 世纪20 年代，表面辐射换热领域提出了用于表征几何形状、大小及其相对位置的物理概念—角系数［1］，并被广泛应用于高温炉内换热［2－3］、航天器热控系统设计［4］、辐射采暖及散热［5－6］等诸多方面，在后续发展中衍生出辐射传递因子等类似概念。作为表面辐射换热领域的重要概念，国内外学者已对角系数进行了相关研究。张涛等［7］提出了计算角系数的能束均匀分步法，与有限元法结合后可用于求解复杂结构的角系数。王天鹏等［8］建立了计算角系数的高精度有限体积模型，并将其应用于计算地面建筑结构的辐射换热中。高亚峰等［9］采用等分圆弧射线扫描法实现了复杂建筑群内地面对天空角系数的快速简化求解。张伟清等［4］提出了基于角系数计算漫反射表面辐射传递因子的新方法，且计算误差主要源于角系数。M． R． Vuji i 等［10］采用蒙特卡洛法计算了平行矩形平面及各网格单元间的角系数，指出复杂结构辐射换热计算中，过分细化网格必将造成角系数计算误差的增大。同样，M．Mirhosseini 等［11］也采用蒙特卡洛法计算了圆柱面与相切矩形微元面间的角系数，文中着重分析了网格离散方案和单元光线数对计算精度和计算效率的影响。J．M． Cabeza －Lainez 等［12］应用几何光学原理推导了球冠面、圆锥面、椭圆面、抛物面等二次曲面间的角系数计算式。A． Bahadori 等［13］发展了一种计算矩形平面与微元面间角系数的简化方法，所得公式可用于快速解决工程领域的辐射换热问题。

综上所述，各文献的研究重点均集中在固定平面角系数计算或复杂结构角系数计算简化等方面，并未对转动部件角系数的高精度计算进行相关研究。鉴于此，本文将采用计算精度高、物理概念清晰、对复杂结构适应性强［6，14］的蒙特卡洛法建立单轴自旋平面对固定平面的旋转角系数计算模型。通过与典型自旋平面位置下解析式计算值的比对，验证物理模型及算法的正确性。在此基础上，分析旋转角度、初始相对位置等因素对角系数大小的影响，探讨发射光线数目和初始相对位置与统计标准差的关联性。

1 计算模型及验证

1．1 计算模型

角系数是用于表征物体表面结构特性对辐射换热影响程度的无量纲因子，计算时需满足以下限制条件:

(1)表面具有漫射特性且不透明;

(2)表面辐射热流密度在空间均匀分布［11，14］。

在上述条件下，建立了旋转角系数的物理模型及系统坐标系，如图1 所示。初始时刻，长L ×宽W的两矩形平面平行且中心正对，垂直距离为H。然后，单轴自旋平面沿着y 轴旋转，旋转方向与y 轴遵循左手螺旋定则，且90°为旋转角度的极限位置，如图1 中虚线框所示。

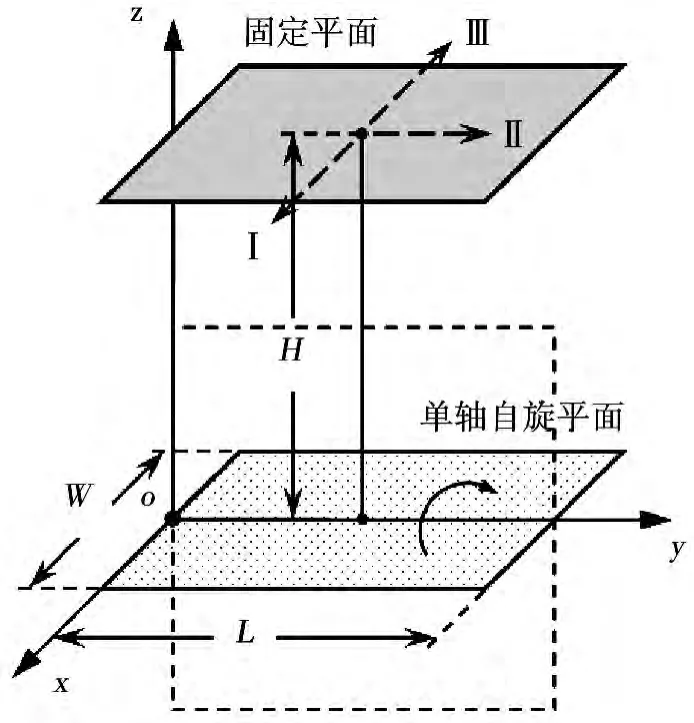
图1 旋转角系数物理模型及系统坐标系

在系统坐标系下，单轴自旋平面光线发射位置概率模型计算式如下

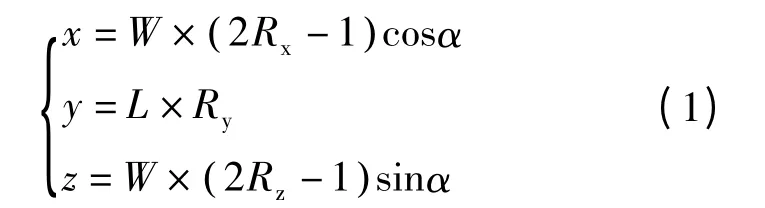
式中 α——单轴自旋平面旋转角/°;

Rx、Ry——［0，1］区间内独立均布随机数。

由于光线发射点位于单轴自旋平面上，故每次循环中满足关系式Rx=Rz。

对于漫发射单轴自旋平面，光线发射方向概率模型计算式如下

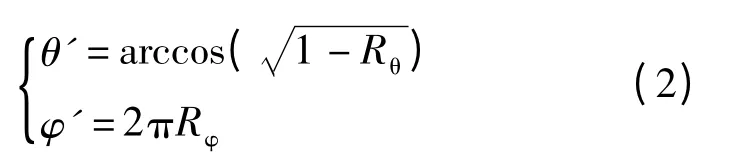
式中 θ'、φ'——自旋平面局部坐标系下发射光线

的天顶角和圆周角/°;

Rθ、Rφ——［0，1］区间内独立均布随机数。根据坐标变换关系可推导出如下角度变换关系式

再结合式(2)和反三角函数关系，即可求得系统坐标系下发射光线的天顶角θ 和圆周角φ。至此，已具备蒙特卡洛法计算旋转角系数的定解条件。为了便于对旋转角系数的分析讨论，规定L =W =H，均取无量纲单位长度1．0。

1．2 模型验证

为了验证旋转角系数物理模型及算法的正确性，将典型自旋平面位置下角系数与J．R．Howell 解析式计算值［15］进行比对，如表1 所示。其中，本文蒙特卡洛法计算中采用单次循环、发射光线数目为1．0 ×108根。此时，角系数计算值与发射光线数目已呈现无关性。

表1 典型自旋平面位置下角系数计算值

分析上表可知，无论自旋平面处于平行或垂直的典型位置下，本文角系数计算值均与文献［15］解析值大体一致，仅仅在小数点后5 位及以上存在微小差异，这也是基于概率统计的蒙特卡洛法所必然产生的随机误差［16］。

2 分析与讨论

2．1 平移矢量

为了分析旋转角度、初始相对位置等因素对角系数大小的影响，文中将固定平面沿矢量s 进行平移。依据平面中心点及边缘的相对位置关系，规划出0．25、0．5、0．75 和1．0 等4 种平移距离和3 种平移方向，并将平移距离为0．0 的情况定义为基准，据此所构造算例的具体内容见表2，角度β 为平移矢量s 的方位角。

表2 算例中固定平面的平移矢量

在各算例的模拟计算中，发射光线数目均取1.0 ×107根且为单次循环。角系数计算值如图2、图3、图4 所示，图中Δ(+x)=0．5 表示固定平面沿+x 方向平移0．5 个距离，其他以此类推。

图2 算例Ⅰ条件下的角系数计算值

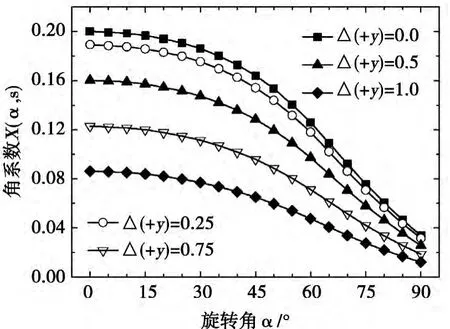
图3 算例Ⅱ条件下的角系数计算值

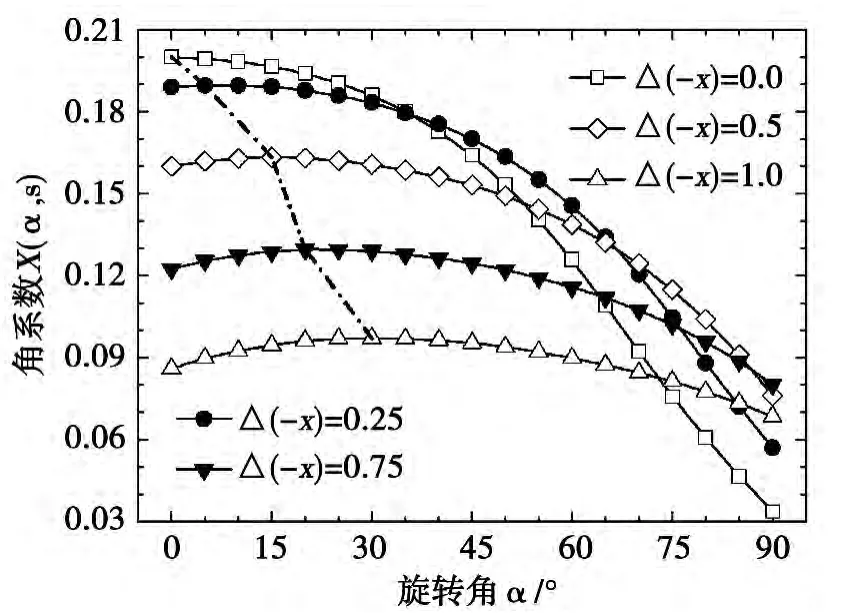
图4 算例Ⅲ条件下的角系数计算值

分析基准算例可知，随着旋转角的增大，角系数X (α，s)约从0．200 单调递减至0．034，且在旋转角大于45°后角系数呈线性下降趋势。图2 中给出固定平面沿+x 方向移动时旋转角度和初始位置对角系数的影响，即算例Ⅰ。随着平移距离Δ(+x)的增大，角系数变化范围逐渐减小，相同旋转角度对应的角系数明显下降;当Δ(+x)≥0．5 时，大角度角系数出现“零值现象”，该现象也从侧面验证了本文物理模型及算法的正确性。图3 中给出固定平面沿+y 方向移动时旋转角度和初始位置对角系数的影响，即算例Ⅱ。随着平移距离Δ(+y)的增大，角系数变化范围亦逐渐减小，但未出现“零值现象”;数据归一化后发现，不同Δ(+y)的角系数变化趋势与基准算例大体一致、差异微小。图4 中给出固定平面沿－x 方向移动时旋转角度和初始位置对角系数的影响，即算例Ⅲ。随着平移距离Δ(－x)的增大，角系数变化范围显著减小，当Δ(－x)=1．0 时，角系数仅分布在0．068 ～0．097 之间;而当Δ(－x)≠0．0 时，存在非零旋转角αmax使得角系数取得极大值，且Δ(－ x)与αmax呈正相关，如图4 点划线所示。

2．2 统计标准差

在蒙特卡洛法中，伪随机数程序性能优劣将直接关系到计算结果的精度［16］。为保证旋转角系数在允许误差范围内，文中将对不同旋转角和初始相对位置下的统计标准差进行分析。定义旋转角为α时，旋转角系数的统计标准差σ(α，k)计算式如下

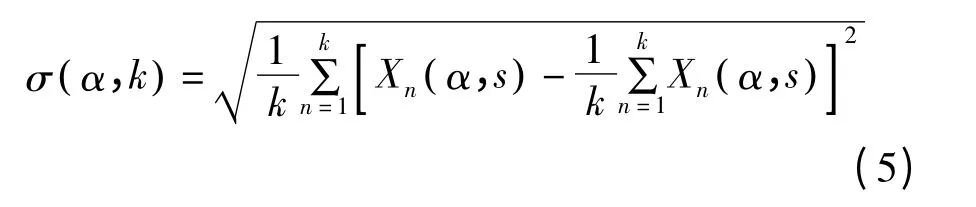
式中

k——蒙特卡洛法中旋转角系数的统计循环次数;

Xn(α，s) ——第n 次循环中旋转角为α 时的角系数。在统计标准差分析计算中，循环次数均为10 次。

图5 基准算例标准差与发射光线数目关系

图5 给出发射光线数目分别为1．0 ×105、1．0 ×106和1．0 ×107时，基准算例标准差随发射光线数目和旋转角度的变化关系。随着发射光线数目的增大，相同旋转角对应的统计标准差明显下降，但并非呈现线性关系;同时，在规定旋转角范围内，标准差曲线变得更加均匀平滑，当发射光线数目为1．0 ×107时，最大标准差也仅为1．957 ×10－4。因此，在分析初始相对位置对统计标准差的影响时，发射光线数目均取1．0 ×107根，如图6 所示。研究表明，随着平移距离Δ(－x)的增大，相同旋转角的标准差未呈现出明显变化规律，但整体波动范围略有减小，即角系数的角度均匀性有所提升。即:增大发射光线数目可同时提高角系数的计算精度和角度均匀性，而增大平移距离仅对角度均匀性略有改善。

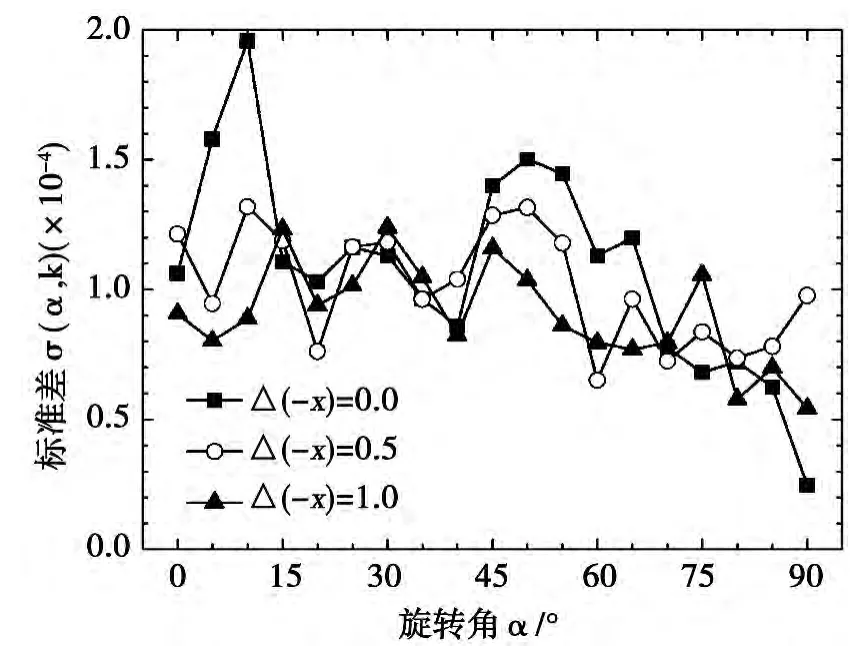
图6 算例Ⅲ初始相对位置对标准差的影响

3 结 论

通过上述计算分析，验证了蒙特卡洛法求解单轴自旋平面对固定平面旋转角系数物理模型及算法的正确性。在此基础上，分析了旋转角度、初始相对位置、发射光线数目等因素对角系数大小和统计标准差的影响。研究表明

(1)当固定平面平移矢量s 不存在－x 方向分量时，角系数随旋转角的增大而减小，且平移距离Δs 越大，角系数变化范围越小，当Δ(+ x)≥0． 5时，大角度角系数出现“零值现象”;

(2)当固定平面平移矢量s 存在－x 方向分量时，对于任意非零平移距离Δs，存在非零旋转角αmax使得角系数取得极大值，且Δs 与αmax呈正相关;

(3)增大发射光线数目可同时提高角系数的计算精度和角度均匀性，而增大平移距离仅对角度均匀性略有改善。

［1］余其铮．辐射换热原理［M］．哈尔滨:哈尔滨工业大学出版社，2000．

［2］岳雷．氧气转炉汽化冷却烟道传热计算［J］．节能技术，2012，30(3):245 －248．

［3］陈朝松，张树林，刘平元，等． 优化壁温计算模型及其在电站锅炉壁温在线监测中的应用［J］．动力工程，2009，29(9):818 －822．

［4］张伟清，宣益民，韩玉阁．单元表面间辐射传递系数的新型计算方法［J］．宇航学报，2005，26(1):77 －80．

［5］王丽，刘志铮，王岳人．低温地板辐射采暖埋管结构尺寸设计实验研究［J］．节能技术，2010，28(1):11 －14．

［6］李景文．开式直筒辐射管辐射换热性能的数值计算［J］．节能技术，2013，31(6):512 －515．

［7］张涛，孙冰． 复杂结构角系数计算方法［J］． 航空动力学报，2009，24(4):753 －759．

［8］王天鹏，王良璧． 一种角系数的数值算法及在室内壁面与窗口间辐射换热中的应用［J］． 兰州交通大学学报，2012，31(6):126 －129．

［9］高亚锋，汤小敏，许孟楠，等． 城市地面对天空热辐射角系数的简化求解［J］． 太阳能学报，2012，33(4):635 －639．

［10］M．R． Vuji i ，N．P． Lavery，S．G．R． Brown．View Factor Calculation Using the Monte Carlo Method and Numerical Sensitivity［J］． Communications in Numerical Methods in Engineering，2006，22(3):197 －203．

［11］M． Mirhosseini，A． Saboonchi． View Factor Calculation Using the Monte Carlo Method for a 3D Strip Element to Circular Cylinder［J］．International Communications in Heat and Mass Transfer，2011(38):821 －826．

［12］Jose M． Cabeza － Lainez，Jesus A． Pulido － Arcas．New Configuration Factors for Curved Surfaces［J］． Journal of Quantitative Spectroscopy ＆ Radiative Transfer，2013(117):70 －80．

［13］Alireza Bahadori，Sohrab Zendehboudi，Gholamreza Zahedi，et al．． Estimation of Configuration Factor for Radiation from a Rectangle to a Parallel Small Element of Surface Lying on the Perpendicular to a Corner of the Radiator［J］．Chemical Engineering Communications，2014，201(3):287 －299．

［14］谈和平，夏新林，刘林华，阮立明．红外辐射特性与传输的数值计算［M］． 哈尔滨:哈尔滨工业大学出版社，2006．

［15］J． R． Howell． A Catalog of Radiation Heat Transfer Configuration Factors (Version 4)［M］． New York:McGraw Hill，2010．

［16］Yong Shuai，Hao－Chun Zhang，He －Ping Tan．Radiation Symmetry Test and Uncertainty Analysis of Monte Carlo Method Based on Radiative Exchange Factor ［J］． Journal of Quantitative Spectroscopy ＆ Radiative Transfer，2008(109):1281 －1296．