一维热扩散方程的格子Boltzmann 方法分析

吴国忠，袁兆成，齐晗兵，李 栋，刘 杰

(东北石油大学 土木建筑工程学院，黑龙江 大庆 163318)

近年来，格子Boltzmann 方法(LBM)在求解偏微分方程领域发展很迅速，特别是求解Navier －Stokes 方程获得很大成功。由于Boltzmann 方法具有物理图像清晰、边界条件容易处理以及并行性能好等优点，被广泛应用于微/纳米尺度流［1］、多孔介质流［2］、多相多质流［3］和晶体生长［4］等许多领域。

扩散过程在物理、化学、生物等许多领域中起着很重要的作用。热扩散方程是描述传热过程的一个重要方程，但在复杂的边界和初始条件下，解析求解是很困难的。许多学者利用格子Boltzmann 方法求解扩散问题，并取得了很多成果。刘慕仁等人给出了求解一维有源扩散方程的格子Boltzmann 模型，确定了局部平衡函数Chapman－Enskog 展开的待定系数［5］，他们还利用格子Boltzmann 方法求解了一维对流扩散方程，确定了方法中的粘滞系数与对流系数的关系［6］。徐世英等人利用浓度分布的Chapman－Enskog 展开及多尺度技术，得出了Tyson 反应扩散的反应物和催化剂随时间的浓度空间分布值［7］。本文在前人的研究基础上，提出了格子Boltzmann 方法求解一维热扩散方程的有效数值方法。

1 热扩散方程的Boltzmann 模型

一维热扩散方程表达式

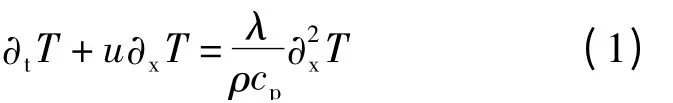
式中

T——温度，要求T≥0;

u——速度;

λ/ρcp——热扩散系数;

λ——导热系数;

ρ——密度;

cp——定压比热容。

1．1 平衡态分布函数

将一维空间离散成均匀的线性格子，每个节点与相邻的节点相连。将速度ca=cea离散为三个方向，ea可取值－1，0，1，分别对应粒子速度方向向左、不动和向右三种情况。c=Δx/Δt 为粒子迁移速率，3 －速格子模型如图1 所示。

图1 3 －速格子模型示意图

用fi(x，t)表示沿ea方向的粒子分布函数，表示在时间t 时，在位置x 处粒子出现的概率，应有fi≥0，宏观量T 定义为

式中 feq

i ——平衡态分布函数。

根据统计物理，分布函数遵守以下格子Boltzmann 方程

式中 τ——弛豫时间。

式(3)也称LBGK(Lattice BGK，简称LBGK)方程，为满足稳定性条件，要求τ≥0．5。

由式(3)可知，只要得到feq(x，t)就可以得出以后时间的分布函数f(x，t)。由LBGK 方程恢复宏观方程的关键是选择适当的平衡态分布函数。由统计力学可知，在局域平衡条件下，分布函数可表示为局域平衡量的函数，考虑到ea的对称性，将平衡态分布函数表示为

式中 a0、a1、a2——待定系数。

1．2 格子Boltzmann 方程

对式(3)的左侧项进行空间和演化时间的Taylor 级数展开，取其到二级项可得

应用Chapman－Enskog 方法对时间系数、空间系数和分布函数进行多尺度展开，可得到

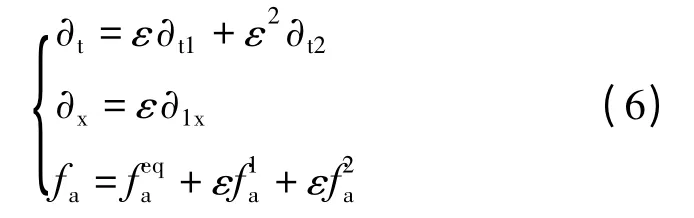
式中 ε——小参量。

将式(6)代入式(5)，在ε 一阶小量下有

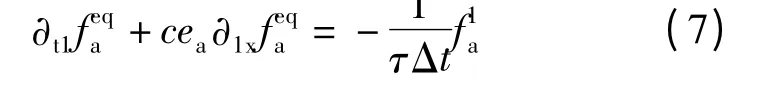
在ε 二阶小量下有

将式(7)和式(8)分别对下标求和得出

由此得到的式(9)、式(10)即为时间t1和t2尺度下的密度平衡方程。

1．3 宏观热扩散方程

将式(4)代入式(2)，可以得到

为了在t1尺度上恢复方程的对流项，令

由式(9)、式(12)得到

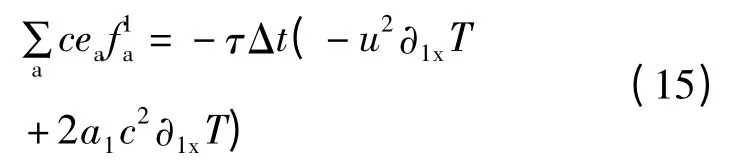
由式(7)和式(14)得到将式(15)代入式(10)，得到

将式(14)乘以ε，式(16)乘以ε2，两式相加便可回到宏观尺度下的方程(1)。令，则

由式(11)、式(13)和式(17)可得出待定系数

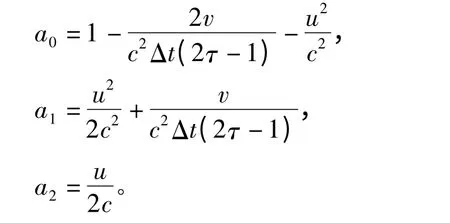
2 数值实验

为验证得到的热扩散方程的Boltzmann 模型，采用文献［6，8］中的算例，进行了验证性模拟实验。

2．1 验证算例1

算例1 中热扩散方程的边界条件为第一类边界条件且为恒温，具体的控制方程

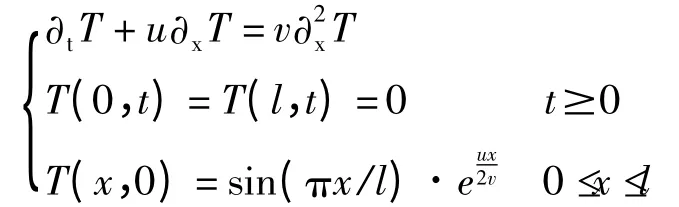
算例1 的解析解在文献［6］中已给出

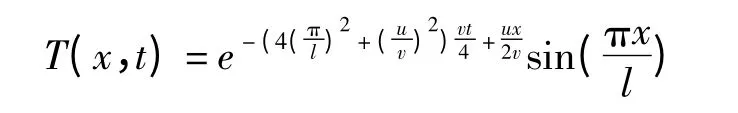
算例1 中热扩散方程的格子Boltzmann 模型求解参数:τ =1． 2，u =0． 2，v =0． 5，时间步长Δt =0.01，空间步长Δx=0．1，粒子的迁移速率为c=10，总长度l=40，t 分别为280、290、300 和310。

图2 给出了不同时刻t 下算例1 的模拟值与解析解。从图中可以看出，t 为280、290、300 和310时，模拟值与解析解的最大绝对误差分别为1．31E－04、8．70E－05、7．20E －05 和7．00E －06，从而说明数值解与解析解吻合良好。

网格数目对模拟结果精度有一定的影响。本文分析网格数目为80、200 和400 时，对计算精度的影响情况。

图2 不同时刻下算例1 的模拟值与解析解的比较

表1 为τ=1．2，u=0．2，v=0．5，时间步长Δt=0．01，t =300，总长度l =40，空间步长Δx 分别为0.5，0．2 和0．1 时，各个节点在不同网格数目下的解析解与数值解及其绝对误差。从表中可以看出，网格数目分别为80、200 和400 时的最大绝对误差分别为3．02E－03、3．31E－04 和7．00E－05。由此可见，随着网格的细化，模拟结果的绝对误差越来越小。

2．2 验证算例2

算例2 中的热方程的边界条件是随着时间t 变化的，具体方程如下该问题的解析解在文献［8］中已给出

表1 各节点在不同网格数目下的解析解与模拟值及其绝对误差

图3 给出了不同时刻t 下算例2 的模拟值与解析解。从图中可以看出，t 分别为1、4、7 和10 时的最大绝对误差分别为6．21E－04、4．62E－04、4．98E－04 和5．09E－04，从而说明数值解与解析解吻合良好。

图3 不同时刻下算例2 的模拟值与解析解的比较

3 结语

本文基于格子Boltzmann 方法，采用Chapman－Enskog 展开和多尺度技术，建立了求解一维热扩散方程的D1Q3 模型，模型的数值解与文献的解析解吻合良好，其两者的误差随网格细化而大幅度减小，从而说明了本文模型可用于求解一维热扩散方程。

［1］Raabe D． Overview of the lattice Boltzmann method for nano－ and microscale fluid dynamics in materials science and engineering［J］． Modeling and Simulation in Materials Science Engineering，2004，12(6):R13 －R46．

［2］Tang G H，Tao W Q，He Y L． Gas slippage effect on microscale porous flow using the lattice Boltzmann method［J］．Physical Review E，2005，72(5):056301．

［3］Grunau D，Chen S，Eggert K． A lattice Boltzmann model for multiphase fluid flows［J］． Physics of Fluids，1993，5(10):2557 －2562．

［4］Miller W，Succi S，Mansutti D． Lattice Boltzmann model for anisotropic liquid－solid phase transition［J］．Physical review letters，2001，86(16):3578 －3581．

［5］邓敏艺，刘慕仁，李珏，等． 一维有源扩散方程的格子Boltzmann 方法［J］． 广西师范大学学报:自然科学版，2000，18(1):9 －12．

［6］刘慕仁，何云，陈若航，等． 一维对流扩散方程的格子Boltzmann 方法［J］．广西科学，1999，6(3):168 －169．

［7］徐世英，卫玉敏，吴春光，等．一维Tyson 反应扩散系统的格子Boltzmann 方法模拟［J］．计算机与应用化学．2008，25(5):537 －540．

［8］李贵艳，罗东升． 对流扩散方程的数值计算［J］． 数学杂志，2009，29(2):186 －190．