行星滚柱丝杠副齿轮变位系数的优化

高 扬, 杨家军，梁 汉，邓 波, 朱继生

(1 华中科技大学机械科学与工程学院，湖北 武汉 430074；2 中船重工七二二研究所, 湖北 武汉 430072； 3 山东博特精工股份有限公司，山东 济宁 272071)

行星滚柱丝杠副齿轮变位系数的优化

高 扬1, 杨家军1，梁 汉1，邓 波2, 朱继生3

(1 华中科技大学机械科学与工程学院，湖北 武汉 430074；2 中船重工七二二研究所, 湖北 武汉 430072； 3 山东博特精工股份有限公司，山东 济宁 272071)

变位系数是行星滚柱丝杠副设计的重要参数，将内齿圈和滚柱端齿的变位系数作为设计变量，通过对其失效形式的分析，确定优化设计的目标函数；通过对几何结构分析，确定一系列约束条件,建立变位系数的优化数学模型，采用复合形法求解方法获得最佳变位系数。

行星滚柱丝杠； 齿轮； 变位系数； 复合形法

行星滚柱丝杠是一种将旋转运动转换为线性运动的机械装置。它与滚珠丝杠相比，具有承载能力大、效率高、寿命长等特点，目前已被广泛应用于数控机床、工业机器人、航空航天等领域。行星滚柱丝杠副内部结构较为复杂，部件精度、可靠性要求高，其啮合齿变位系数的优化也一直是其设计过程中的重要问题，现实中常常因为变位系数选择不当，造成产品精度达不到要求或可靠性不高。为进一步优化行星滚柱丝杠副性能，须探索一个更合理的设计方法解决这个问题。

1 行星滚柱丝杠的传动原理分析

行星滚柱丝杠主要由丝杠、滚柱、螺母、内齿圈、保持架等组成(图1)[1]。

1-滚柱2-内齿圈；3-丝杠；4-保持架；5-螺母

其工作原理为：丝杠、滚柱和内齿圈可以分别视为太阳轮、行星轮和中心轮，当螺母周向固定而丝杠旋转时，滚柱围绕丝杠做行星运动，通过滚柱与丝杠的螺旋传动，把丝杠的回转运动转换为螺母的直线运动。滚柱端齿轮可以保证丝杠、螺母与滚柱间啮合传动的同步性，避免发生干涉，也可以在高速重载的时候减轻螺纹传动的负荷[2]。

行星滚柱丝杠副的机构简图如图2所示。

1-丝杠 2-滚柱；3-螺母；2′ -滚柱端齿轮(行星齿轮)；4-内齿圈齿轮(与2’啮合)；H-滚柱丝杠副的螺纹副；dn-内齿圈齿的公称直径；dr-滚柱端齿的公称直径；ds-丝杠的公称直径；zn-内齿圈齿的齿数；zr-滚柱端齿的齿数

图 2 行星滚柱丝杠副机构简图

2 变位系数的选择原则

从避免失效的角度来确定变位系数的选择原则。行星滚柱丝杠作为高速重载的传动部件，其内齿圈和滚柱端齿轮在工作中可能会出现齿面点蚀、齿面胶合、磨损等多种失效形式。综合分析，其变位系数的选择有以下三个原则：

1) 为了尽可能提高滚柱端齿轮和内齿圈的接触强度，避免齿面点蚀等失效形式，应使啮合点齿廓综合曲率半径增大，即相啮合齿的变位系数之和应尽量大；

2)为了尽可能提高滚柱端齿轮和内齿圈的弯曲强度，避免轮齿折断等失效形式，应使相啮合齿轮的弯曲强度趋于平衡，并尽量减小齿形系数，相应地限制了变位系数；

3)为了尽可能提高齿面抗胶合和耐磨性能，应使啮合齿在啮合过程中滑动系数尽量相等，相应地限制了变位系数。

3 目标函数的建立

根据行星滚柱丝杠副滚柱端齿和内齿圈变位系数的选择原则，可以确定变位系数优化过程的目标函数[3]。

考虑到啮合齿的接触强度，应使变位系数之和尽量大，由无侧隙啮合方程可导出目标函数

(1)

式中：α为分度圆压力角，取20°；α′为啮合角；z1为内齿圈齿数；z2为滚柱端齿齿数。

考虑到齿轮弯曲强度，应使啮合齿弯曲强度趋于平衡，可得目标函数为

minf2(x)=σF1-σF2

(2)

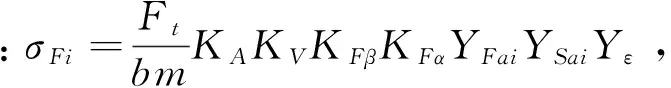
考虑到提高齿面抗胶合和耐磨性能，应使啮合齿在啮合过程中滑动系数尽量相等，滑动系数是滑动弧与齿廓所走过的弧长比。目标函数为

minf3(x)=η1-η2

(3)

在该优化问题中，内齿圈的变位系数x1和滚柱端齿的变位系数x2是相关的，故可取x1为设计变量，其他参数为x1的函数，则总目标函数为

minf(x1)=

-w1(x1+x2)|w2(σF1-σF2)|w3(η1-η2)

(4)

式中，wi(i=1,2,3)为加权因子，表示分目标函数的重要程度。

为了求解方便，将此多目标规划问题化为单目标规划问题，过程如下。

1)采用函数y=x/2π-sinx(0≤x≤2π)，将分目标函数转化为规格化目标函数。

式中qi、pi分别为设计指标的上下限。

2)利用容限法求解加权因子。目标容限Δfi=(qi-pi)/2(i=1,2,3)，目标函数的加权因子wi=1/(Δfi)2(i=1,2,3)。所以原目标函数式(4)可以改写为

minf(x1)=

-w1fr1(x1)+w2fr2(x1)+w3fr3(x1)

(5)

4 约束条件的确定

为了确保滚柱丝杠副稳定运行，不发生干涉，并具有一定的可靠性和寿命。根据行星滚柱丝杠副的几何结构，可以确定优化过程的约束条件[6-7]。

1)齿顶圆大于基圆约束

(6)

(7)

2)重合度约束

(8)

式中：αa1为内齿圈齿顶圆的压力角；αa2为滚柱端齿齿顶圆的压力角。

3)齿廓干涉约束

g4(x1)=z1(δ1+invαa1)-z2(δ2+invαa2)

+(z2-z1)invα′≥0.05

(9)

4)齿顶距约束

g5(x1)=Ra2-Ra1+a′-0.1m≥0

(10)

式中：Ra1为内齿圈齿顶圆半径，Ra2为滚柱端齿齿顶圆半径；a′为啮合中心距；m为模数。

5)齿根隙约束

g6(x1)=Ra2-Rf1-a′-0.1m≥0

(11)

式中，Rf1为内齿圈齿根圆的半径。

5 复合形法的求解

由以上分析可得，求解x1的数学模型为

minf(x1)

gu(x1)≤0(u=1,2,…,6)

(12)

复合形法是求解约束优化问题的直接方法之一，是无约束最优化问题单纯形法的推广。由于该优化问题只有不等式约束，所以可以用该方法求解，求解步骤如下。

2)设置初始复合形顶点数为9，在可行域内产生分布均匀的伪随机数，以确定复合形的其中一个顶点，检查这个点是否在可行域内，如果不在，则需要重新选点。用同样的方法产生全部的顶点；

5)计算反射点函数值，若反射点在可行域内，则与最坏点的函数值比较，根据结果调整反射点，直到满足约束条件。

重复步骤3)-5)，直到各顶点的距离达到精度要求为止。

6 应用示例

采用上述理论方法，对如表1所示国外某型号行星滚柱丝杠进行优化设计。

表1 国外某型号行星滚柱丝杠副基本参数

经编程计算得到：

2.68≤f1(x1)≤5.38，0≤f2(x1)≤33.2，0≤f3(x1)≤3.08；同时可以得到w1=0.35，w2=0.01，w3=0.81；经过优化得到：x1=0.21，x2=-0.16。优化后的参数在满足约束条件的前提下，实现了目标函数最优。

7 结束语

本文采用行星滚柱丝杠副内齿圈和滚柱端齿变位系数的优化方法，在确保行星滚柱丝杠副稳定运行的同时，最大限度提高其齿轮部分的寿命和可靠性，从而提高了行星滚柱丝杠副在高速重载条件下的工作能力，降低了设计成本，减少了设计周期，为行星滚柱丝杠的设计提供了一种较为有效的方法。

[1] 刘 更，马尚君，佟瑞庭,等.行星滚柱丝杠副的新发展及关键技术[J]. 机械传动，2012，36(05):103-108.

[2] 韦振兴，杨家军，朱继生,等.行星滚珠丝杠副的结构参数优化分析[J]. 机械传动，2011，35(06):103-108.

[3] 邱宣怀.机械设计[M].北京:高等教育出版社，1991:167-204.

[4] 孟彩芳.机械原理电算分析与设计[M].天津:天津大学出版社，2000:144-159.

[5] 张春燕，唐迎春，姚文席.三环减速器内啮合变位系数的研究[J].北京石油化工学院学报，2008，16(01):31-34.

[6] 余跃海.少齿差内啮合齿轮的计算机辅助几何设计及参数优化[D].天津：天津大学，2005.

[7] 罗中华.最优化方法及其在机械行业中的应用[M].北京:电子工业出版社，2008:91-94.

[责任编校： 张 众]

Optimization of Planetary Roller Screw Gear Modification Coefficient

GAO Yang1, YANG Jiajun1, LIANG Han1, DENG Bo2, ZHU Jisheng3

(1SchoolofMechanicalSci.andEngin.,HuazhongUniv.ofSci.andTech.,Wuhan430074,China;2 722ResearchInstituteofCSIC,Wuhan430079,China;3ShandongBESTPresionCO.LTD,Jining272071,China)

The modification coefficient, an important parameter for the design of planetary roller screw, The modification coefficient of internal gear ring and roller end gear was used as design variables in this paper. The objective function of optimization design was determined through analyzing the failure mode. Based on the analysis of geometric structure, a series of constraints were determined, and then an optimization mathematical model of variable coefficient was established. By using the complex method, the best modification coefficient can be determined.

planetary roller screw; gear; modification coefficient; complex method

2015-04-20

高 扬(1991-)，男，河南濮阳人，华中科技大学硕士研究生，研究方向为智能机械与数字化装备

1003-4684(2015)04-0058-03

TH13

A