一种无衍射光莫尔条纹的计数方法

翟中生，严昌文，吕清花，王选择

(湖北工业大学机械工程学院，湖北武汉430068)

无衍射光(non-diffracting beams)由于其中心光斑的大小、形状不随传播距离发生变化的特性备受人们关注。无衍射光近年来已成为研究的热点［1-2］，如:华中科技大学的周莉萍教授利用无衍射光实现了一种新型激光三角测量系统［3］;北京航空航天大学的王中宇教授用无衍射光代替激光作为光源，来完成表面形貌的三维测量［4］。无衍射光技术也可应用到自由度的测量中［5］。在利用无衍射光测量多自由度运动误差时，确定无衍射光中心光斑的位置成为测量的关键。由于莫尔条纹的放大作用，可以利用无衍射光莫尔条纹技术来定位无衍射光中心光斑。华中科技大学的赵斌教授利用无衍射光莫尔条纹法进行空间直线度的测量［6］，同时利用计算机产生数字的环形光栅与环形无衍射光产生莫尔条纹，通过改变数字环形光栅的相位来确定无衍射光的中心光斑位置［7］。在无衍射光莫尔条纹法定中心的应用中，文献［7］只运用了一束无衍射光，而本文则利用两束无衍射光得到莫尔条纹，通过莫尔条纹的条数，得到莫尔条纹数量与两束无衍射光中心点距离的关系，由此来确定被测无衍射光的中心光斑位置。

1 无衍射光莫尔条纹的形成

目前得到无衍射光的方法有很多，而之所以采用轴锥镜是因为其能量利用率高和制作成本低的特点，同时在测量方面，轴锥镜又有着稳定的线焦，产生的无衍射为零阶本赛尔函数形式的同心圆环(图1a)。这一族同心圆环中，中心圆是最亮的点。图1a所示，当平行光射入轴锥镜时镜后形成的不同区域，Zmax为光强的最大范围。在Zmax范围内光强随Z值的增大而增大。通过轴锥镜得到合适的无衍射光，并将无衍射光作为测量光。

图1 无衍射光的产生

从技术角度上来说，莫尔条纹是两条或者两个物体之间以恒定的角度和频率发生干涉的视觉结果。

为了研究无衍射光莫尔条纹的计数法，首先通过轴锥镜得到零阶贝塞尔形状的同心圆环(即无衍射光)，然后通过一个简单的光路(图2)得到两束无衍射光的干涉，从而得到莫尔条纹。从图2可见，He-Ne激光器发出的光经过准直扩束后射入轴锥镜，再由轴锥镜射入到分光棱镜1中，此时通过分光棱镜1分光，得到两束无衍射光:一束无衍射光经过反射镜2、分光棱镜2后由CCD相机接收;另一束无衍射光进过反射镜1射入到直角棱镜中，再由直角棱镜反射到分光棱镜2，最后也被CCD相机接收。这样，CCD相机中就有两束无衍射光，这两束衍射光将会干涉产生莫尔条纹，同时产生的莫尔条纹图像将被CCD相机采集。其中经过反射镜2、分光棱镜2的无衍射光作为参考光束，经过直角棱镜、分光棱镜2的无衍射光作为被测光束，由于直角棱镜在竖直方向上的移动会造成两束无衍射光中心距离的变化，因此被测光束的中心光斑的位置也将发生变化。

图2 无衍射光莫尔条纹的产生

2 无衍射光莫尔条纹的数学模型

图2中，轴锥镜后产生的无衍射光束经过分光棱镜分成两束无衍射光，设两束光程分别为无衍射光的产生Z1和Z2，C1和C2为CCD相机上两束无衍射光的中心点，在CCD面上的极半径分别为r1和r2，可得到两束无衍射光在CCD上的光强近似值

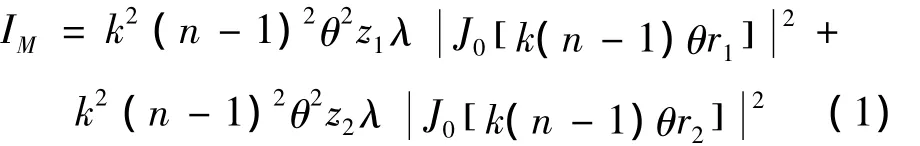
产生的减莫尔条纹的序列有

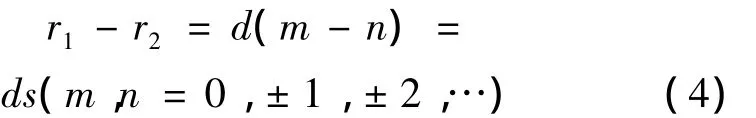
为了分析方便，设C1、C2在y轴上(C1x=C2x=0)，原点在中心线上(|C2y－C1y|=2Δ)，由式(2)、(3)和(4)可计算出莫尔条纹的暗条纹轨迹为

从上式可看出，莫尔条纹的暗条纹轨迹为椭圆族或双曲线族。

3 莫尔条纹计数方法

两束无衍射光形成的莫尔条纹的形状和条纹数受中心位置影响，因此确定无衍射光莫尔条纹的数量是关键。

等间距的无衍射光束的明暗条纹的间距可看成光栅常数d。为了便于分析，假设测量光束的中心点C2在y方向上有一偏移量C2y(图3)。中心间距用光栅常数d表示

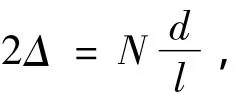
式中N为正整数，l=1，2，3…。

图3 两束无衍射光产生的莫尔条纹原理图

由式(5)可得

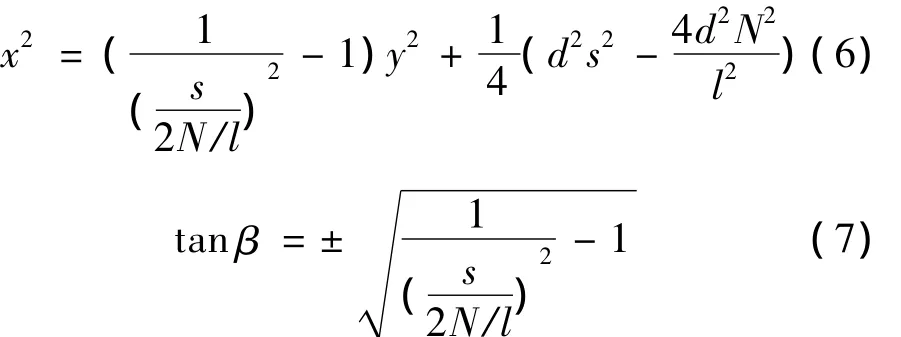
式中，β为直线族与y轴的夹角。在xy坐标系中，莫尔条纹沿坐标原点对称分布，所以研究莫尔条纹变化规律时，取β从竖直方向上0°～180°范围即可。

由式(7)可知，s=0时，tanβ= ∞，β =90°;s=时，tanβ=0，β=0°，因此可以得到在第一象限内有条莫尔条纹，那么在360°范围内总莫尔条纹数S=。a

4 仿真及图像处理

通过对图2的光路进行仿真，得到如图4所示的无衍射光莫尔条纹图像。由于直角棱镜在竖直方向上的位移导致两束无衍射光中心光斑距离的变化。从图6中可明显看出，两束无衍射光中心距的改变会引起莫尔条纹数量的变化。

通过图4的仿真结果可以看到，莫尔条纹的频率要小于无衍射光的频率，因此对图4中仿真得到的图进行频域空间的增强。在Matlab中首先对图4进行傅立叶变化得到频域空间，然后选择高斯低通滤波器，最后将增强的图像通过傅立叶逆变换转换回图像空间，得到的图像如图5所示。

为了进一步得到莫尔条纹数，将图5进行二值化处理，得到二值化图像，定义在图像中的一个内乘圆，统计在该内圆上，图像灰度值变化的次数，让计算机自动记录图像中由黑到白的变换次数，则变化的次数就是莫尔条纹数。图6为二值化后的莫尔条纹图，表1为通过程序统计得出的莫尔条纹数量。

图4 两束无衍射光产生的莫尔条纹仿真结果

图5 高斯滤波后的傅立叶逆变换图

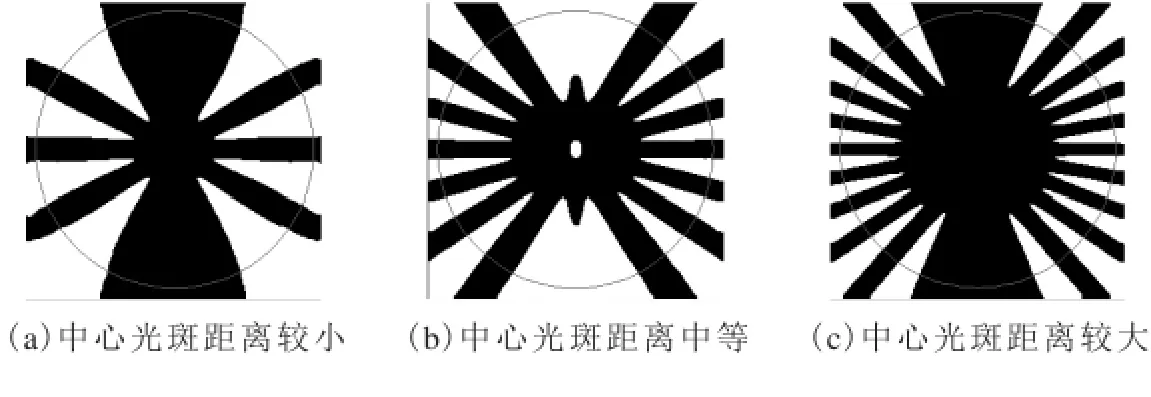
图6 二值化后的莫尔条纹图

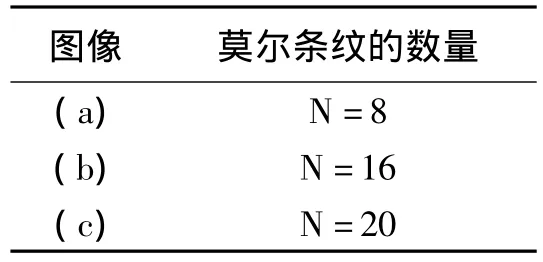
表1 莫尔条纹数结果

5 结论

本文用一种无衍射光莫尔条纹的计数方法来定位无衍射光中心光斑的位置。本方法的特点是通过两束无衍射光的干涉产生了莫尔条纹，由莫尔条纹的数量关系得到两束无衍射光的中心距，由此进一步确定被测无衍射光的中心光斑位置。本文中莫尔条纹数学模型的两束无衍射光中心点在y轴上保持一致，同样如果中心点在x轴上也适用本文的结论。通过确定的无衍射光中心光斑位置，可以进一步对多自由度在二维角度上的测量进行研究，因此本文对无衍射光莫尔条纹在精密测量的应用中有一定借鉴意义。

［1］ 王中宇，周 聪，张 朵.无衍射光技术在瞄准系统中的理论与原理实验［J］.北京航空航天大学学报，2006，32(11):1 337-1 340.

［2］ 陈 慧，赵 斌.无衍射光电子标靶及误差分析［J］.光电工程，2011，38(02):34-40.

［3］ 周莉萍，高咏生，李 柱.基于无衍射光及虚拟探测器的三角测量系统［J］.华中科技大学学报，2001，29(01):8-10.

［4］ 王中宇，王 倩，孟 浩.基于无衍射光的表面粗糙度三角测量及其灰色评定方法［J］.应用光学，2011，32(05):909-912.

［5］ 赵 斌.无衍射光莫尔条纹法直线度测量仪［J］.仪器仪表学报，2003，24(01):75-77.

［6］ 赵 斌.无衍射光莫尔条纹空间直线度测量的原理与实验［J］.计量学报，2002，23(02):81-86.

［7］ 赵 斌.环栅图像的数字莫尔条纹扫描定中方法［J］.光学精密工程，2002，10(02):19-24.

［8］ Madanipour K，Tavassoly M T.Moire fringes as two-dimensional autocorrelation of transmission function of linear gratings and its application formodulation transfer function measurement.Opt Lasers Eng，2010，48(01):43-47.

［9］ Weon-Jae R，Young-June R，Sung-Hoon B，etal.A study on the 3-D measurement using digital projection moiré method.Optik-Int J Light Electron Opt，2008，199(10):453-458.

［10］Xiao X，Kang Y，Hou Z，etal.Displacement and strain measurement by circular and radial gratings moirémethod.Exp Mech，2010，50(02):239-244.