压电微固体模态陀螺的安装技术*

韦 念，吴校生，刘 武，陈文元，崔 峰，张卫平

(上海交通大学 微纳科学技术研究院，上海200240)

0 引 言

陀螺是一种用以测量角速度和角位移的传感器件，在航天、航空、航海以及制导等领域中有着广泛的应用。2006 年，在土耳其Istanbul 召开的MEMS 会议上，日本学者Maenakae K 等人首次提出了一种基于压电体高阶振动模态的新型压电固态陀螺［1］，文中称之为压电微固体模态陀螺(PMMG)。与传统的机械陀螺相比，该陀螺内部不存在作整体运动的部件和弹性支撑结构，因此，这种类型的陀螺抗冲击、抗震动能力强，对真空封装没有特别要求，且具有体积小、功耗低、重量轻等特点。为确保其能长期、稳定的工作，陀螺应封装在密封腔室内来隔离外界环境对它的影响。

近年来，陀螺的封装技术受到越来越多的关注。文献［2］分析了支撑柔度对品质因数(Q)和压阻换能效率的影响;文献［3］提出了线性声波带隙阵列支撑方法来降低寄生模态对MEMS 谐振器的影响;通过将支撑与反射体的有效结合，支撑带来的损失可以降到最低［4］;而在ALN 谐振器中，使用平边取代原来的凸边，可将通过支撑耗散的能量减到最小［5］。然而，大多数文献都在研究如何通过改善支撑来提高Q 值，并没有涉及到封装技术对参考振动模态的影响，而参考模态的优化对于陀螺性能的提高至关重要。

本文首先从理论上对压电型微固体模态陀螺的工作原理和所需参考振动模态进行了分析，然后采用有限元分析方法分析了支撑点的位置与接触面积对陀螺参考振动模态参数的影响。

1 压电微固体模态陀螺的工作原理

如图1 为压电微固体模态陀螺的总体结构示意图，L，W，H 分别表示压电振子的长(x 轴)、宽(y 轴)，高(z 轴，极化方向P)。陀螺的核心部件是压电长方体振子，上下表面分别分布着驱动电极(D+，D－)，检测电极(S1～S8)和参考电极(R1～R4)。工作时，在驱动电极D+，D－上施加等幅、同频(工作模态频率)、反相的交变电压，使陀螺处于一种特殊的共振模态，当有角速度输入时，利用科氏效应和压电材料的压电效应进行检测。该共振模态的特殊性在于:首先，为了保证感应的科氏力沿同一个方向(如z 轴方向)，参考振动中各质点的振动方向必须沿着与之相垂直的另一个方向(如y 轴方向);其次，当外界有角速度输入的时候，由参考振动感应科氏力的感应振动必须是某个方向上的挤压运动或拉伸运动，同时这个挤压或拉伸运动的方向和压电体极化方向一致，以便在压电体表面感应出能检测的表征外界输入角速度大小的压电电荷;感应振动的运动特性要求参考振动也是做挤压或拉伸运动。

如图1 所示，在激励电压的驱动下，由于逆压电效应产生同频率的参考振动，且相邻两条边上的振动方向相反，相对两条边上的振动方向相同，图中，u 即表示棱边的振动方向。当沿着x 轴方向上有角速度输入时，由于科氏效应，会在z 方向产生科氏力Fc，从而在z 方向产生相应的拉伸或压缩运动，即检测振动。y 轴上的一对检测电极(如S1，S2)在参考振动模态下振幅相同，但运动方向相反，科式效应下它们会受到相反的科氏力，导致这两个检测电极上的输出信号朝相反的方向变化，且变化值与外界输入角速度呈正比，据此通过外围电路对感应电荷或电压进行放大和量化，可以得到外界输入角速度的大小。

图1 压电微固体模态陀螺的结构与工作原理Fig 1 Structure and working principle of PMMG

2 安装技术

这部分主要借助有限元软件Ansys 对安装技术与陀螺参考模态之间的关系进行仿真分析，以期找出合适的支撑方法。本文选用压电单元solid226 来模拟PZT—5H 作为压电陀螺的基体材料，PZT—5H 的材料属性如下:密度7 500 kg/m3，相对介电常数ε11=762.5，ε33=663.5，压电常数矩阵e31=－5.202 79 C/m2，e33=15.080 4 C/m2，e16=12.717 9 C/m2，弹性系数矩阵c11=13.9×1010N/m2，c12=7.8×1010N/m2，c13=7.4×1010N/m2，c33=11.5×1010N/m2，c44=2.6×1010N/m2，c66=3.1×1010N/m2。

仿真所用模型尺寸为5 mm×4 mm×3 mm，采用Block Lanczos 算法对其进行模态分析。由于压电振子各个面中心点(节点)位移基本为零［6］，故可将支撑点设置在这些位置处来减少能量损失。为方便起见，假设支撑点为正方形。图2(a)，(b)分别表示压电微固体模态陀螺单点支撑与两点支撑的示意图，阴影部分为支撑点与陀螺的接触面积，d表示支撑点的边长。

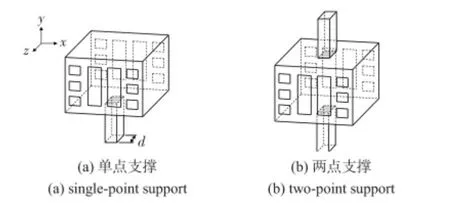
图2 压电微固体模态陀螺的两种支撑示意图Fig 2 Two kinds of support of PMMG

2.1 单点支撑

按照图2(a)所示支撑陀螺，利用有限元谐振分析观察支撑点边长d 对参考振动的影响。图3 分别给出了各个电极上(除驱动电极)输出电压幅值和电压峰值频率与支撑点边长的关系图，其中，虚线表示参考电极，实线表示检测电极。

图3 单点支撑下支撑点尺寸对参考模态的影响Fig 3 Effect of supporting point size on reference modal under single-point support

从图3(a)可以看出，单点支撑的情况下，四个参考电极上的输出电压始终保持一致，均随着支撑接触面积的增大而减小;但y 方向上相邻的两个检测电极输出电压出现差异，靠近支撑点一侧的检测电极电压逐渐减小，而远离支撑点一侧的检测电极电压逐渐增大，最终两者的差异达到0.46 V，这是由于所有参考电极离支撑点的距离相同，支撑点对其限制情况是相同的，而y 方向上相邻的检测电极距离支撑点远近不同，受到的节点限制也不同。由图3(b)可知，各电极上的谐振频率随着支撑点边长的增大而增大。支撑面积的增大会使得陀螺表面被限制的节点增多，随之带来陀螺刚度和谐振频率的增大，图中参考电极与检测电极上的峰值频率略有差异，可能是由于网格划分造成。单点支撑下，y 轴上的一对检测电极感应出的电压并不相同，这种不对称性不符合参考振动模态的要求，会影响到后续的科氏力检测，所以，不适合采用单点支撑的安装方式。

2.2 两点支撑

根据以上结论，采用如图2(b)所示的两点支撑，图4 为陀螺的参考振动与支撑点大小的关系图。由图可知，检测电极上的感应电压全都相同，一致性比较好，随着支撑点面积的增大，各个电极上的输出电压、谐振频率也越来越大。

图4 两点支撑下支撑点尺寸对参考模态的影响Fig 4 Effect of supporting point size on reference modal under two-point support

图5 、图6 分别给出了参考模态参数与支撑点位置关系曲线图。由图5 可知，支撑点沿x 方向移动，导致x 方向上电极输出电压的不对称，且支撑点偏离中心越远，电压差越大，但两个相邻电极的输出电压关于原点呈反对称性;参考电极、检测电极的谐振频率基本一致，并随x 方向位移量的增大而增大，与位移方向无关，即谐振频率关于横坐标原点对称，与理论分析一致的。

由图6 可知，支撑点沿z 方向移动，导致z 方向上电极输出电压的不对称，随着偏移量的增大，电压差总体上呈增大趋势，各个电极的谐振频率随z 方向位移量的增大而增大。由图5(b)和图6(b)可知，z 方向上的偏移还会导致z方向上电极谐振频率的不一致，而且同一电极的谐振频率关于横坐标原点也不对称。

图7 是用于陀螺驱动和检测的整个电路系统以及所采用的两点安装方法。

图5 支撑点沿x 轴方向移动对参考模态的影响Fig 5 Effect of x-axis displacements of supporting point on reference modal

图6 支撑点沿z 轴方向移动对参考模态的影响Fig 6 Effect of z-axis displacements of supporting point on reference modal

图7 PMMG 工作的整个电路系统和两种封装方法Fig 7 Overall circuit system of PMMG and two packaging methods

从上述分析可知，参考电极、检测电极上的输出电压和对应的谐振频率会随着支撑点接触面积的增大而增大，所以，应尽量减小接触面积，使用点支撑;支撑点一旦偏离面心，电极的输出电压会出现不对称，而谐振频率会随着位移量的增大而增大，所以，支撑陀螺时尽量保证支撑点在面心位置。与支撑点沿x 轴方向的移动对参考模态的影响相比，z 方向的偏移对其影响更显著，包括z 方向上电极输出电压和谐振频率的不对称，这可能是由于陀螺z 方向的尺寸要比x 方向的尺寸小，同样的位移量下z 方向的变化对陀螺的影响更大。

3 结 论

本文对压电微固体模态陀螺的工作原理和参考振动模态进行了分析。利用有限元法分析了支撑点位置与接触面积对参考模态的影响，分析结果表明:单点支撑的安装方式会导致检测电极输出电压不对称，两点支撑能很好地避免这个问题。在两点支撑下，随着支撑点接触面积的增大，参考电极、检测电极输出电压及它们的谐振频率逐渐增大，实际操作中应尽量减小支撑面积，使用点支撑;支撑点位置的变化也会带来相应的输出电压、谐振频率的不对称，在位移相同的情况下，使得检测电极与参考电极上的频率值出现差异，而且支撑点沿z 轴方向的位移对陀螺参考模态的影响更大，这会对陀螺的闭环驱动和科氏力检测产生不利影响，本文的研究为压电微固体模态陀螺的安装方法提供了理论依据。

［1］ Maenaka K，Kohara H，Nishimura M，et al.Novel solid micro-gyroscope［C］∥Proc of 19th IEEE Conf on MEMS，Turkey，2006:634－637.

［2］ Xu Yuanjie，Lee J E Y.Does greater piezo-resistive transduction give rise to higher anchor loss in a square-extensional mode micromechanical resonator［J］.Sensors and Actuators A:Physical，2013，202:111－117.

［3］ Sorenson L，Fu J，Ayazi F.Linear acoustic bandgap arrays for spurious mode suppression in piezoelectric MEMS resonators［C］∥Proc of 65th IEEE International Frequency Control Symposium，San Fransisco，2011:1－5.

［4］ Harrington B P，Abdolvand R.Q-enhancement theory minimization of acoustic radiation in micromachined lateral-mode resonators［C］∥Proc of 15th IEEE Conf on Solid-State Sensors，Actuators and Microsystems(Transducers)，Denver，CO，2009:700－703.

［5］ Lin C M，Lai Y J，Yen T T，et al.Quality factor enhancement in lamb wave resonator utilizing ALN plates with convex edges［C］∥Proc of 15th IEEE Conf on Solid-State Sensors，Actuators and Microsystems(Transducers)，Beijing，2011:1512－1515.

［6］ Wu Xiaosheng，Chen Wenyuan，Zhang Weiping，et al.Modeling analysis of piezoelectric micromachined modal gyroscope(PMMG)［C］∥Proc of 4th IEEE Conf on Nano/Micro Engineered and Molecular Systems，Shenzhen，2009:304－309.