结合三次样条插值函数的地铁地表沉降监测预报模型

苏超威，丁克良，2，周命端，2，刘 淼

(1．北京建筑大学测绘与城市空间信息学院，北京100044;2．现代城市测绘国家测绘地理信息局重点实验室，北京100044)

一、引 言

地表沉降监测是地铁变形监测中一项重要的监测内容，其目的是为了保障地铁施工及运营管理的安全，通过沉降监测发现沉降异常和安全隐患［1］。鉴于地铁地表沉降监测干扰因素多，安全隐患大，应严格按照规范测量。沉降监测过程中，单次测量一般不超限，符合测量规范，然而随着时间的增加，变形速率的不确定性导致累计沉降量可能变化很大，容易出现突发事故，因此，必须要做好地表沉降监测工作，对沉降趋势进行数据预报，为安全施工提供数据支撑。

本文针对某地铁工程在施工期间进行地表沉降监测，采用拓普康DL-501电子水准仪进行二等水准测量，经内业平差处理获得了多天的实测数据资料，运用Matlab语言编写三次样条插值函数拟合外推预测程序，并针对观测数据量和时间间隔两种因素建立了两种不同的预测模型，对比分析插值拟合和外推预测的精度。

二、三次样条插值函数原理

三次样条插值函数是最常用的插值曲线拟合函数，其良好的收敛性、可靠的稳定性以及具有二阶光滑度等优点使其在函数逼近、微积分和微分方程等科学计算中应用广泛，在工程数据处理中也起到非常重要的作用。

若函数S(x)∈C2[ a，b]，且在每个小区 间[ xj，xj+1]上是三次多项式，其中a=x0＜x1＜x2＜…＜xn=b是给定节点，则称S(x)是节点x0，x1，x2，…，xn上的三次样条函数。若在节点xj上给定函数值yj=f(xi)(j=0，1，…，n)，并成立S(xj)=yj(j=0，1，2，…，n)，则称S(x)为三次样条插值函数［3-6］。

常见的三次样条插值函数边界条件有3种情况［3-6］

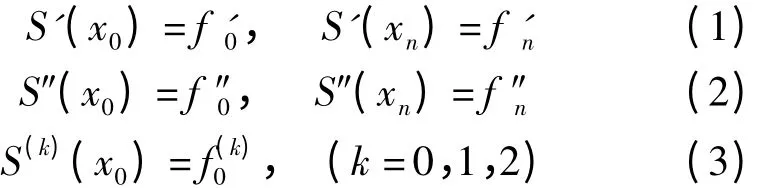
三、应用实例

为分析三次样条插值函数应用于地铁地表沉降监测的预报精度情况，利用某地铁沿线地表沉降监测某M点的部分实测观测资料为例，运用Matlab编程，分别从相同时间间隔且不同观测数据量和相同观测数据量且不同时间间隔两种情况建立3种不同的沉降监测预测预报模型［7-9］，并进行对比分析。某M点的部分实测沉降观测数据见表1。

表1 某M点的沉降监测数据资料

为分析相同时间间隔、不同观测数据量构建的预测预报模型在地表沉降监测预报中内插与外推的预测精度及效果，本文采用时间间隔为5天、观测数据量分别为30天和60天的沉降观测资料建立两种不同的预报模型(依次简记为预测预报模型一和预测预报模型二)，利用三次样条插值函数方法对沉降量进行预测预报。

预测预报模型一:当采用时间间隔为5天，且观测数据量具有30天的沉降观测数据建立预测预报模型时，内插第23天M点的地表沉降量以及外推第2天和第4天(即第32天和第34天)M点的地表沉降量，将获得的第23天及第32天和第34天的地表预测沉降量分别与其对应的实测观测数据进行对比分析。

建立的Matlab预测预报模型一代码如下:

t=［0，5，10，15，20，25，30］;

H=［0，2．200，7．016，6．963，1．237，－4．721，－10．415］;

New_t=0:5:35;

New_H=spline(t，H，New_t);

plot(t，H，'－－o'，New_t，New_H);

应用Matlab编程建立的预测预报模型一运行结果如图1所示，其中，内插第85天和外推第5天(即第155天)M点地表预测沉降量与实测观测数据对比分析结果见表2所示。

表2 间隔10天、累计观测30天的预测值与实测值对比

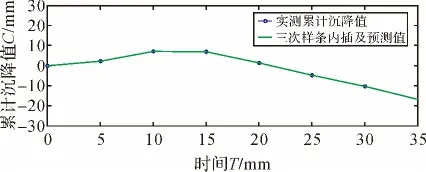
图1 间隔5天、累计观测30天的预测预报模型一运行结果

预测预报模型二:当采用时间间隔为5天，且观测数据量具有60天的沉降观测数据建立预测预报模型时，内插第23天M点的地表沉降量以及外推第2天和第4天(即第62天和第64天)M点的地表沉降量，将获得的第23天及第62天和第64天的地表预测沉降量分别与其对应的实测观测数据进行对比分析。

建立的Matlab预测预报模型二代码如下:

t=［0，5，10，15，20，25，30，35，40，45，50，55，60］;

H=［0，2．200，7．016，6．963，1．237，－4．721，－10．415，－14．463，－17．691，－19．544，－21．383，－23．372，－24．819］;

New_t=0:5:65;

New_H=spline(t，H，New_t);

plot(t，H，'－－o'，New_t，New_H);

应用Matlab语言编程建立的预测预报模型二运行结果如图2所示，其中，内插第23天和外推第2天和第4天(即第62天和第64天)M点地表预测沉降量与实测观测数据对比分析结果见表3。

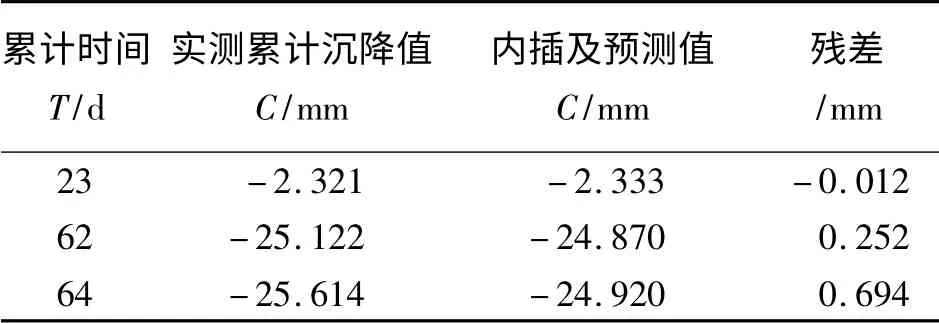
表3 间隔5天、累计观测60天的预测值与实测值对比

图2 间隔5天、累计观测60天的预测预报模型二运行结果

对比表2和表3中的残差量可以看出，当采用相同时间间隔(d=5天)、不同观测数据量(dd=30天和60天)所建立的预测预报模型一和预测预报模型二分别进行内插拟合及外推预测预报时，不论是针对第23天的内插拟合精度测还是针对外推第2天和第4天的预报效果，预报预测模型二略优于预测预报模型一。

在对比分析预测预报模型一与预测预报模型二的内插拟合精度和外推预报效果的基础上，为分析不同时间间隔、相同观测数据量构建的预测预报模型在地表沉降监测预报中内插与外推的预测精度及效果，本文采用时间间隔为10天、观测数据量为60天的沉降观测资料建立预测预报模型，利用三次样条插值函数方法对沉降量进行预测预报，便于与预测预报模型二进行比对分析。

预测预报模型三:当采用时间间隔为10天且观测数据量具有60天的沉降观测数据建立预测预报模型时，内插第23天M点的地表沉降量以及外推第2天和第4天(即第62天和第64天)M点的地表沉降量，将获得的第23天、第62天和第64天的地表预测沉降量分别与其对应的实测观测数据进行对比分析。

建立的Matlab预测预报模型三代码如下:

t=［0，10，20，30，40，50，60］;

H=［0，7．016，1．237，－10．415，－17．691，－21．383，－24．819］;

New_t=0:10:65;

New_H=spline(t，H，New_t);

plot(t，H，'－－o'，New_t，New_H);

应用Matlab语言编程建立的预测预报模型三运行结果如图3所示，其中，内插第23天和外推第2天和第4天(即第62天和64天)M点地表预测沉降量与实测观测数据对比分析结果见表4。

对比表3和表4中的残差量可以看出，当采用相同观测数据量(dd=60天)、不同时间间隔(d=5天和10天)所建立的预测预报模型进行内插拟合及外推预测预报时，不论是针对第23天的内插拟合精度测还是针对外推第2天和第4天的预报效果，预报预测模型二略优于预测预报模型三。

表4 间隔10天、累计观测60天的预测值与实测值对比

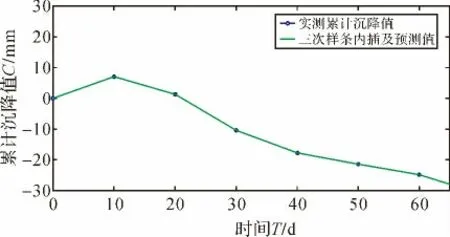
图3 间隔10天、累计观测60天的预测预报模型运行结果

为综合比对分析顾及观测数据量和时间间隔两种因素所构建的3种不同的预测预报模型的内插拟合精度和外推预报效果，将3种模型的内插拟合和外推预报结果与实测值之比较的残差量分析如图4所示。

从图4可以看出，3种模型在内插拟合精度上均优于外推预报精度;3种模型无论是从内插拟合精度上还是外推预报效果上可以看出，模型二为略优;另外，从外推预报残差量的比较分析可发现，外推2天的预报精度效果略高于外推第4天的。

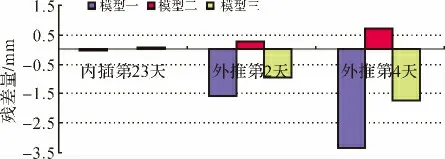
图4 3种模型预测预报结果与实测值之残差量比较分析

四、结束语

本文利用三次样条插值函数，基于Matlab编程建立了3种不同的预测预报模型，以某地铁地表沉降监测特征点M为例进行累计沉降数据预测预报分析，分别从相同时间间隔且不同观测数据量的内插拟合与外推预测、相同观测数据量且不同时间间隔的内插拟合与外推预测两种情况建立了3种不同的预测预报模型并作了对比分析。应用实例表明:3种不同的预测预报模型在内插拟合精度上均优于外推预报精度;3种模型无论是从内插拟合精度上还是外推预报效果上可以看出，具有短时间间隔且长时间累积观测数据所建立的预测预报模型(如模型二)为略优;另外，从外推预报残差量的比较分析可表明，外推天数短的预报精度效果略高于外推天数长的。

［1］ 岳建平，田林亚．变形监测技术与应用［M］．北京:国防工业出版社，2010:16-17．

［2］ 李庆扬，王能超，易大义．数值分析［M］．北京:清华大学出版社，2008:41-46．

［3］ 封建湖，车刚明，聂玉峰．数值分析原理［M］．北京:科学出版社，2001．

［4］ 孟大志，刘伟．现代科学与工程计算［M］．北京:高等教育出版社，2009:32-38．

［5］ 孙祥畅，栾元重，颜世英，等．曲线拟合与插值模型在矿区变形预测中的应用［J］．有色金属(矿山部分)，2012，64(1):2-4．

［6］ 王义峰，刘立龙，文鸿雁．最小二乘曲线拟合在变形监测中的应用［J］．地理空间信息，2007，5(3):109-110．

［7］ 吕喜明，李明远．最小二乘曲线拟合的Matlab实现［J］．内蒙古民族大学学报:自然科学版，2009，24(2):125-127．

［8］ 崔晓东，兰孝奇，张兵良．建筑物沉降规律的综合时序分析［J］．现代测绘，2004，27(1):36-38．

［9］ 丁克良，欧吉坤，赵春梅．正交最小二乘曲线拟合法［J］．测绘科学，2007，32(3):18-19．

［10］穆尔．MATLAB实用教程(第二版)［M］．高会生，刘童娜，李聪聪，译．北京:电子工业出版社，2010:350-352．