GPS控制网坐标转换模型的研究

金俭俭，董彦锋，王 茹，徐录铸，王维宇

(东南大学交通学院，江苏 南京211189)

一、引 言

近些年来，GPS定位技术已广泛用于控制测量等领域。GPS定位的成果属于WGS-84大地坐标系，但我国目前应用的地形图却属于1954北京坐标系或者1980国家坐标系，而不同的坐标系之间存在着平移和旋转关系，因此应用GPS定位成果需要进行坐标转换。我国的平面和高程两个控制系统分别属于不同的系统基准和坐标框架，故随着控制测量区域面积的不同，3个坐标的变化规律呈现出复杂性，如较小区域的控制测量，为了减少长度变形，一般采用无须投影计算的平面直角坐标系统等，而在空间坐标转换问题上需要考虑这些因素。

空间坐标转换模型主要有布尔萨(Bursa)模型、莫洛金斯基(Molodensky)模型、范士模型和武测模型等。上述模型都包括3个平移参数，3个旋转参数和1个尺度参数，因而称为七参数转换模型，本文就布尔萨模型在一定区域GPS控制测量中坐标向高斯直角坐标系的转换进行探讨，并在相同原理基础上将其演变成九参数模型，以解决单一尺度不足问题。

二、坐标系相互转换

1．空间直角坐标系统

如图1所示，两个空间直角坐标系之间存在3个平移量，对应的坐标轴之间存在3个微小的旋转角，及两坐标系之间的尺度比。

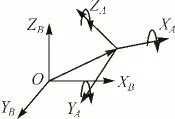
图1 空间直角坐标系

2．布尔萨七参数转换模型

式中，B为1980西安坐标系坐标，A为WGS-84坐标系坐标。

其中3个旋转参数为

在小区域GPS控制测量中，考虑到旋转角都是微小量，对同一点，有式(3)

对式(3)进行整理变换，可得式(4)

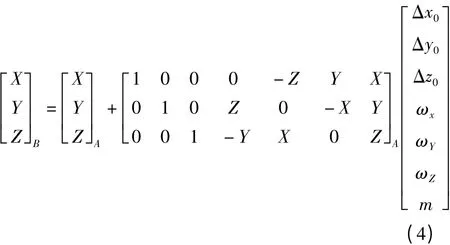
3．间接平差模型

依据式(4)，若求七参数，只要有足够多的重复点观测，就可依据平差理论建立模型。这里按照间接平差模型V=Bδ^X－L建立相关的坐标转换模型，在最小二乘原则下求解七参数。

式中，B矩阵中相关的坐标系数是WGS-84坐标系测得的数据坐标。

4．平差计算及精度评定

由于七参数转换模型中有7个未知数，依据平差原理，需要至少进行坐标联测3个点，每个点分别有x、y、z坐标数据。

设在一控制测量区域已经存在3个坐标点，其1980西安坐标系的坐标已知，然后利用GPS接收机联测这3个点的坐标，得到WGS-84坐标系的坐标，分别为:( x1，y1，z1)，( x2，y2，z2)，( x3，y3，z3)，将其代入，可得B矩阵。这里3个点坐标测量的精度相同，可设其权阵为单位阵。依据最小二乘法原理VTPV=min可得

由此可以计算出七参数转换模型中的7个参数，代入式(6)可以得到任意一点1980坐标系中的坐标。

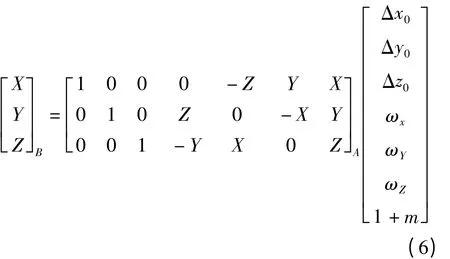
由此，两个坐标系之间坐标转换的模型就建立了。求出转换参数后，依据转换模型可求出公共点在新坐标系下的坐标，依据V=Bδ^X－L可得残差矩阵，而综合变换法的原理就是对转换后的残差矩阵进行拟合。拟合是从数学原理来对数据的分析预估，可采用多项式拟合及曲面拟合等多种拟合方法，其中以最小多项式拟合最为常用。在实际应用中，更为重要的是对各种模型的比较，以便选择一个最优模型，这里选用单位权方差估值的计算式作为拟合模型的选取准则。即

式中，n表示参加拟合计算的数值个数，t为拟合模型的参数个数。

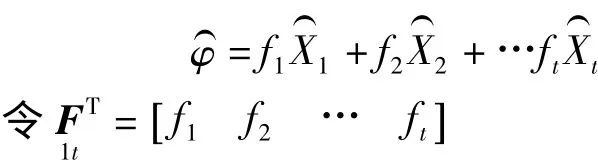
由协因数传播定律知Q)x)x=(BTPB)－1

故 Q)φ)φ=FTQ)x)xF

5．九参数坐标转换模型

传统的七参数坐标转换模型是单尺度模型，因此只需解算一个尺度参数即可。然而，GPS控制测量观测的成果有高程方向上的误差和平面坐标方向上的误差，分别属于两个基准系统的数据，故尺度比并无可比性。因此GPS坐标转换如果仍以单尺度模型进行坐标转换，则不能很好地反映出两坐标系统尺度上的差异。

因而将七参数转换模型中尺度参数进行延伸，在X、Y、Z轴上各设置一个尺度参数是比较合理的，

这样就得到九参数坐标转换模型。

其中三尺度模型可表示为

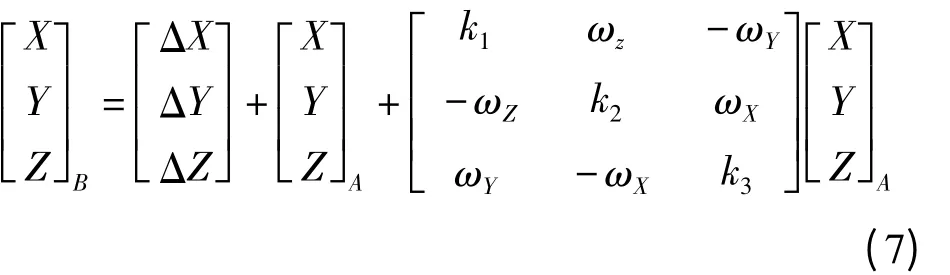
将其写成误差方程为

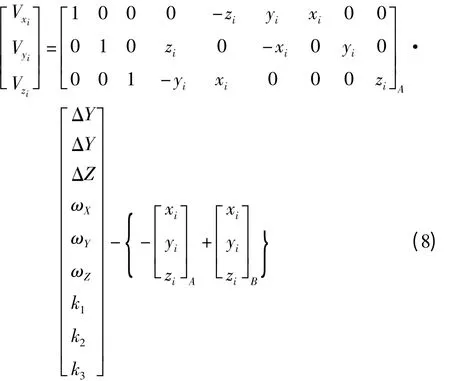
根据误差方程式，按最小二乘法原理，即可求出两坐标系之间的九转换参数及坐标转换精度。具有3个尺度参数的九参数模型其精度要比七参数模型的精度要高，更适用于小区域的GPS控制网的坐标转换。

三、实例分析

如某测区面积约50 000 km2，5个已知重合点坐标见表1，分别为WGS-84和北京54坐标系下的坐标，依据上面建立的布尔萨模型及其延伸，求出相关的转换模型，对两种模型的精度进行比较(见表1)。

1．七参数坐标转换模型

观测数n=15，必要观测数t=7，体系的自由度为15－7=8。

将表1中各点数据代入七参数的误差方程中，依据δx=(BTPB)－1BTPL，(这里的权阵为单位阵)可求解出

式中，Δx0、Δy0、Δz0单位为m;ωΧ、ωY、ωZ单位为s。

表1 两种模型精度比较

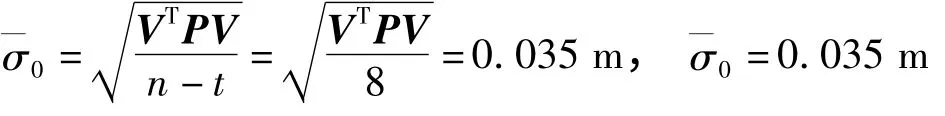
2．九参数坐标转换模型

观测数n=15，必要观测数t=9，体系的自由度为15－9=6。

将表中各点数据代入九参数的误差方程中，依据δx=(BTPB)－1BTPL，(这里的权阵为单位阵)可求解出

通过两种模型精度的比较，可以看出九参数模型的单位权中误差要小于七参数模型的单位权中误差，由此，在小区域的GPS控制网中，采用九参数坐标转换模型可以提高精度，减小误差，且更适用于高差变化大的区域。针对控制测量面积的不同，其已知重合点的均匀性和密度应有不同的要求，如对于小区域的控制测量来说可宽松一些。

四、结束语

本文对一定区域GPS控制网的坐标转换进行了研究，并结合布尔萨空间坐标转换模型的原理及特点，将七参数坐标转换模型进行了延伸，在相同原理的基础上，演变成九参数坐标转换模型，弥补了七参数坐标转换模型中单一尺度的不足。研究成果对于测绘生产具有实际的应用价值和意义。

［1］ 李成仁，岳东杰，袁豹，等．基于最小二乘配置的九参数模型在三维坐标转换中的应用［J］．测绘与空间地理信息，2014，37(7):193-196．

［2］ 徐仕琪，张晓帆，周可法，等．关于利用七参数法进行WGS-84和BJ-54坐标转换问题的探讨［J］，测绘与空间地理信息，2007，30(5):33-42．

［3］ 孙小荣，张书毕，徐爱功，等．七参数坐标转换模型的适用性分析［J］．测绘科学，2012，37(6):37-39．

［4］ 武汉大学测绘学院测量平差学科组．误差理论与测量平差基础［M］．武汉:武汉大学出版社，2014．5．