2014年陕西省高考理科数学第21题研究

汪仁林+姚利娟

最近，在研究陕西省高考理科压轴题时，有了意外的收获，得到了标准答案以外且优于标准答案的新解法，汇总如下，与读者共享.

题目 （2014年陕西高考理科数学第21题）

设函数f（x）=ln（1+x），g（x）=xf′（x），x≥0，其中f′（x）是f（x）的导函数.

（Ⅰ）令g1（x）=g（x），gn+1（x）=g（gn（x）），n∈N+，求gn（x）的表达式;

（Ⅱ）若f（x）≥ag（x）恒成立，求实数a的取值范围;

（Ⅲ）设n∈N+，比较g（1）+g（2）+…+g（n）与n-f（n）的大小，并加以证明.

解析 （Ⅰ）由题知，g1（x）=g（x）=x1+x，gn+1（x）=g（gn（x））=gn（x）1+gn（x），所以1gn+1（x）=1+gn（x）gn（x）=1+1gn（x），令bn=1gn（x），则数列{bn}是以b1=1g1（x）=1+xx为首项，以1为公差的等差数列，所以bn=1+xx+（n-1）×1=1+nxx，即1gn（x）=1+nxx，所以gn（x）的表达式为：gn（x）=x1+nx.

评析 此种解法太经典了，将问题转化为由数列递推公式求通项公式，而考题标准答案所给解法为先通过归纳推理猜想出gn（x）的表达式，然后用数学归纳法证明，与此解法相比就显得复杂了.

（Ⅱ）已知f（x）≥ag（x）恒成立，即ln（1+x）≥ax1+x （*）恒成立.①当x=0时（*）式显然恒成立，此时a∈R;②当x>0时，x1+x>0（*）式可化为a≤1+xln（1+x）x，设φ（x）=1+xln（1+x）x（x>0），则a≤φ（x）min，φ′（x）=x-ln（1+x）x2，令h（x）=x-ln（1+x）（x>0），则φ′（x）与h（x）同号.因为h′（x）=x1+x>0，所以函数h（x）在（0，+∞）上为增函数，所以h（x）>h（0）=0，所以φ′（x）>0，所以函数φ（x）在（0，+∞）上为增函数，所以

φ（x）min→φ（0）=limx→0（1+x）ln（1+x）x=

limx→0[（1+x）ln（1+x）]′（x）′

=limx→0ln（1+x）+11=1（洛必达法则），所以此时a≤1.因为（*）式对x≥0恒成立，所以①②所求a的范围求交集即可，所以实数a的取值范围是（-∞，1].

评析 此种解法关键是分离参数，把问题转化为不含参数的函数通过多次求导来求最值，然后利用洛必达法则可轻松获解.当然，解题过程中的一些细节问题的处理应引起重视.对比考题所给标准答案可知，此种方法思路非常清晰，学生更容易掌握！值得提倡.

（Ⅲ）由题设知：g（1）+g（2）+…+g（n）=12+23+…+nn+1，n-f（n）=n-ln（n+1），当n=1时，g（1）+g（2）+…+g（n）=g（1）=12，n-f（n）=1-ln（1+1）=lne2<lne=12，由此猜想g（1）+g（2）+…+g（n）>n-ln（n+1）.此不等式等价于12+13+…+1n+1<ln（n+1）.证明如下：

证法1 （数学归纳法）12+13+…+1n+1<ln（n+1）.

①当n=1时，12<ln2显然成立.②假设n=k（k≥1）时，有12+13+…+1k+1<ln（k+1）成立.那么n=k+1时，有12+13+…+1k+1+1k+2<ln（k+1）+1k+2.要证n=k+1时也成立，只需证ln（k+1）+1k+2<ln（k+1+1），即证lnk+2k+1>1k+2，在（Ⅱ）中，取a=1可得ln（x+1）>x1+x，令x=1k+1，则lnk+2k+1>1k+2，这就说明当n=k+1时也成立.综上①②可知结论对n∈N+成立.

证法2 由（ln（x+1））′=1x+1，∫n+111xdx=lnxn+1

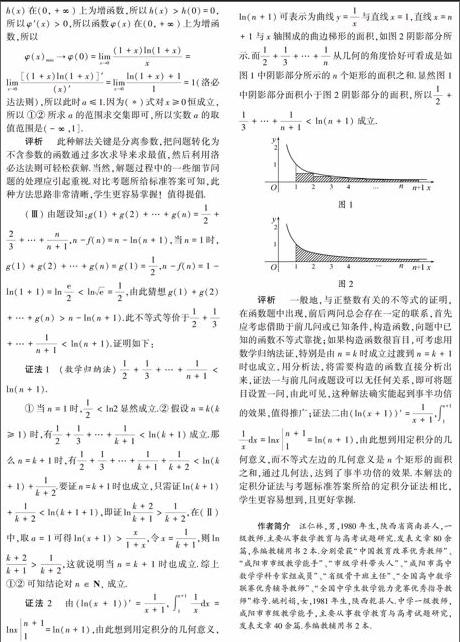
1=ln（n+1），由此想到用定积分的几何意义，ln（n+1）可表示为曲线y=1x与直线x=1，直线x=n+1与x轴围成的曲边梯形的面积，如图2阴影部分所示.而12+13+…+1n从几何的角度恰好可看成是如图1中阴影部分所示的n个矩形的面积之和.显然图1中阴影部分面积小于图2阴影部分的面积，所以12+13+…+1n+1<ln（n+1）成立.

图1图2

评析 一般地，与正整数有关的不等式的证明，在函数题中出现，前后两问总会存在一定的联系，首先应考虑借助于前几问或已知条件，构造函数，向题中已知的函数不等式靠拢;如果构造函数很盲目，可考虑用数学归纳法证，特别是由n=k时成立过渡到n=k+1时也成立，用分析法，将需要构造的函数直接分析出来，证法一与前几问或题设可以无任何关系，即可将题目设置一问，由此可见，这种解法确实能起到事半功倍的效果，值得推广;证法二由（ln（x+1））′=1x+1，∫n+111xdx=lnxn+1

1=ln（n+1），由此想到用定积分的几何意义，而不等式左边的几何意义是n个矩形的面积之和，通过几何法，达到了事半功倍的效果.本解法的定积分证法与考题标准答案所给的定积分证法相比，学生更容易想到，且更好掌握.

作者简介 汪仁林，男，1980年生，陕西省商南县人，一级教师.主要从事数学教育与高考试题研究.发表文章80余篇，参编教辅用书2本.分别荣获“中国教育改革优秀教师”、“咸阳市市级教学能手”、“市级学科带头人”、“咸阳市高中数学学科专家组成员”、“省级骨干班主任”、“全国高中数学联赛优秀辅导教师”、“全国中学生数学能力竞赛优秀指导教师”称号.姚利娟，女，1981年生，陕西乾县人.中学一级教师，咸阳市市级教学能手，主要从事数学教育与高考试题研究，发表文章40余篇.参编教辅用书2本.