湍流大气中动态激光散斑的数值模拟

韩星星

(西安交通大学城市学院，陕西 西安710018)

1 引言

利用目标激光散斑特征对目标的运动特征进行检测在军事和民用领域具有重要的应用价值。自20世纪80年代以来，国内外大批学者对漫射平面、圆柱、圆锥、球等多种目标平动、转动以及振动状态下的散斑特性进行了大量的理论和实验研究［1－2］。随着计算机技术的发展，数值模拟逐渐成为一种重要的研究手段，2004年李小兵等人提出了利用激光散斑实时测量目标散射面角振动的原理，并从干涉条纹的角度对仿真参数进行了分析，模拟了两个散射元的情况［3］。但是这种模拟方法由于效率太低而无法用于大量散射元情况。1999年程传福等人对高斯随机表面光散射产生的散斑场进行了模拟并分析了散斑光强的概率密度函数［4］，但是该算法只适用于夫琅和费区。

在实际应用中，激光的发射和接收通常都是在大气环境下进行的，受到大气湍流的影响，激光会发生闪烁、漂移、展宽等现象。这些现象对目标回波散斑特征产生不可忽视的影响。经过几十年的研究，人们已经发展出了几何光学、Rytov近似、Markov近似等解析方法来计算激光的传输特性，但它们都是在一定条件下的近似，其适用范围有限。而数值方法由于其广泛的适应性得到众多研究者的重视，其中研究最多的是分步傅里叶方法。

分步傅里叶方法是求解抛物方程的一种通用的方法，在多个领域都有应用。从20世纪80年代开始，国内外学者就不断地把分步傅里叶方法应用到光波在大气中的传输计算中［5－8］，但多数文献模拟的都是静止光斑，无法体现光斑随时间的变化特性。本文首先在无湍流的情况下利用分步傅里叶算法，模拟了真空中的动态散斑场，然后结合冻结场理论，模拟了湍流大气中的动态散斑场，并分析了两种情况下激光回波散斑场的时空相关特性。

2 分步傅利叶算法的推导

在图1所示的系统中，激光器发射孔径位于平面z=0上，光轴与z轴平行，接收器位于平面z=L，s和ρ分别是发射平面和接收平面上垂直于传播轴的位置矢量。在发射平面上，单位振幅高斯波束的光场为:

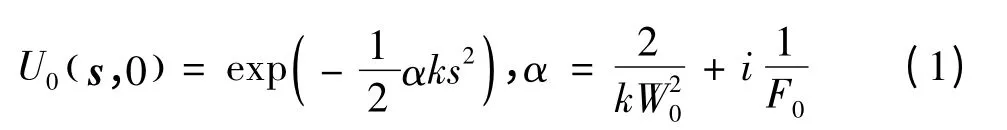
其中，k是波数;W0是波束有效半径;F0是波前曲率半径。

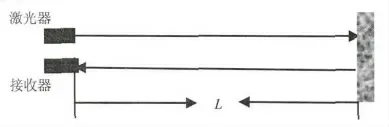
图1 激光散斑测量示意图

分步傅里叶算法是一种在电磁波及光波传输模拟领域广泛应用的方法，算法原理公式［9］为:

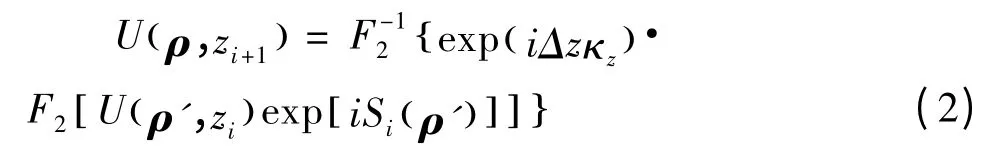
为了利用数值方法计算式，其中的U和S都要经过离散化［10－11］:

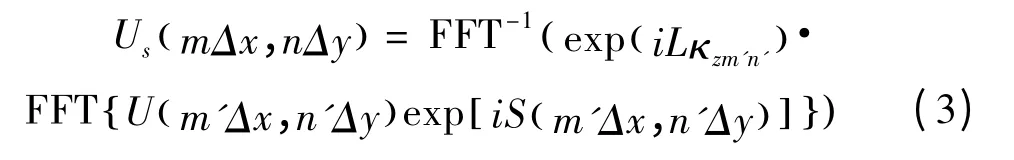
把相位屏划分为N×N的正方形网格，场和相位屏只在网格结点上有值。当激光在真空中传播并被漫射面反射时，其模拟过程只需要一个相位屏，这个相位屏代表了漫反射面，其生成方法为:

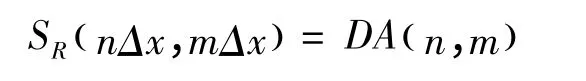
其中，D是相位屏的均方差;A是独立均匀分布的随机数矩阵。

为了考察散斑的动态特征，需要模拟当物体运动时，不同时刻的散斑图样。式(3)可变形为:

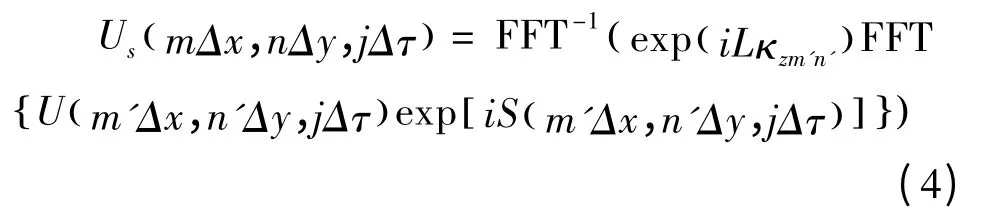
假设目标以速度v沿x轴正向平动，则相位屏也要做相同的运动，即:

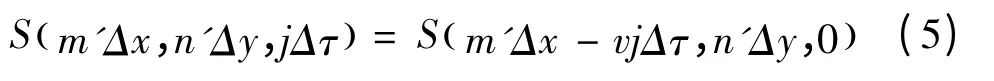
如果l=vnΔτ/Δx是整数，则在模拟第j个散斑时，直接把矩阵S沿x轴正向移动l个网格，空出来的网格点用新生成的随机数补上即可。但是在一般情况下，l不是整数，而漫射面的性质决定了不能用插值方法得到任意位置的S。本文采用沿相反方向移动光源的方法，对于第n个散斑，发射波束为:

3 真空中散斑的模拟

选择发射波为准直的高斯波束，波长λ=1．06μm，初始半径W0=3 cm，半径为WR=3 cm的漫射圆盘距离波源L=2000 m，目标以v=2 m/s的速度沿x方向移动，单站接收。不考虑大气湍流对激光的扰动，图2给出了不同时刻接收面上的散斑图样。

可以看到相邻时刻的两幅图都有较强的相似性，时间间隔越大，散斑图样相差也越大。随着时间的推移，亮斑的位置发生的移动，且形状发生了变化，有的亮斑消失了，并有新的亮斑生成，即通过模拟图像观察到了动态散斑现象中的平移和沸腾现象。

利用模拟得到的散斑可以统计计算散斑场的空间相关函数，它反映了散斑场随着横向位置移动的变化快慢，决定了散斑颗粒的尺寸。图3给出了当初始半径不同时，散斑场空间相关函数随着两点距离的变化，它们对独立生成的100个散斑图样进行统计得到的。三条曲线中，当W0=3 cm时激光的散斑场空间相关函数下降最慢，其次是W0=5 cm和W0=1 cm。在真空中当初始半径分别为W0=1，3，5 cm时，照射在目标平面上的光斑半径分别为W=3．8，4．2，5．4 cm，这说明散斑尺寸是由目标平面上的光斑半径决定的，这和理论公式是一致的，即光斑半径越小，散斑尺寸越大。

图2 真空中漫射面回波动态散斑图样

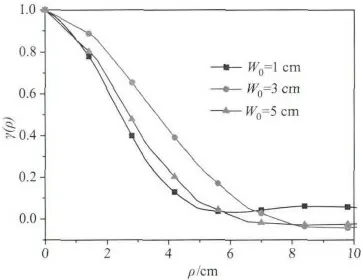
图3 真空中漫射面回波散斑场空间相关函数

利用一系列不同时刻的散斑图样可以统计计算散斑图样相关程度随着时间间隔的变化。图4显示了不同初始半径的激光散斑图样时间相关函数。可以看出时间相关函数的下降速度与目标移动速度成正比。对于不同的初始半径的激光，散斑时间相关函数的下降速度由快到慢依次是W0=1，5，3 cm，这和空间相关函数的变化是不同的。这说明，时间相关函数不但和目标平面上的光斑半径有关，还和目标平面上的光斑相位分布有关。当W0=3 cm时的光斑最小，其散斑最大，相应的相关时间最大。W0=1 cm时的光斑虽然小于W0=5 cm，但是当W0=1 cm时，光斑上的相位变化要更剧烈，从而造成目标移动时，散斑相关时间的减小，所以W0=1 cm时的相关时间最小。

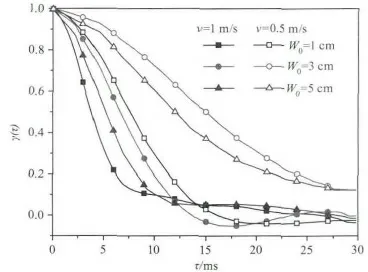
图4 真空中漫射面回波散斑场时间相关函数

4 湍流中的散斑模拟

当传输路径处于湍流之中时，激光在前向传输和反射过程中受湍流的扰动，振幅和相位都会发生变化，形成的散斑场的统计特性也会发生变化。湍流对光场的扰动也可以利用相位屏模拟，但是只有当路径较短，湍流扰动较小时，才可以把整个路径的湍流等效为一个相位屏，对于较长的路径及较强的湍流(σ2I=1．23C2nk7/6L11/6＞0．1)时，把整个路径划分为多段，每个段路径上的湍流都可以等效为一个随机相位屏，第(i+1)个相位屏上的场可以利用式(4)由第i个相位屏上的场得到，以此类推即可由发射场得到散射场。

湍流是由空气运动形成的，所以湍流通常还伴随着一定速度的风，根据冻结场理论，对散斑场时间统计特性有影响的是风的横向速度。假设风的速度矢量为vw=vxex+vyey，其中ex、ey分别是沿x、y方向的单位矢量。在Δτ的时间间隔内，湍流等效相位屏沿x、y方向移动的网格数分别为lx=vxnΔτ/Δx和ly=vynΔτ/Δx。由于湍流折射率谱的能量主要集中在低频，所以其等效相位屏起伏在空间上较为缓慢，当lx和ly不是整数时，平移后的相位屏可以采用插值的方法得到。

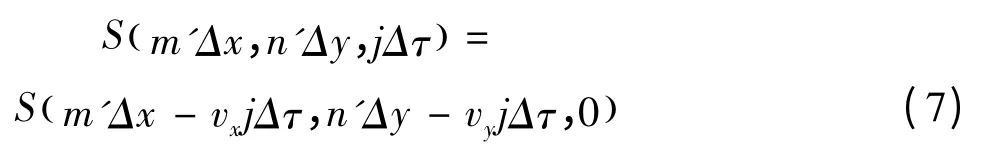
其中，S( m'Δx－vxjΔτ，n'Δy－vyjΔτ，0)可以利用三次样条插值方法由S( m'Δx，n'Δy，0)得到。

当目标运动时，本文采用反向移动整个系统的方法，此时湍流等效相位屏的移动速度应采用v'w= ( vx－v) ex+vyey。在相位屏移动时，必须保证进入有效计算范围内的部分相位屏不能成为空白，所以模拟过程中生成长和宽都为2N的相位屏，当vx－v和vy都为正时，漫射目标的等效相位屏与湍流等效相位屏第一象限重叠，这样可以最大限度的利用生成的相位屏。当v'w为其他值时，依此类推。

在上一节激光散射系统的基础上考虑大气湍流效应，湍流结构常数为C2n=1．8×10－14m－2/3，单程路径上的Rytov方差为σ2I=2，单程路径被平均分为20段，整个路径共设置了40个湍流等效相位屏和一个目标等效相位屏。不考虑前、后向路径上湍流的相关性，即前、后向路径上的相位屏均不相同。

图5给出了湍流大气中不同时刻接收面上的散斑图样，其中目标运动速度为vt=1．0exm/s，风速度矢量vw=－1．0exm/s。相比真空中的散斑，湍流中的散斑样本的不同之处有三点，一是散斑平均尺寸变小了;二是真空中的散斑边缘比较光滑，而湍流中的散斑边缘更加不规则;三是湍流中的散斑随着时间的变化更快，第四幅散斑图和第一幅已经观察不到相似性。

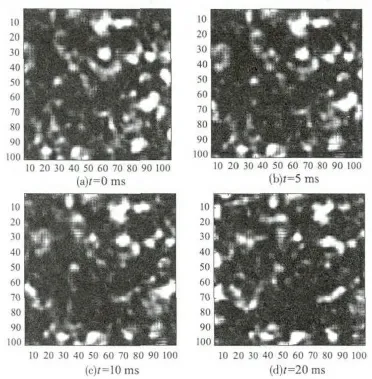
图5 湍流中漫射面回波动态散斑图样

图6 显示了不同初始半径的高斯波束在湍流中照射到无穷大漫射平面形成的散斑场的空间相关函数，它们对独立生成的100个散斑图样进行统计得到的。与图3相比可以发现，在湍流中空间相关函数下降速度更快，这代表着散斑尺寸更小，这与图5显示的信息是一致的。三条曲线下降速度的排序与图3中相同，这表明了湍流对不同初始半径的激光散斑影响大致是相同的。

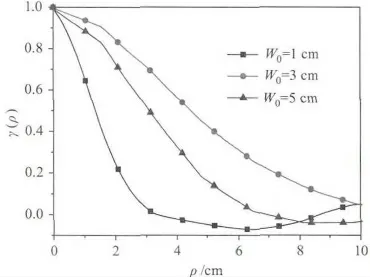
图6 湍流中漫射面回波散斑场空间相关函数

图7 显示了湍流大气中不同初始半径的激光散斑图样时间相关函数。在湍流大气中，即使目标不运动，受湍流效应的影响散斑场仍然随时间变化。当目标运动和风的运动同时存在时，散斑受双重作用调制，时间相关函数下降速度更快，即相关时间变得更小。而风速沿不同方向时，时间相关函数变化不大，说明湍流和目标对散斑场的影响是相互独立的。

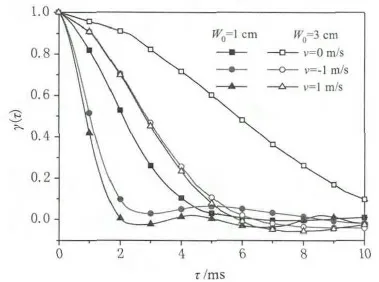
图7 湍流中漫射面回波散斑场空间相关函数

5 讨论与结论

本文采用分步傅里叶算法模拟了真空和湍流大气中激光照射漫射面后，反射波形成的散斑场。并在该方法中引入了时变相位屏，从而模拟了当漫射面运动时以及湍流随着风向运动时，散斑场随着时间的变化。对模拟得到的散斑进统计计算，得到了散斑场的空间和时间相关函数。结果表明，相关长度由目标上的光斑尺寸决定，光斑越大，接收面上的散斑越小。而相关时间不仅受目标平面上的光斑尺寸影响，还受目标平面上的光场相位影响，光场相位随着位置的变化越快，相关时间就越短。本文研究结果为在湍流大气中利用散斑远程测量目标运动速度提供了理论基础。

［1］ A Hayashi，Y Kitagawa．High－resolution rotation－angle measurement of a cylinder using speckle displacement detection［J］．Appl．Opt．1983，22(8):3520－3525．

［2］ QIN Yuwen，DAI Jiabin，CHEN Jinlong．Developments on electronic speckle method［J］．Journal of Experimental Mechanics，1996，11(7):410－416．(in Chinese)秦玉文，戴嘉彬，陈金龙．电子散斑方法的进展［J］．实验力学，1996，11(7):410－416．

［3］ LI Xiaobing，PENG Renjun，WU Jian．Real－time measurement of the object angular vibration by laser speckles［J］．High Power Laser and Particle Beams，2004，16(4):413－416．(in Chinese)李小兵，彭仁军，吴健．目标角振动的散斑法实时测量［J］．强激光与粒子束，2004，16(4):413－416．

［4］ CHENG Chuanfu，QI Dongping，LIU Deli，et al．The computational simulations of the Gaussian correlation random surface and its light－scattering speckle field and the analysis of the intensity probability density［J］．Acta Physica Sinica，1999，48(9):1635－1643．(in Chinese)程传福，亓东平，刘德丽，等．高斯相关随机表面及其光散射散斑场的模拟产生和光强概率分析［J］．物理学报，1999，48(9):1635－1643．

［5］ M Z M Jenu，D H Bebbington．Fourth－moment calculation of optical propagation in a turbulent atmosphere with use of the split－step method．I．Plane wave［J］．J．Opt．Soc．Am．A．，1994，11(11):2862－2870．

［6］ J M Martin，S M Flatte．Intensity images and statistics from numerical simulation of wave propagation in 3－D random media［J］．Applied Optics，1998，27(11):2111－2126．

［7］ RAO Ruizhong．Pattern characteristics of collimated laser beam in a turbulent atmosphere I．Characteristic Radii［J］．Chinese Journal of Lasers，2002，29(10):879－894．(in Chinese)饶瑞中．湍流大气中准直激光束的光斑特征Ⅰ．特征半径［J］．中国激光，2002，29(10):879－894．

［9］ QIAN Xianmei，RAO Ruizhong．Spatial distribution of Gaussian－beam scintillation in atmosphere by numerical simulation［J］．Chinese Journal of Quantum Electronics，2006，23(3):320－324．(in Chinese)钱仙妹，饶瑞中．高斯光束大气闪烁空间分布的数值模拟研究［J］．量子电子学报，2006，23(3):320－324．

［10］WANG Lijin，LI Qiang，WEI Honggang，et al．Numerical simulation and validation of phase screen distorted by atmospheric turbulence［J］．Opto－Electronic Engineering，2007，34(3):1－5．(in Chinese)王立瑾，李强，魏宏刚，等．大气湍流随机相位屏的数值模拟和验证［J］．光学工程，2007，34(3):1－5．

［11］ZHANG Huimin，LI Xinyang．Numerical simulation of wavefront phase sceen distorted by atmospheric turbulence［J］．Opto－Electronic Engineering，2006，33(1):14－19．(in Chinese)张慧敏，李新阳．大气湍流畸变相位屏的数值模拟方法研究［J］．光电工程，2006，33(1):14－19．