强联合大气湍流下到达角起伏时间频率谱分析

都文和，杨婧翾，刘 剑

(1．哈尔滨工业大学，黑龙江 哈尔滨150001;2．齐齐哈尔大学，黑龙江 齐齐哈尔161006)

则小尺度平面波时间频率谱表达式可以写成如下形式:

1 引言

星地激光通信是指以激光束为信息载体进行的卫星与地面站之间的通信。与传统的卫星微波通信技术相比，星地激光通信技术具有速率高、容量大、体积小、质量轻、低功耗、保密性好等优点［1－2］，在民用和军用领域都有广泛的应用前景，是国内外卫星通信领域的研究热点。对于星地链路而言，承载着信息的激光在大气层中传播，并且占用了部分通信信道，激光束穿过大气层时极易受到大气衰减和湍流效应的影响［3－4］，因此，突破大气湍流的影响仍是星地激光通信需要解决的关键问题。然而，目前国内外学者关于大气湍流对星地激光通信影响的研究多集中在单一的Kolmogorov湍流弱起伏条件下［5－6］，但是越来越多的实验数据和理论研究表明，大气湍流的影响已不完全符合Kolmogorov湍流模型［7］，因此，对于星地链路而言，将整个链路的大气湍流都处理成Kolmogorov湍流已经不再符合星地链路大气湍流的实际情况，根据星地链路大气湍流的实际情况研究大气湍流效应，进而研究大气湍流对星地激光通信的影响也就成为了一个需要亟待解决的问题。因为大气折射率湍流不仅是空间变量的随机函数，而且是关于时间变量的一个随机函数，其振幅和相位的随机变化宏观上表现为到达角起伏、光强闪烁和光束漂移等大气湍流效应，时间频率谱是描述到达角起伏特性的重要参量之一，对星地激光通信的链路分析具有重要意义，所以，有必要针对此参量进行理论研究，推导适用于整个星地激光链路的时间频率表达式。

本文首先根据大气湍流的实际情况，即从地面到6 km的对流层符合Kolmogorov湍流，而6 km以上的平流层符合non－Kolmogorov湍流，建立了强联合大气湍流模型，在对流层幂率值α为常数11/3，振幅因子等于0．033，同样地，在平流层幂率值α满足常数5，振幅因子为0．036［8］。然后推导得出了适用于整个星地上行链路的到达角起伏时间功率谱表达式。最后分析了大尺度湍涡和小尺度湍涡对到达角起伏时间功率谱的不同影响，并对不同接收孔径下大天顶角的到达角起伏时间功率谱的变化规律进行了数值仿真，为星地激光通信链路跟瞄系统的设计、在轨试验及实际应用提供了基本的理论依据和关键技术参数。

2 折射率起伏联合功率谱模型

基于星地链路联合大气湍流模型，研究对流层Kolmogorov湍流和平流层non－Kolmogorov湍流对到达角起伏时间功率谱的联合影响。根据大气湍流的实际情况得出的大气折射谱模Φn(κ，z)有以下形式:

式中，Φn1(κ，z)是从地面到6 km对流层的大气折射谱模型，而Φn2(κ，z)是6 km以上的平流层的大气折射谱模型。κ为空间频率向量，符合Hufnagel－Valley模型［9］:

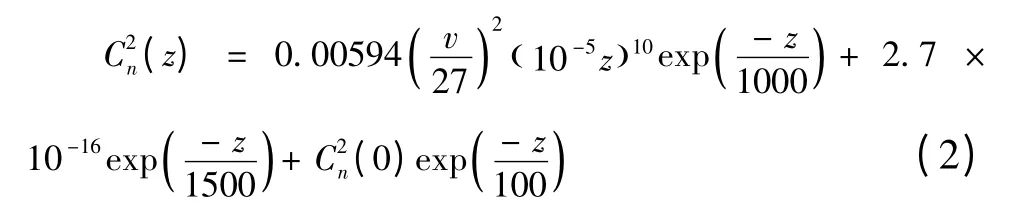
其中，风速v=21 m/s;C2n(0)=1．7×10－14m－2/3;C2n(z)是Kolmogorov湍流大气折射率结构常数，单位是m－2/3。由上述模型可知，大气折射率结构常数是关于高度的变化而变化的函数。

式中，珔C2n(z)是non－Kolmogorov湍流大气折射率结构常数，单位是m－2;C2n0是海拔高度6 km时，Kolmogorov湍流大气折射率结构常数值;HNk是non－Kolmogorov湍流的初始高度，取值6 km;H0是大气标高，取值6 km。

由于大气湍流对到达角起伏的影响可以看作是大尺度湍涡和小尺度湍涡共同作用的结果，因此，根据修正Rytov理论，用符号Gx(κ，α)和Gy(κ，α)分别表示大尺度湍涡和小尺度湍涡引起的空间滤波函数，空间滤波函数的表达式如下［9］:

其中，κx=klx/L是类似于内尺度参量的大尺度折射空间截止频率;κ是光波系数;κy=1/ly是小尺度折射空间截止频率。

对于Kolmogorov湍流模型而言，当幂率α=11/3时，有如下结论:

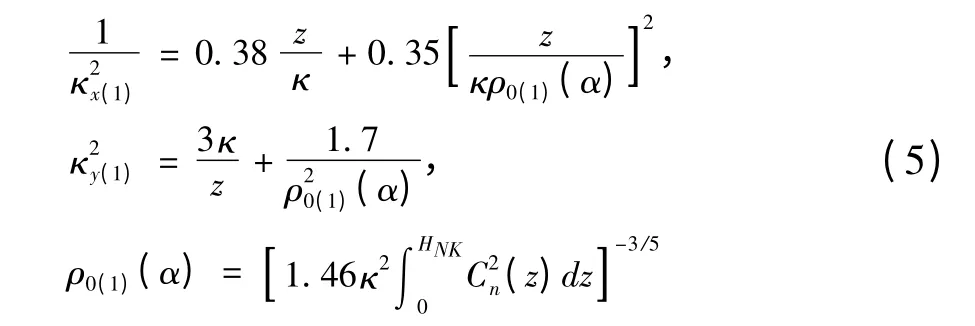
同样，对于non－Kolmogorov湍流模型来说，当幂率α=5时，有如下结论:

3 到达角起伏时间频率谱

由于大气折射率湍流场不仅是空间变量的随机函数，也是时间变量的随机函数，因此大气湍流中的光波起伏也应具有其特定的时间特性。根据泰勒冻结湍流假设Cα(τ，β)=Cα(r－υτ，β)可知，到达角起伏的时间协方差函数表达式为:

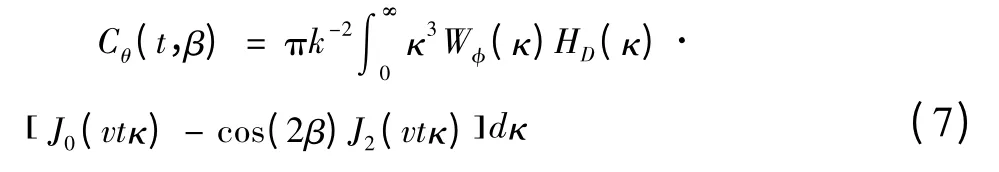
其中，HD(k)是接收圆孔的空间滤波函数;W(κ，β)是空间相位谱;J0(x)和J2(x)分别是零阶和二阶贝塞尔函数。接收圆孔对畸变波前的到达角起伏有平滑作用，此时测量得到的到达角起伏是圆孔内畸变波前的整体到达角起伏。望远镜系统的点扩展函数［10］:

其中，D是接收圆孔直径，常数b=0．4832。

由于到达角起伏时间协方差函数的傅氏变换即为时间频谱，在上行链路中，可以近似的以平面波模型作为研究对象，因此，平面波的相位功率谱为:

将式(1)和式(8)代入式(9)得上行链路平面波的到达角起伏时间功率谱表达式:

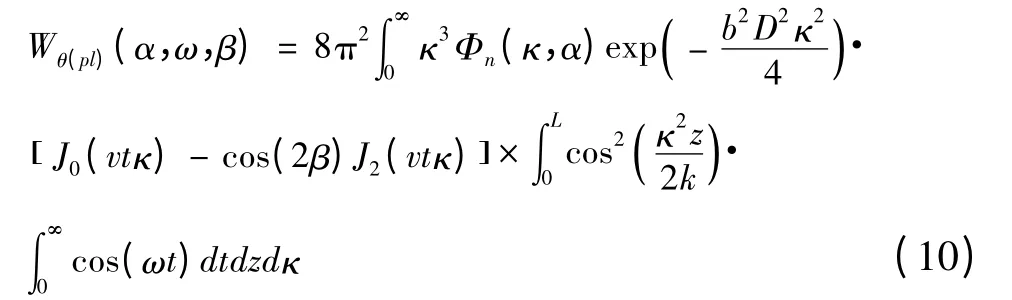
利用积分关系恒等式:

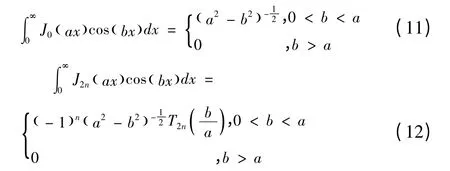
其中，T2n(z)是Tchecichef多项式，其定义式为T2n(z )=cos( 2n cos－1z)。

因此，可以得出平面波到达角起伏时间功率谱表达式如下:

3．1对流层到达角起伏时间功率谱

对流层大气湍流效应符合Kolmogorov湍流模型，将式(1)代入式(13)可得光束在对流层传播的到达角起伏时间功率谱表达式:

可以分别得出大尺度和小尺度平面波到达角起伏时间功率谱表达式如下，其中κx=κx(1)，κy=κy(1)。

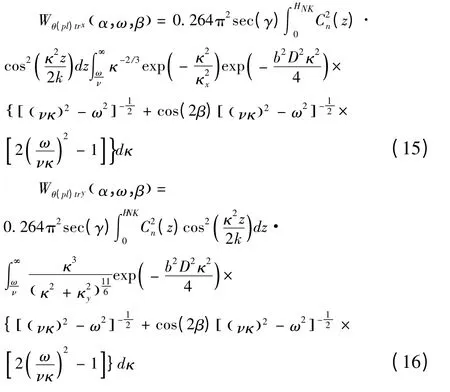
对于大尺度平面波到达角起伏时间功率谱来说，应用以下几何近似方法可得:

将式(17)代入式(15)可得大尺度平面波到达角起伏时间功率谱表达式如下:

根据积分恒等式:

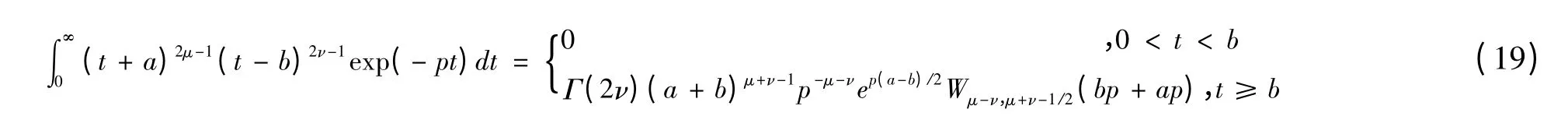
对式(18)进行积分可以得出大尺度平面波时间频率谱解析式如下:

同样的，对于小尺度湍涡存在如下几何光学近似表达式:

则小尺度平面波时间频率谱表达式可以写成如下形式:

运用积分恒等式(19)可以得出以下小尺度平面波时间频率谱表达式:

综上所述，对流层平面波到达角起伏时间功率谱表达式为:

3．2 平流层到达角起伏时间功率谱

平流层大气湍流效应符合non－Kolmogorov湍流模型［11］，将式(1)代入式(13)可得光束在平流层上行链路传播的到达角起伏时间功率谱表达式:

运用相同的几何光学近似法可以分别得出大尺度湍涡和小尺度湍涡在平流层上行链路传播的到达角起伏时间功率谱，其中，κx=κx(2)，κy=κy(2)．

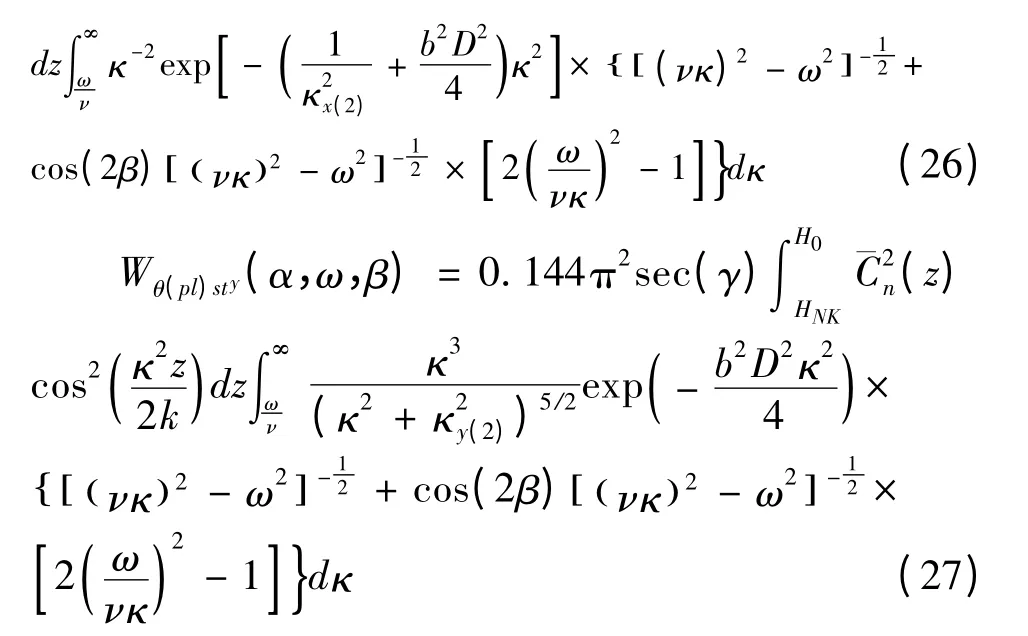
根据积分关系式(19)可以得出大尺度湍涡和小尺度湍涡在平流层上行链路传播的到达角起伏时间功率的表达式:

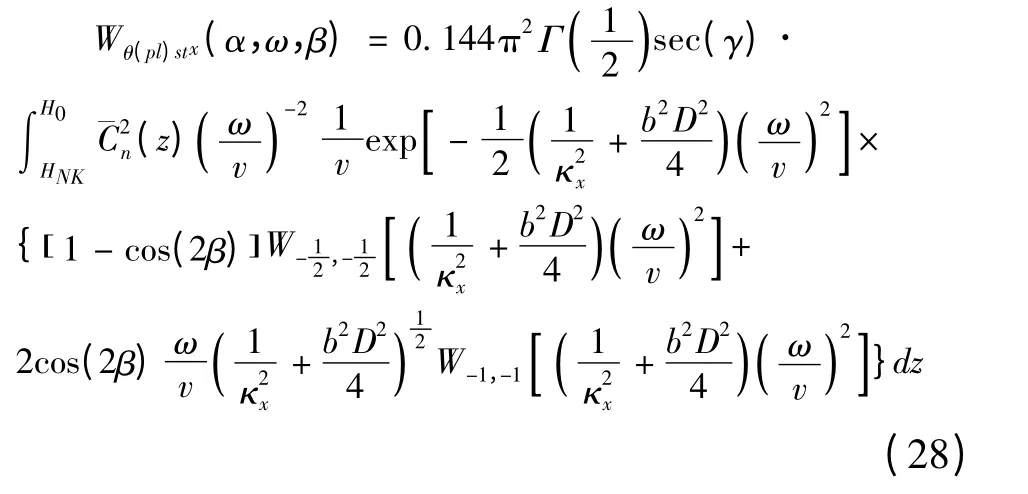
综上所述，平流层平面波到达角起伏时间功率谱表达式为:

4 结果与分析

本文基于上述理论模型，分别将对流层Kolmogorov湍流及平流层non－Kolmogorov湍流条件下接收孔径对到达角起伏时间频率谱的影响进行了数值仿真［12］。分析中，为了使仿真生成的数据更符合大气湍流的实际情况，在强起伏条件下，选取波长λ=1550 nm，风速v=2 m/s，天顶角γ=75°，测量方向β=0°。

图1给出了Kolmogorov大气湍流中不同接收孔径下到达角起伏时间频率谱的变化规律，可以分为低频段和高频段两个区间，两频段分界点的频率大致位于1附近，其中图1(a)对应于大尺度到达角起伏时间频率谱，图1(b)对应于小尺度到达角起伏时间频率谱。从图1(a)中明显看出，大尺度到达角起伏的时间频率谱与接收孔径具有如下规律:对于相同频率，大尺度到达角起伏时间频率谱随接收孔径D的增大而减小;对于相同的接收孔径，大尺度到达角起伏时间频率谱随频率值的增大而减小;低频谱谱线变化较大，而高频谱谱线变化相对较小。从图1(b)中明显看出，小尺度到达角起伏时间频率谱与接收孔径具有如下规律:对于相同频率，小尺度到达角起伏时间频率谱在低频段随接收孔径D的增大而减小，而高频段则相反;对于相同的接收孔径，小尺度到达角起伏时间频率谱随频率值呈现先增大而后减小的趋势。对比图1中的(a)和(b)可以得出，在对流层Kolmogorov大气湍流条件下，小尺度时间频率谱远小于大尺度时间频率谱，因此，在分析对流层Kolmogorov湍流中的到达角起伏时间频率谱变化规律时，可以得到大气湍流对其产生的影响主要是由大尺度湍涡产生的，小尺度湍涡的影响可以忽略。

图2给出了平流层non－Kolmogorov大气湍流中不同接收孔径下到达角起伏时间频率谱的变化规律，其中图2(a)对应于大尺度到达角起伏时间频率谱，图2(b)对应于小尺度到达角起伏时间频率谱。从图2(a)中明显看出，大尺度到达角起伏的时间频率谱与接收孔径具有如下规律:对于相同频率，大尺度到达角起伏时间频率谱随接收孔径D的增大而减小;对于相同的接收孔径，大尺度到达角起伏时间频率谱随频率值的增大而减小;低频谱谱线变化较大，而高频谱谱线变化相对较小。从图2(b)中明显看出，小尺度到达角起伏的时间频率谱与接收孔径具有如下规律:对于相同频率，小尺度到达角起伏时间频率谱与接收孔径的变化规律一致;对于相同接收孔径，低频谱线急剧增加，而高频谱线增加则较为平缓。对比图2中的(a)和(b)可以得出，在平流层non－Kolmogorov大气湍流条件下，可以得出与对流层相似的结论，即大气湍流对到达角起伏时间频率谱产生的影响主要是由大尺度湍涡产生的，小尺度湍涡的影响可以忽略。

图1 Kolmogorov湍流，不同接收孔径D下到达角起伏时间频率谱的变化关系

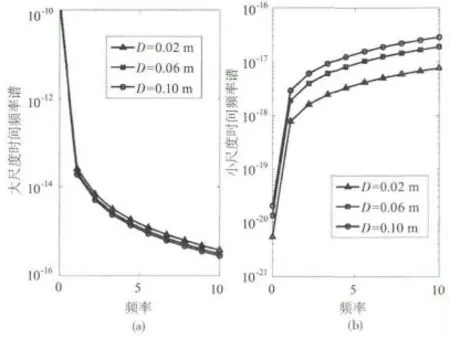
图2 non－Kolmogorov，不同接收孔径D下到达角起伏时间频率谱的变化关系

综合图1和图2中的数据可以得出:在高频段，对流层Kolmogorov湍流到达角起伏时间频率谱大于平流层non－Kolmogorov湍流到达角起伏时间频率谱，即大气湍流对星地链路产生的影响随高度的增加而逐渐减小。

5结论

本文基于修正Rytov近似理论，根据大气湍流的实际情况建立了强联合大气湍流模型，利用谱分析法，得出了中强起伏机制下对流层Kolmogorov湍流及平流层non－Kolmogorov湍流到达角起伏时间频率谱的解析表达式，并利用得到的到达角起伏时间频率谱表达式进行了数值仿真分析，仿真结果表明:对整个星地链路而言，大气湍流对星地链路激光通信产生的影响主要集中在大尺度湍涡上，且在高频段对流层的影响远大于平流层;适当增大接收孔径和频率，可以有效降低大气湍流对星地链路稳定性和可靠性的影响，从而提高星地链路的通信质量。本文研究的内容对星地链路跟瞄系统的性能评估及参数的设计具有一定的参考价值。

［1］ JIANG Xiaofeng，ZHAO Shanghong，ZHAO Yubo，et al．Research on fade characteristic of satellite－to－ground optical communication link subjected to atmospheric［J］．Laser＆Infrared，2011，41(09):965－968．(in Chinese)姜晓峰，赵尚弘，赵宇波，等．星地光通信链路大气湍流衰落特性研究［J］．激光与红外，2011，41(09):965－968．

［2］ L Tan，W Du，J Ma，et al．Log－amplitude variance for a Gaussian－beam wave propagating through non－Kolmogorov turbulence［J］．Optics Express，2010，18(2):451－462．

［3］ W Du，SYu，L Tan，et al．Angle－of－arrival fluctuations for wave propagation through non－Kolmogorov turbulence［J］．Optics Communications，2009，282:705－708．

［4］ WU Lin，YING Jiaju，GENG Biao．Effect of laser propagation in the atmospheric turbulence［J］．Laser＆Infrared，2008，38(10):974－977．(in Chinese)武琳，应家驹，耿彪．大气湍流对激光传输的影响［J］．激光与红外，2008，38(10):974－977．

［5］ L Cui，B Xue，S Zheng，et al．Atmospheric spectral model and theoretical expressions of irradiance scintillation index for optical wave propagating through moderate－tostrong non－Kolmogorov turbulence［J］．Journal of Russian Laser Research，2012，29:1091－1098．

［6］ YUAN Zongheng，ZHANG Wentao．The analysis and research for the laser beam through atmospheric turbulence channel［J］．Laser＆Infrared，2006，36(4):272－274．(in Chinese)袁纵横，张文涛．大气湍流对激光信号传输影响的分析研究［J］．激光与红外，2006，36(4):272－274．

［7］ W Du，F Chen，Z Yao，et al．Influence of non－Kolmogorov turbulence on bit－error rates in laser satellite communications［J］．Journal of Russian Laser Research，2013，34(4):90．

［8］ W Du，H Zhu，D Liu，et al．Effect of non－Kolmogorov turbulence on beam spreading in satellite laser communication［J］．Journal of Russian Laser Research，2012，33:401－408．

［9］ L C Andrews，R L Phillips．Laser beam propagation through random media［J］．SPIE Optical Engineering Press，Bellingham，2005．

［10］H Xu，Z Cui，J Qu．Propagation of elegant Laguerre－Gaussian beam in non－Kolmogorov turbulence［J］．Optics Express，2011，19(22):21163－21173．

［11］H Tang，B Ou，B Luo，et al．Average spreading of a adial Gaussian beam array in non－Kolmogorov turbulence［J］．J．Opt．Soc．Am．A，2011，28(6):1016－1021．

［12］YU Jiping，QI Wenzong，GUO Chunfeng，et al．Numerical simulation of laser propagation through atmospheric turbulence［J］．Laser＆Infrared，2008，38(6):523－527．(in Chinese)于季平，齐文宗，郭春凤，等．激光大气传输特性的数值模拟［J］．激光与红外，2008，38(6):523－527．