崩落法开采岩层移动影响因素的数值模拟

东龙宾 王少泉 金长宇 刘召胜 周 育

(1. 中冶北方工程技术有限公司，辽宁 大连116600;2. 东北大学资源与土木工程学院，辽宁 沈阳110819)

使用崩落法开采引起的岩层移动是一个重大的社会和环境问题，影响顶板大面积冒落的因素众多，机制复杂［1］，难以用确定的试验手段和理论方法解决［2］。国内外学者对于地表沉陷的研究由来已久，如Halbaum 将采空区上方岩层作为悬臂梁，推导出地表应变与曲率半径成反比的理论［3］; 郭增长［4］建立了极不充分开采条件下地表移动的预计方法; 郝冰元［5］分析了开采沉陷预计过程中的相关计算参数的可靠性，对概率积分法预测的参数取值进行了改进;胡斌等［6］通过随随机介质理论，将岩层移动视为一随机过程，对隧道开挖引起的地表沉降进行了研究，黄平路等［7］通过有限元和离散元联合分析的方法，研究了露天于地下联合开采引起的岩层移动规律。离散元法是专门用来解决不连续介质问题的数值模拟方法。20 世纪80 年代中期，王永嘉［8］首次将离散元法引入到国内，该方法特别适用于节理岩体的大变形、大位移分析，并在地表沉降等研究中得到了广泛应用［9-10］。20 世纪80 年代末期，Cundall 等［11］开发了用于模拟节理岩体的三维离散元程序( 3DEC) ，在岩土工程领域得到了广泛应用。本研究基于岩土力学理论，以某大型在建矿山为依托工程，采用离散元程序3DEC，对深部矿体崩落法开采过程中不同因素对岩层移动规律的影响进行分析，研究结论可为深部矿体崩落法开采过程中引起的地表沉陷范围的确定提供一定的参考与指导。

1 计算参数与分析模型的建立

1.1 计算参数的确定

计算参数的准确获取是决定计算结果准确性的前提条件。从国际范围看，岩体工程实践中最常用的峰值强度准则为摩尔－ 库伦强度准则和Hoek －Brown 强度准则，它们分别采用不同的力学关系式描述岩体峰值强度σ1与围压σ3之间的关系。本次计算采用摩尔－库伦强度准则。目前工程实践中在确定摩尔－库伦强度参数值时，多采用了基于Hoek －Brown 强度参数的换算方法。因此，为准确获取现场岩体的力学参数，本研究工作的技术路线如下。

(1) 开展岩石室内试验，获得岩石基本力学参数，如单轴抗强度、岩石材质指标mi等。

(2) 进行现场钻孔岩芯编录，获得不同地层的矿岩质量RMR，以此换算成地质强度指标GSI。

通过相关计算，获得的岩体力学参数如表1 所示。

表1 岩体力学参数Table 1 Rock mechanics parameters

结构面力学参数的确定，主要根据如下经验式进行估算:

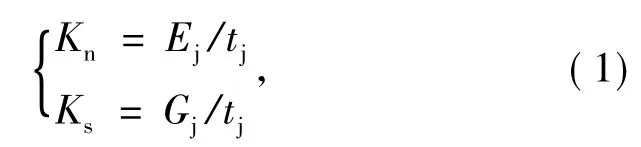
式中，Kn为结构面法向刚度; Ks为结构面切向刚度; tj为结构面厚度，一般tj=0.1 ～0.6 m; Ej为充填物质的变形模量;Gj为充填物质的剪切模量。综合参考其他类似工程及相关文献，选取的结构面力学参数如表2 所示。

表2 结构面力学参数Table 2 Structure mechanical parameters

1.2 数值计算模型的建立

所研究的矿山矿体属于典型的深埋急倾斜厚大矿体，倾角68° ～75°，矿体厚度为77.85 ～272.61 m，平均厚度为162.09 m，矿体最浅埋深－740 m，设计采用无底柱分段崩落法，自上而下分段进行回采。为掌握现场岩体节理分布情况，利用ZK －28 钻孔对－751 ～－1 006 m 区间进行了原位三维扫描( 如图1) ，其节理倾角以缓倾—中等倾角为主。

图1 钻孔摄像裂隙及产状分布Fig.1 Cracks and occurrence distribution from borehole camera

通过现场水压致裂法测试可知，钻孔横截面上大主应力值σ1随深度呈现良好的线性关系，如图2。

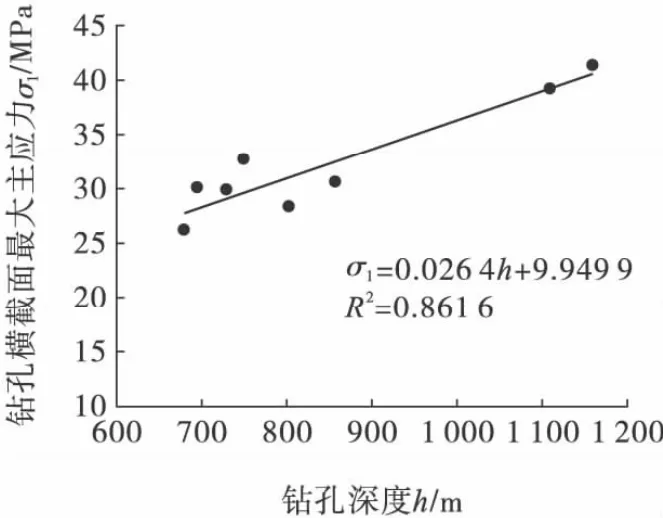
图2 钻孔横截面大主应力量值随钻孔深度回归曲线Fig.2 The regression curve of major principal stress magnitude with drilling depth on drilling cross-section

在地质调查的基础之上，将研究问题简化为平面应变模型，充分考虑节理、裂隙等地质因素，建立了典型剖面的二维计算模型，如图3 所示。模型尺寸宽为2 800 m，高为1 995 m，为消除边界条件对计算结果的影响，模型边界距开挖边界为3 倍的跨度。模型共计块体数4 563，节理面25 752 个，单元尺寸为100 m，共计29 013 万个单元，上部边界为自由面，其余各边界均为法向约束，块体和节理面都采用摩尔－库伦本构模型。

图3 计算模型Fig.3 Calculation model

2 不同条件下岩层移动特征分析

2.1 不同节理倾角对岩层移动的影响

为研究节理倾角对岩层移动的影响，分别建立了节理倾角为15°、30°、45°、60°和75°的计算模型，选取节理倾角为15°、30°的计算结果如图4 所示，图5为不同节理倾角下的地表沉降曲线。通过图4 和图5 可以看出:结构面对岩层的移动规律有着重要的控制作用。当优势节理倾角为15°时，矿石开采后，崩落以筒形陷落的形式塌落至地表，地表最大沉降量达到了30 m; 当节理倾角为30°时，沉降量和沉降范围有了明显的减小，最大沉降量约为10 m，崩落的发展趋势主要沿着优势结构面的方向发展，随着节理倾角的增大，对崩落的抑制作用越来越明显。由此可见水平节理对崩落有良好的促进作用;在其他条件一致的情况下，垂直或陡倾节理对岩体的崩落产生抑制作用，这种条件下矿体可能无法实现有效的崩落。

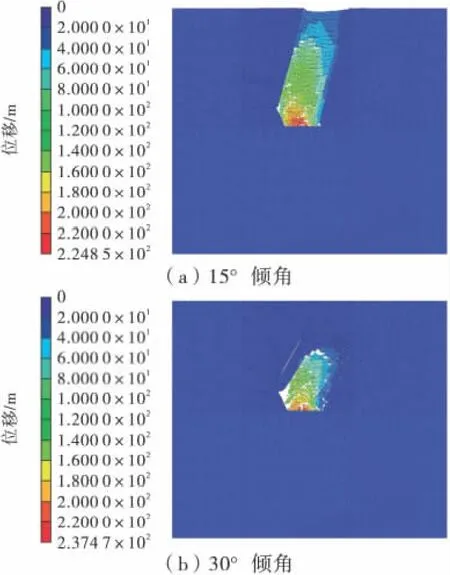
图4 不同节理倾角对岩层移动的影响Fig.4 Effects of different joint angle on strata movement

由此可见，结构面的存在对岩层移动规律有着重要的影响，结构面的分布决定了岩体的宏观变形、强度等特征。因此，现场通过节理裂隙的统计获得节理的统计参数是工程地质调查中一项非常重要的工作。

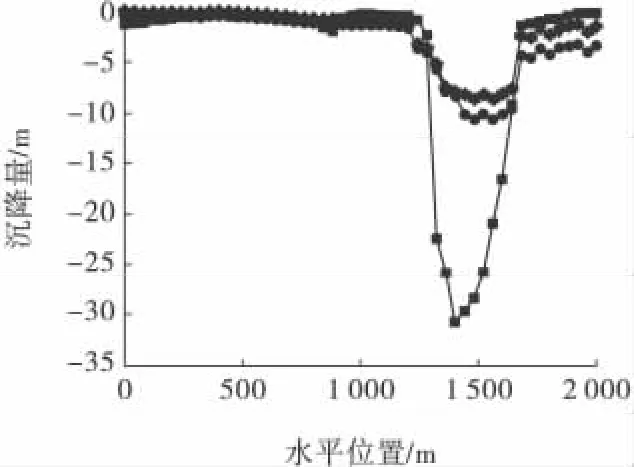
图5 不同节理倾角下的地表沉降曲线Fig.5 Surface settlement curve of different joint angle

2.2 不同侧压力系数对岩层移动的影响

对于深部开采的矿山，地应力通常以构造应力为主。在研究矿山地表塌陷变形与岩层移动时如果只考虑自重应力，如果忽视构造应力的影响，会使移动角、陷落角预测与实际情况出现较大偏差。由模拟结果( 如图6) 和沉降曲线( 如图7) 可以看出，对于深部开采的矿体，侧压力系数越大，崩落高度越小，这是由于随着侧向压力系数的增加，岩体在水平方向所受的夹制作用越来越强，抑制了围岩崩落的发展，表现出的宏观规律是地表沉降量和崩落高度逐渐变小。所以，对于构造应力比较大的矿山，地表相对不易出现塌陷。

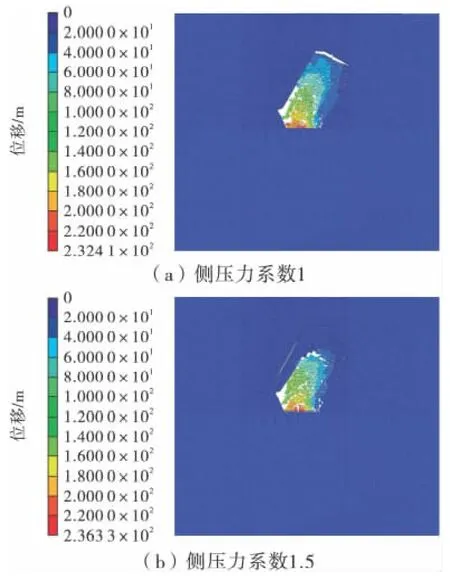
图6 不同侧压力系数对岩层移动的影响Fig.6 Effects of different lateral pressure coefficients on strata movement

2.3 不同开挖阶段对岩层移动的影响

图7 不同侧压力系数下地表沉降曲线Fig.7 Surface settlement curve of different lateral pressure coefficients

由模拟结果云图( 如图8) 可以看出，矿体从－752 m 水平开采到－812 m 水平时，地表几乎没有响应，采场顶部围岩发生了少量的冒落，当开采到－872 m 水平时，地表开始出现变形响应，开采到－932 m 水平时，地表出现了小范围的沉陷，此时采空区高度为120 m。开采到一期－1 052 m 水平时，承压拱的成拱机制破坏，地表出现了明显的崩落区、开裂区和变形区( 图8( d) ) 。这一结果也揭示了早期开采过程中，顶板存在形成承压拱的可能性，承压拱的存在可以承担覆岩及地表土的自重，对上覆岩层起到一定的支撑作用。承压拱形态会随着开挖的进行而不断演化，最终破坏承压拱的成拱机制，而导致采场上方覆岩断裂、地表塌陷。围岩变形和崩落与采空区形态密切相关，崩落法开采初期，顶板即可出现变形，当开采区达到一定体积后，承压拱失稳，顶板的变形就会演变成大范围的崩落。

3 结 论

(1) 优势结构面的发育特征对崩落发展过程有着显著影响，水平节理对崩落发展具有良好的促进作用，垂直或陡倾节理对岩体的崩落产生抑制作用，当优势节理呈倾斜状时，崩落沿优势结构面发展，但获得相对不大的崩落高度后即停止。

(2) 深部矿体开采过程中，构造应力对岩层移动的影响不容忽视，随着侧向压力系数的增加，岩体在水平方向所受的夹制作用越来越强，抑制了围岩崩落的发展，因此对于以构造应力场为主的矿山，围岩的可崩性相对较差。

(3) 不论是顶板崩落还是围岩变形，都与采空区形态密切相关，对于构造应力型深部开采矿山，开采初期承压拱的存在可以承担覆岩及地表土的自重，对上覆岩层起到一定的支撑作用。实际矿山生产中可通过开展开采顺序优化研究，在一定程度上实现对崩落发展过程的控制。

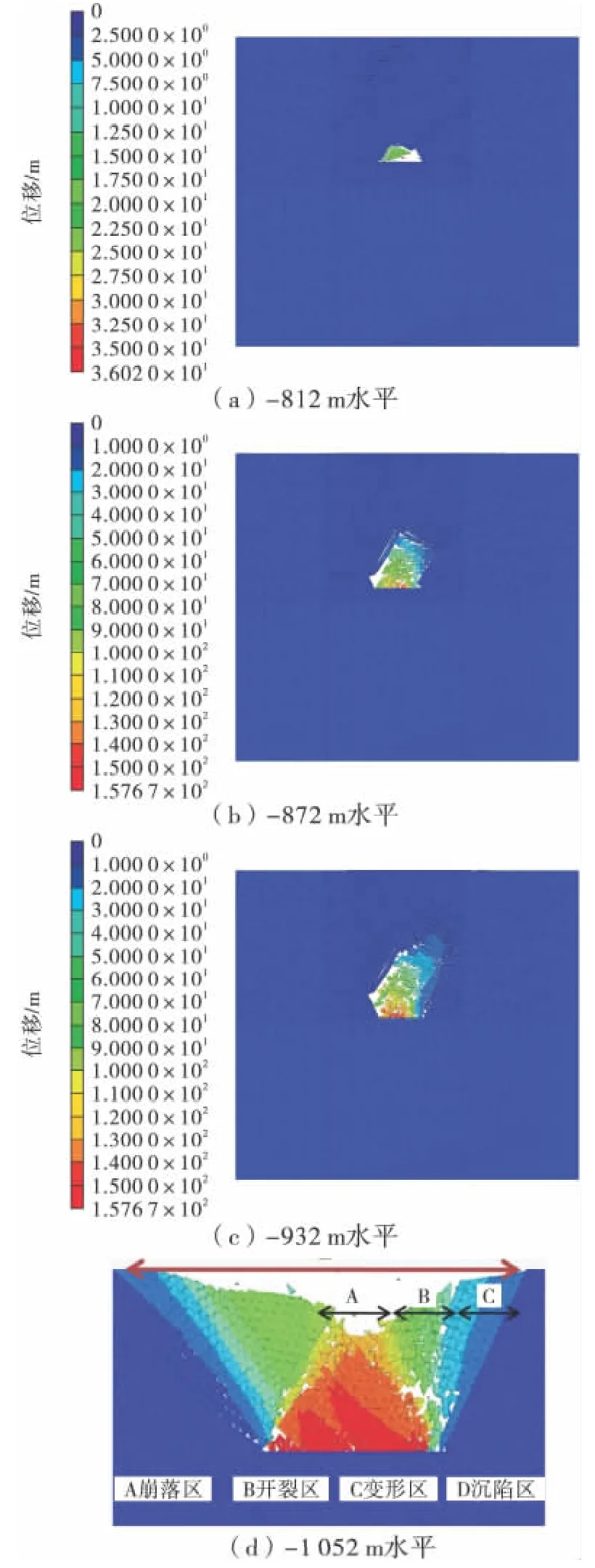
图8 不同开挖阶段对岩层移动的影响Fig.8 Effects of different excavation stages on strata movement

［1］ 胡建华，周科平，古德生，等. 基于连续采矿的顶板诱导崩落时变力学特性分析［J］. 采矿技术，2006，6(3) :157-160.

Hu Jianhua，Zhou Keping，Gu Desheng，et al. Mechanical properties analysis of roof caving induced by continuous mining［J］. Mining Technology，2006，6(3) :157-160.

［2］ 张国联，赵显涛. 岩体诱导冒落的数值模拟［J］. 东北大学学报:自然科学版，2012，33(8) :1190-1193.

Zhang Guolian，Zhao Xiantao. Numerical simulation on induced caving of rock mass［J］. Journal of Northeastern University: Natural Science，2012，33(8) :1190-1193.

［3］ 阿威尔辛C T. 煤矿地下开采的岩层移动［M］. 北京:煤炭工业出版社，1959.

Averroes C T.Rock Movement Underground Coal Mining［M］.Beijing:Coal Industry Press，1959.

［4］ 郭增长，谢和平，王金庄. 极不充分开采地表移动和变形预计的概率密度函数法［J］. 煤炭学报，2004，29(2) :155-158.

Guo Zengzhang，Xie Heping，Wang Jinzhuang. Applying probability distribution density function to predict the surface subsidence caused by subcritical extraction［J］. Journal of China Coal Society，2004，29(2) :155-158.

［5］ 郝兵元. 厚黄土薄基岩煤层开采岩移及土壤质量变异规律的研究［D］. 太原:太原理工大学，2009.

Hao Bingyuan. Study on the Law of Rock Movement and Soil Variation in Mining of Coal Seams of Thick Loess and Thin Bedrock［D］.Taiyuan:Taiyuan University of Technology，2009.

［6］ 胡 斌，刘永林，唐辉明，等. 武汉地铁虎泉—名都区间隧道开挖引起的地表沉降研究［J］. 岩石力学与工程学报，2012，31(5) :909-913.

Hu Bin，Liu Yonglin，Tang Huiming，et al. Research on ground subsidence due to tunnel excavation in Huquan-Mingdu section of Wuhan subway［J］. Chinese Journal of Rock Mechanics and Engineering，2012，31(5) :909-913.

［7］ 黄平路，陈从新. 露天与地下联合开采引起矿山岩层移动规律的数值模拟研究［J］. 岩石力学与工程学报，2007，26( S2) :4037-4043.

Huang Pinglu，Chen Congxin. Numerical simulation reseach on rock movement caused by surface mining and underground mining［J］.Chinese Journal of Rock Mechanics and Engineering，2007，26( S2) :4037-4043.

［8］ 王泳嘉. 离散元法及其在岩石力学中的应用［J］. 金属矿山，1986(8) :13-17.

Wang Yongjia. Discrete element method and its application in rock mechanics［J］. Metal Mine，1986(8) :13-17.

［9］ 张国权，盛建龙，孙明伟，等. 基于UDEC 的复杂条件下放顶引起的地表沉陷规律研究［J］. 金属矿山，2012(6) :145-148.

Zhang Guoquan，Sheng Jianlong，Sun Mingwei，et al. Study on the surface subsidence rule in roof caving under complex conditions cased on UDEC［J］. Metal Mine，2012(6) :145-148.

［10］ 李远耀，唐朝晖，陈仁全. 广西合山煤田浅埋煤层采空区塌陷机理数值分析［J］. 金属矿山，2014(3) :26-30.

Li Yuanyao，Tang Zhaohui，Chen Renquan. Numerical analysis on the mechanism of mining collapse in shallow seam of Heshan Coal Field，Guangxi［J］. Metal Mine，2014(3) :26-30.

［11］ Cundall P A. Formulation of a three-dimensional distinct element model-Part I，a scheme to detect and represent contacts in a system composed of many polyhedral blocks［J］. International Journal of Rock Mechanics and Mining Science ＆ Geo-mechanics Abstract，1988，25(3) :107-116.