基于耦合模型的尾矿坝稳定性对比分析

严 琼 吴顺川 李 龙 王强志

( 北京科技大学土木与环境工程学院，北京100083)

矿山资源的开采给社会带来丰富原材料的同时也给社会带来了一定的隐患和危害，尾矿库就是其一。近年来尾矿库溃坝事故时有发生，破坏性巨大，造成不可挽回的生命和财产损失。因此，尾矿库稳定性的研究愈发重要。现代科学技术的发展及计算机的应用已使人们在尾矿坝稳定性研究中有一些进展，然而，这些研究多采用有限元或有限差分的连续体模型算法［1］，而尾矿库宏观失稳破坏都是细观颗粒累积变形发展的结果，故已往的算法已不能满足分析的需要。

连续－离散耦合的算法及岩土体宏细观受力和变形相结合的分析自20 世纪80 年代初由Park 和Felippa 等［2］提出以来，已得到长足发展。目前，连续－离散耦合算法的开发，同时结合尾矿坝各影响因素的细观力学分析已成为工程界的热点研究课题。

1 连续－离散耦合计算方法原理及应用

1.1 连续－离散耦合原理概述

连续－离散耦合是岩土体数值模拟中计算方法的耦合，本离散、连续域分别采用颗粒单元法和有限差分法进行计算。颗粒单元( 以PFC 程序实现) 作为耦合离散域，被嵌入的有限差分单元( 以FLAC 程序实现) 在建模时需要预留与离散域一致的空间，离散域以单层颗粒围绕为边界。

图1 为耦合原理的简单图示，图1( a) 为预留离散域空间的连续域网格，箭头表示连续域节点受到来自离散域的作用力，图1( b) 为耦合离散域范围，周边深灰色颗粒为单层颗粒组成的耦合边界，黑色线段和黑点组成的沿深灰色颗粒走向的方框为节段序列，黑点所在的颗粒为控制颗粒，箭头表示颗粒的瞬时速度［5］。

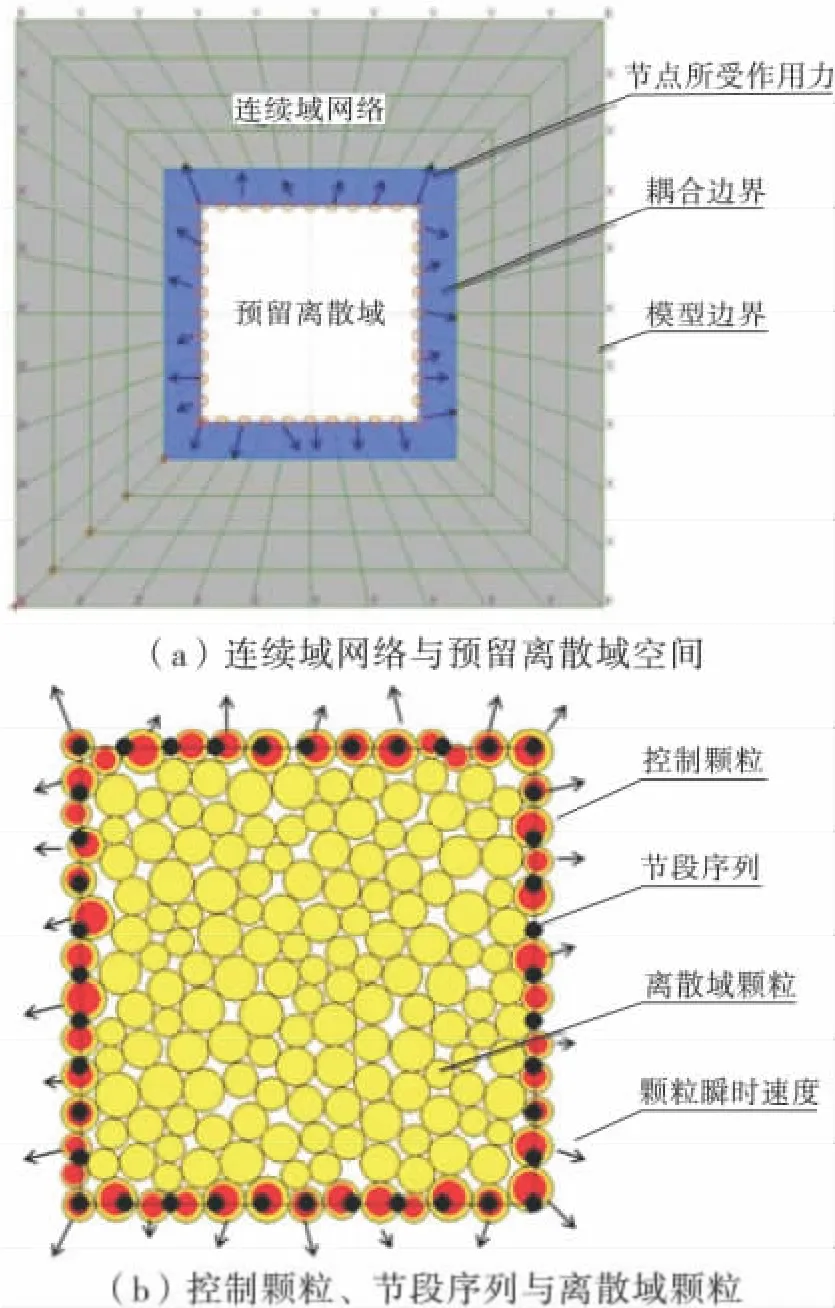
图1 耦合连续域与离散域示意Fig.1 Schematic diagram of coupling continuum and discrete domains

1.2 连续－离散耦合作用理论

节段端点坐标和长度分别为x0，x1和l，颗粒作用力为P，颗粒质心为xp。作用于节段端点的力为F0和F1:

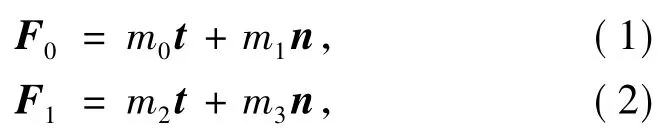
其中，t、n 分别为节点坐标系切向和法向的分量;m0，m1，m2和m3分别为与单位向量对应的变量。

节段端点坐标和长度分别由x0，x1和l 表示，颗粒坐标由xp表示，端点的速度由v0和v1表示。颗粒速度满足公式

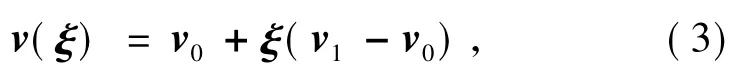
在此，ξ 是局部坐标，为

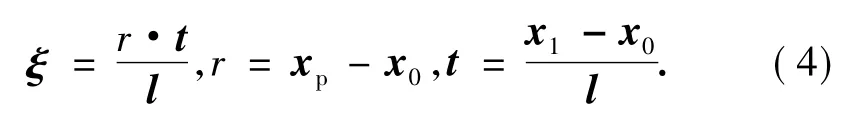
图2 为映射颗粒与节段节点反作用力与相应速率示意图。

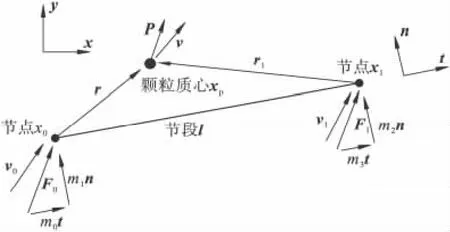
图2 映射颗粒与节段节点反作用力和相应速率示意Fig.2 Schematic diagram of the mapping particles，reaction force of segmented point and its associated velocity

1.3 耦合算法及细观力学分析在尾矿坝中的应用

张铎等［6］采用离散－连续耦合算法模拟了某尾矿坝边坡在尾矿充填前后潜在滑移带附近的宏细观力学特征，验证了尾矿坝在荷载增加中的渐进破坏的细观力学解释方法。张延军［6］采用了不同含水量对抗剪强度影响的模型，利用渗流耦合变形的弹塑性有限元法，证实由于渗流作用影响，边坡变形加大，最后形成潜在滑动面。周冬磊等［6］采用岩石力学伺服试验系统，对煤矿底板的岩样进行全应力－应变渗透试验，得到岩样裂隙在闭合、萌生、扩展过程中的渗透特性。缪海波等［6］应用渗流分析模块，模拟在初期坝不同透水情况、同长度条件下尾矿坝的渗流场变化规律，获得相应工况下的危险滑动面与危险系数。尹光志等［6］利用尾矿细微观力学与形变观测试验装置，对定量研究尾矿坝体细观结构特征和力学特性及探索水引起的尾矿坝灾变机制具有重要意义。

目前，离散－连续耦合的分析已经从方法上证实了其有效性，也在边坡稳定性研究中有了一定的尝试，但在考虑尾矿坝体水力作用引起的失稳破坏研究中，还未有深入的探索。本研究以应力－渗流耦合分析为基础，结合连续－离散耦合建模理论，对失稳破坏的尾矿坝建立数值分析耦合模型，对比动水作用和静水作用对尾矿坝的影响，对尾矿坝失稳的成因和机理从细观力学角度进行了合理解释。该方法弥补了现有尾矿坝长期采用连续元进行稳定性分析和连续－离散耦合计算中水力影响因素欠缺的不足，为边坡及尾矿坝稳定性分析方法进行了又一补充。

2 失稳尾矿坝工程案例简介

发生事故的山西襄汾尾矿库建于20 世纪80 年代，1992 年停止使用。尾矿库被封闭后，曾采取碎石填平、黄土覆盖坝顶、植树绿化下游坝坡、库区上方建设排洪明渠等闭库处理措施。新塔矿业公司通过拍卖购买了铁矿产权，本应重新修建新的尾矿库，但矿方却在旧库上挖库排放尾矿，造成尾矿库大面积液化，坝体失稳，并引发了这起特别重大的溃坝事故。

原废弃尾矿库建有二级坝，初期坝坝底高程约900 m，坝顶高程934 m，坝高约34 m，初期坝长约100 m，储矿量26.8 万m3;次级坝坝底高程934 m，坝顶高程950 m，坝高16 m，坝长约120 m，储矿量约10.3 万m3，尾矿库总库容约36.8 万m3。尾矿库溃坝后，尾矿库次级坝后缘120 m 范围内、深10 ～15 m的尾矿在平面上呈扇形依一定的坡度随水流一起冲出库区泄向下游，其泄出总量达19 万m3，将尾矿库下游的大量建筑物掩埋与破坏。

3 尾矿坝耦合模型构建与方案比选

3.1 应力－渗流耦合模型

浸润线作为尾矿坝的生命线，其高度与坝体稳定性休戚相关。从图3 尾矿坝失稳饱和状态剖面图可以看到，浸润线过高，干滩长度过短，坝体已具高势能饱和状态，是导致溃坝的直接原因。根据该尾矿坝溃坝资料，结合出水点水位高度，采用Flac 软件构建应力－渗流计算模型。根据该坝体运营模式，模型采取底层坝体先期平衡再进行上层堆载加压的方式。土体本构模型选取摩尔－库仑模型，边界条件包括应力和水力边界，应力场采用岩土体自重应力场，计算时步通过监测浸润线附近某点的孔隙水压力获得( 见图4，总时步约44 000 步) 。根据模型的几何剖面特征( 如图3) 和文献［10］的土层参数，模型计算参数见表1，应力－渗流模型和渗流、浸润线分布图如图5。

图3 襄汾尾矿坝失稳饱和状态几何剖面Fig.3 Geometric profile of instability ＆saturation state of Xiangfen tailings dam

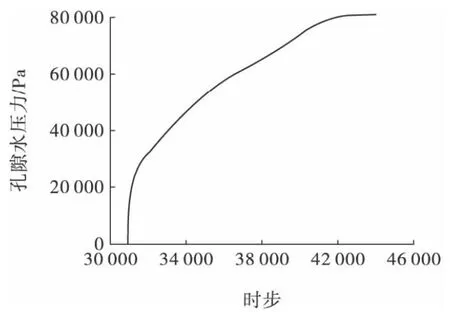
图4 节点孔隙水压力监测结果Fig.4 Monitoring result of the grid-point pore pressure

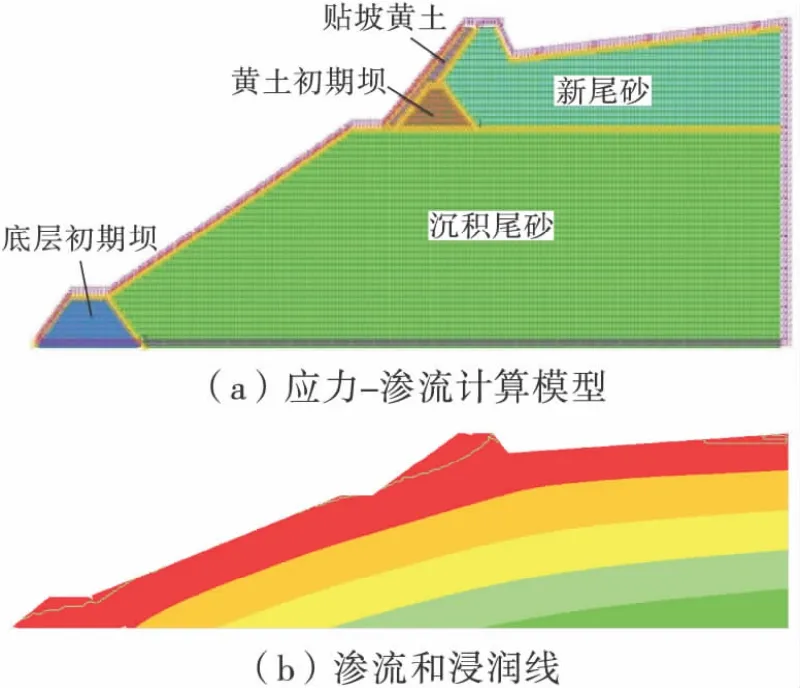
图5 襄汾尾矿坝应力－渗流计算结果Fig.5 The strees-seepage computed results of Xiangfen tailings dam

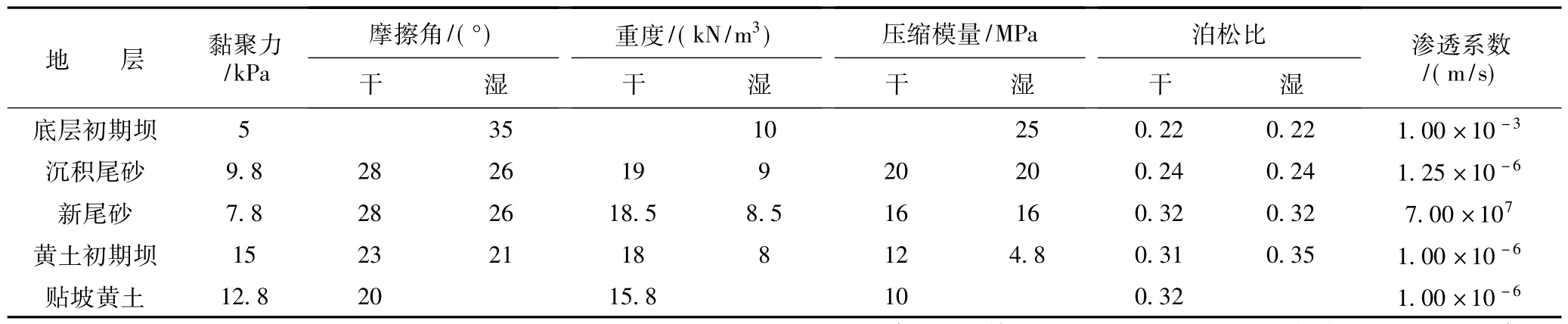
表1 计算模型参数Table 1 Parameters of the model

3.2 连续－离散耦合模型

3.2.1 细观参数选取

耦合模型的计算参数包括宏观参数和细观参数，宏观参数取值见表1 的沉积尾砂数据。而细观参数的选取是耦合计算中较为关键的步骤，不但要保证与连续域变形一致，也要确保能有效表征细观受力特征。根据宏观参数和材料特征，用实验室模型进行宏细观参数的反复调试，本研究分别采用离散元和有限差分模拟双轴压缩试验，当二者数值试验的结果接近时，可近似认为宏观与细观参数相互对应。离散元模型采用平行黏结模型，细观参数取值见表2，双轴试验的结果见图6。

表2 PFC 模型主要计算参数Table 2 Main calculation parameters of PFC model

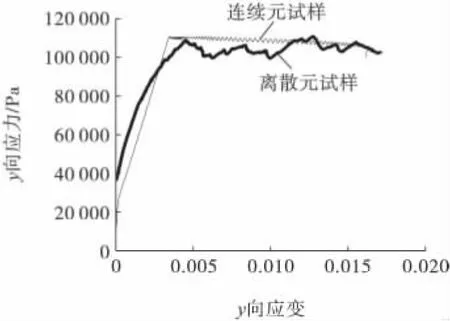
图6 双轴试验应力－应变曲线Fig.6 Stress-strain curve of biaxial tests

3.2.2 耦合方案比选

耦合模型的主旨是通过耦合域的离散模型，从细观力学的角度，分析宏观变形特征。不同的耦合方案，选取不同的耦合区域，耦合介质表现出的接触力和位移状况不同，但不会从整体上影响边坡的稳定性分析结果。

单就耦合域面积来说，越大越可能更多地显示颗粒体特征，但由于颗粒离散元试样从生成到耦合初始化，需要经过各种参数配比和调试，耦合域大小并不代表能获得合理的宏细观数据。此外，耦合区域所在位置的选取更是耦合方案的关键。对比图7 的各个耦合域方案，结合图8 坝体非耦合方式加载的位移变化，方案a 既能表现一级坝平衡后的特征，又能突出二级坝加载后的变形影响，可作为合理耦合域的选定范围。

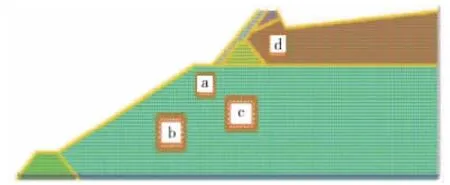
图7 尾矿坝耦合模型不同耦合域方案Fig.7 Respective discrete domain of tailings dam coupling model

3.2.3 耦合模型建立

连续－离散耦合模型的建立包含2 部分:连续域建模形式与应力－渗流模型的应力计算部分基本一致，采用FLAC 计算;离散域作为连续域中的一部分，采用PFC 计算，既通过边界颗粒与连续域进行数据交换，与连续域保持着受力和形变的一致性，也在该区域内显示出岩土体独有的细观力学特征。

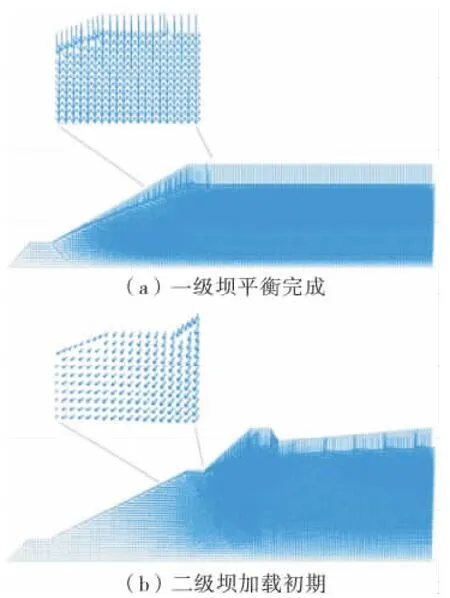
图8 尾矿坝模型加载过程及位移矢量Fig.8 Loading procedure and displacement distribution graph of tailings dam model

连续－离散耦合方法中连续域作为模型主体，在耦合初始化计算时，耦合域的离散元颗粒试样也需要赋以一定的应力状态，以契合和反馈连续域节点经虚拟做功传递的能量。离散元的初始应力场在试样生成后，采用双轴应力加载方式获得。

本案例作为含水的高势能饱和土体坝，水力因素必须考虑。但由于目前连续－耦合计算方法中，水力作用的研究尚不太成熟，因此，在应力－渗流计算结果的基础上，通过初步确定坝体浸润线，其上下分别采用不含水及含水饱和土体的计算参数，其中饱和土体应用有效应力原理，考虑静水浮力作用进行耦合计算。总体设定的计算时步为40 500 步，分设4 个监测时步对应坝体各计算状态( 见表3) ，计算参数参照表1 和表2，耦合计算模型见图9。

4 计算结果与分析

4.1 不同耦合模型的宏观变形对比分析

应力－渗流耦合方式作为较成熟的尾矿坝数值分析方法，可从应力和水力结合的方式，展示水力坡降的动态效果影响，但无法从细观力学角度解释岩土颗粒位移形变的成因，而连续－离散的耦合方法正弥补了这一缺陷。

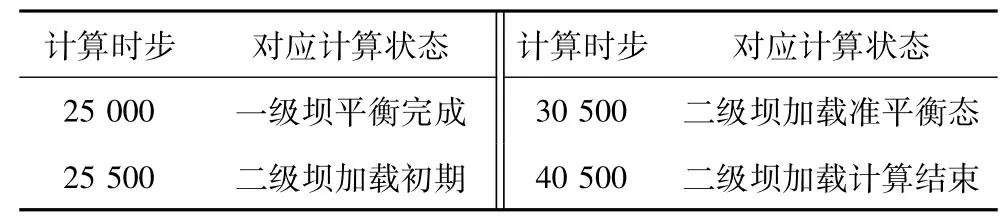
表3 尾矿坝计算状态和时步对照表Table 3 The computational state and time-step contrast of the tailings dam

图9 尾矿坝耦合计算中的模型Fig.9 The models in coupling calculation of the tailings dam

在本案例分析中，连续－离散耦合将动水作用简化为静水作用，从2 种耦合模型结果对比、位移发展和塑性变形效果方面，可对本案例的尾矿坝溃坝成因给予详尽的分析。由图10、图11，2 种分析方法位移矢量及塑性变形图表明:应力－渗流耦合模型计算平衡的塑性变形区域与连续－离散耦合模型基本一致，坝体在2 种计算模型下的宏观变形结果基本相同，且与该尾矿坝溃坝实例一致( 如图12) 。

4.2 连续－离散耦合模型的失稳表征协同分析

本研究中连续－离散耦合的数值计算方法采用有限差分FLAC 和离散元PFC 协同计算，可获得对已失稳襄汾尾矿坝分析对象较为契合的结果。连续－离散耦合模型在饱和土体中根据有效应力原理，采用浮重度的计算参数，计算结果的位移已达失稳态势。通过对比2 个模型的位移和塑性变形图( 图10、图11) ，可以看出: 基于连续－耦合模型的静水作用计算方法，可以有效表征含水尾矿坝体失稳的情况，虽位移矢量大小与应力－渗流模型有差别，但坝体失稳的发展趋势较为一致，用于本例的宏细观分析，可达到较好的分析效果。

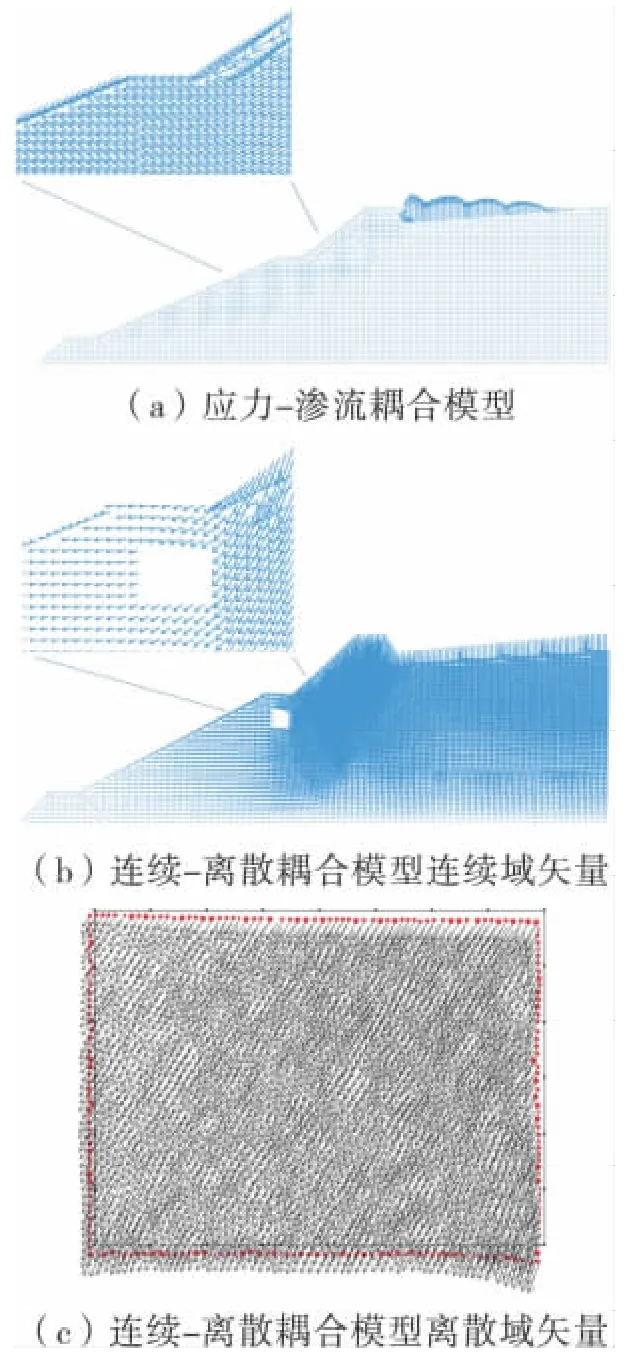
图10 尾矿坝位移矢量Fig.10 The displacement vector diagram of the tailings dam

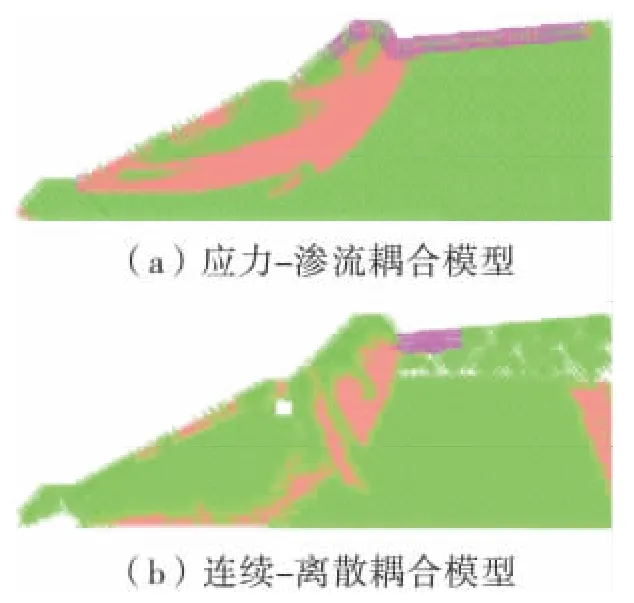
图11 尾矿坝塑性变形Fig.11 The plastic deformation diagram of the tailings dam

5 结 论

(1) 应力－渗流耦合方法作为成熟的尾矿坝稳定性研究方法，相比连续－离散耦合方法，在宏观上能较合理地表征边坡失稳态势，也能为后者提供浸润线和渗流方向等研究基础数据。结果表明，二者在坝体位移的失稳发展和坝体塑性变形方面呈现较为一致的趋势。

图12 襄汾尾矿坝溃坝实例Fig.12 The break case of XiangFen tailings dam

(2) 根据有效应力原理和应力－渗流耦合的浸润线计算结果，对坝体进行土层饱和与非饱和参数的划分，引入浮重度参数，可对尾矿坝进行连续－离散耦合的计算分析，但所需的平衡时步比应力－渗流耦合的计算时步少，位移矢量大小也明显偏小，但其位移矢量值已达失稳状态。

总之，计算结果分析表明，采用的基于耦合模型的尾矿坝稳定性分析，可有效揭示山西襄汾尾矿坝溃坝的宏细观变形规律，具有一定的科学应用价值。

［1］ 马萃林，朱 明，王建华. 有限差分法FLAC 在边坡稳定性分析中的应用［J］.中国矿山工程，2008，37(5) :19-22.

Ma Cuilin，Zhu Ming，Wang Jianhua.Application of finite difference method FLAC in analyzing slope stability［J］.China Mine Engineering，2008，37(5) :19-22.

［2］ Park K C，Felippa C A.Partitioned analysis of coupled systems［C］∥Belytschko T，Hughes T J R，et al. Computational Methods for Transient Analysis.Amsterdam:［s.n.］，1983:157-219.

［3］ Felippa C A，Park K C. Staggered transient analysis procedures for coupled-field mechanical systems: formulation［J］. Computer Methods in Applied Mechanics and Engineering，1980，24(1) :61-111.

［4］ Onate E，Rojek J.Combination of discrete element and finite element methods for dynamic analysis of geomechanics problems［J］. Computer Methods in Applied Mechanics and Engineering，2004，193:3087-3128.

［5］ Itasca Consulting Group Inc..PFC2D version 4.0 Verification Problems and Example Applications［M］. Minnesota: Itasca Consulting Group Inc.，2008.

［6］ 张 铎，刘 洋，吴顺川，等. 基于离散-连续耦合的尾矿坝边坡破坏机理分析［J］.岩土工程学报，2014，36(8) :1473-1482.

Zhang Duo，Liu Yang，Wu Shunchuan，et al. Failure mechanism analysis of tailing dams based on coupled discrete and continuous method［J］. Chinese Journal of Geotechnical Engineering，2014，36(8) :1473-1482.

［7］ 张延军.边坡渗流耦合变形分析方法的研究及其应用［J］.吉林大学学报:地球科学版，2006，36(1) :103-107.

Zhang Yanjun.The study of the analysis method of seepage coupled deformation in slope and its application［J］.Journal of Jilin University:Earth Science Edition，2006，36(1) :103-107.

［8］ 周冬磊，王连国，黄继辉，等. 裂隙岩体应力渗流耦合规律及对底板隔水性能研究［J］.金属矿山，2011(11) :53-57.

Zhou Donglei，Wang Lianguo，Huang Jihui，et al.Coupled behavior of stress and permeability in fractured rock masses and its study of water isolation［J］.Metal Mine，2011(11) :53-57.

［9］ 缪海波，殷坤龙，郭付三，等. 金属矿山尾矿坝渗流场模拟及稳定性数值分析［J］.金属矿山，2010(3) :134-138.

Miao Haibo，Yin Kunlong，Guo Fusan，et al.Seepage field simulation and numerical analysis of stability of metal mine tailings Dam［J］.Metal Mine，2010(3) :134-138.

［10］ 尹光志，张千贵，魏作安，等.尾矿细微观力学与形变观测试验装置的研制与应用［J］. 岩石力学与工程学报，2011，30( 5) :926-934.

Yin Guangzhi，Zhang Qiangui，Wei Zuoan，et al. Development and application of observation testing apparatus for micromechanics and deformation of tailings［J］.Chinese Journal of Rock Mechanics and Engineering，2011，30(5) :926-934.

［11］ 董成会.尾矿堆积坝溃坝分析及数值模拟研究［D］.南昌:南昌大学，2012.

Dong Chenghui. Analysis of Dam-break and Numerical Simulation Study on Tailings Stacking Dam［D］.Nanchang:Nanchang University，2012.