低地板铰接列车动态包络线计算

罗 仁 李 然 彭祎恺

(西南交通大学牵引动力国家重点实验室 成都 610031)

低地板铰接列车动态包络线计算

罗 仁 李 然 彭祎恺

(西南交通大学牵引动力国家重点实验室 成都 610031)

通过分析70%和100%低地板铰接列车通过直线轨道和曲线轨道时的位置和运行姿态，推导铰接列车几何曲线通过算法。采用CJJ96-2003车辆动态包络线计算方法，根据铰接列车的结构特点对计算公式进行修正。结合列车姿态，提出铰接列车的动态包络线计算公式和计算方法。编写了计算机仿真软件，实现低地板铰接列车的几何曲线通过和动态包络线自动计算。

低地板铰接列车；动态包络线；几何曲线通过；限界

1 研究现状及计算流程

随着我国城市建设的快速发展，多个城市已开通或正在建设轻轨交通，一般采用70%或100%低地板轻轨列车。另外还有出口国外的低地板列车项目。我国现在只有大铁路和地铁车辆限界标准，没有低地板轻轨列车限界标准。而低地板轻轨列车车厢间采用铰接结构，与大铁路和地铁车辆结构完全不同，不能照搬其限界标准和计算方法。

1.1 研究现状

1.2 计算流程

根据轻轨列车的铰接关系，以及车体和转向架间的约束关系，可以得到列车各车体之间的极限姿态关系。例如，3辆车铰接的70%低地板列车，其车辆间的姿态为Z字形，中间转向架和车体间由牵引拉杆构成摇头约束，从而约束列车的摇头姿态；而前后车体间的铰接，约束了车体的点头和侧滚。通过对列车在直线轨道和曲线轨道上的姿态分析，可以得到列车在线路上各位置时的姿态。通过对几何曲线通过分析，并结合车辆的动态偏移，就可以得到列车的动态包络线。

我国地铁车辆采用动态包络线计算标准CJJ96—2003 《地铁限界规范》，该方法使用简便，考虑的因素比较全面，其原理可以适用于各种四轴轨道车辆。通过对该方法的适当修改，使其适用于两轴车辆，进而结合轻轨列车姿态，就可以得到轻轨列车的动态包络线计算方法。当采用动力学方法计算动态包络线时，轻轨列车动力学建模比较复杂，需要的参数很多且很难通过计算得到车辆间的极端姿态；本文的计算方法需要的参数相对较少，且可以考虑列车的极端姿态。整个计算流程如图1所示。

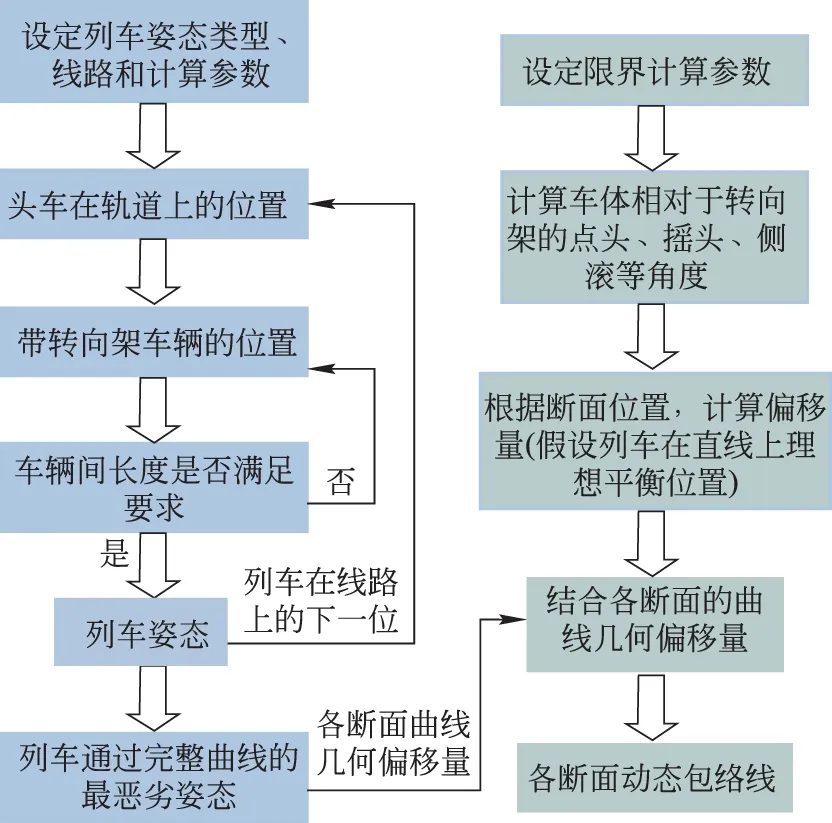
图1 计算流程

针对不同的曲线线路，列车在通过曲线的过程中姿态不断发生变化，最危险的位置与车辆所处的纵向位置有关。为了更加准确地模拟列车姿态，事先建立线路模型，生成线路中心线的离散点坐标。线路包括直线、缓和曲线及圆曲线的各种组合，也可以是任意曲线。在以下各节中，CG代表车辆限界(car gauge)，SG代表建筑限界(structure gauge)，VP代表车辆轮廓(vehicle profile)。

2 几何曲线通过计算方法

铰接列车几何曲线通过计算方法如图1左边所示。传统的作图法不能准确地综合考虑到车辆姿态和车辆长度，作图结果存在误差，尤其是通过复杂的小半径曲线工况，例如带夹直线的S型曲线，或者有缓和曲线的直线。本文首先设置带转向架车辆的姿态，通过纵向位置的迭代，可以保证准确的车体和车钩长度，从而保证计算精度。考虑转向架相对于轨道中心线存在横移时，迭代方法同样能准确计算。

2.1 3辆车铰接的70%低地板列车

列车通过曲线时的姿态如图2所示，中间车体的摇头受转向架相对于轨道的姿态、车体与转向架间的牵引拉杆限制；而中间车的姿态限制了前后车辆的姿态，从而整个列车在曲线上的姿态就可以确定。图2是考虑转向架相对于轨道存在横移的通用工况，需要通过迭代才能准确获得列车姿态。当转向架在轨道中心线上时就不需要迭代。直线轨道上的计算原理相同。

图2 3辆车铰接列车姿态

2.2 5辆车铰接的100%低地板列车

5辆车铰接的100%低地板列车如图3所示。每辆车之间均可以相对摇头，但转向架与车体的相对摇头受到限制；列车各车体的相对点头只在部分铰接位置得到释放，从而保证列车处于稳定状态。从左到右的车辆分别定义为1车到5车。

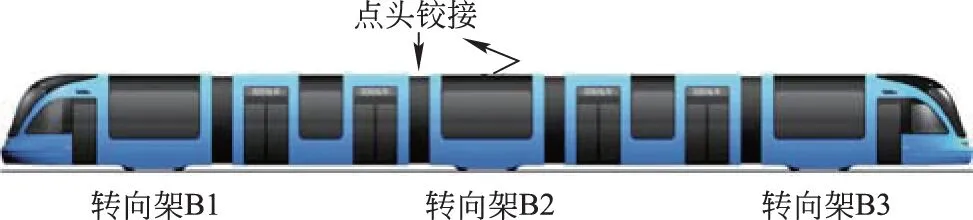
图3 5辆车铰接列车

对于100%低地板轻轨列车，车辆间容易形成Z字型姿态。为了得到更加通用的算法，考虑5辆列车连挂的工况，即计算车辆姿态时考虑到第2列第1车救援连挂工况。根据带有转向架车辆的摇头方向，有多种列车姿态，4种最恶劣的列车姿态如下：

1) 1车逆时针，3车顺时针，5车逆时针，第2列1车顺时针；

2) 1车顺时针，3车逆时针，5车顺时针，第2列1车逆时针；

3) 1车逆时针，3车逆时针，5车逆时针，第2列1车逆时针；

4) 1车顺时针，3车顺时针，5车顺时针，第2列1车顺时针；

其中前两种工况，中间车偏向线路的一侧。后两种工况，中间车Z字型反向，两端分别处于线路的两侧。图4是列车姿态示意图，为了便于观看，将垂向的绘图比例放大；在姿态3和姿态4中车钩长度比较长，是由于绘图比例造成的。需要注意的是，这里带转向架车体的摇头角度，可以包含了轮轨间隙、一二系横向位移的作用，也可以仅考虑理想姿态。

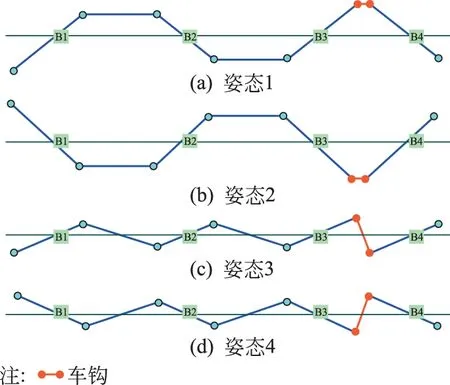
图4 列车的相对姿态

图4中各圆点表示车间铰接结构，各粗线表示车辆中心线，细线表示线路中心线。B表示转向架，左边2条没有转向架的粗线表示悬浮车体，右边没有转向架的粗线表示2列车连接的车钩。

3 动态包络线计算

动态包络线的计算流程如图1所示，需要首先完成几何曲线通过计算，确定车体计算断面在整个曲线通过中横向偏移量的最大值。然后根据修订的动态偏移量计算公式，计算得到车辆断面的偏移量。将两者叠加，得到列车通过曲线时的动态包络线。通过该方法，也可以得到列车通过曲线时动态包络线的连续变化过程。

3.1 动态偏移量计算公式

针对2轴车辆，先不考虑车体相对于转向架的摇头，修改CJJ96—2003[9]的动态包络线计算公式。以下各公式中未说明的参数，与CJJ96—2003标准中参数的意义相同。CJJ96—2003考虑了横风力、横向加速度、载荷不对称对车体侧滚的贡献，且将前两项考虑为随机量。这样的优点是可以更加准确地考虑外载荷对侧滚的影响，缺点是不能准确考虑垂向止挡的作用，在大风作用下计算结果偏大[6]。笔者采用另一种方法，将公式中的以上3项去掉，直接设置车体侧滚角。侧滚角可以事先通过静力平衡计算得到，并且可以考虑止挡的作用。

3.1.1 车体横向偏移(横移和侧滚同向)

(1)

1) 横向位移放大系数考虑轴距而不是定距；

2) 轮轨间隙、一系动态横向位移、二系摇头止挡引起的摇头角已经包含到列车姿态中；

3) 车体侧滚由侧滚角β乘以控制点到车体侧滚中心Yc的高差得到，侧风、横向加速度、载荷不对称等因素不在公式中体现。

3.1.2 车体竖向向下偏移由于前后车辆铰接，对前后车体垂向位移有限制，所以一系和二系垂向变形均只能改变车体整体的浮沉量，而不能改变点头情况。这里引入每辆车的点头角度和侧滚角度。

(2)

1) 为了考虑各种止挡和铰接的作用，引入车体的侧滚、点头角度；原公式中的侧风力、横向加速度、载荷不对称等因素不在公式中体现；

2) 车体点头角α、车体侧滚角β 引起的偏移量，直接由小角度假设计算得到。

3.1.3 车体竖向向上偏移和车体竖向向下偏移公式一样做相同的改动。

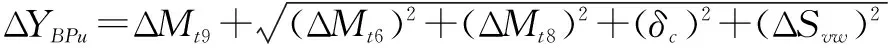
(3)

3.1.4 其余部件计算公式转向架构架、簧下、车轮、受流器等计算公式和CJJ96—2003完全相同。受电弓横向偏移公式和以上车体公式相同，只是需要在根号中加入“(ΔShd)2”项；垂向公式和以上公式相同。

考虑到横移和侧滚同向时的车体横向偏移量比较大，而车体超限一般都发生在横向，所以本文仅考虑这种工况。如果要考虑横移和侧滚反向，将CJJ96—2003的公式进行类似的更改即可。

3.2 车体的摇头、侧滚由于车辆下方仅有一台转向架，为了有效地约束车体的摇头姿态，在转向架前后的端部和车体上设置横向止挡，间隙为Δw3。当转向架前后一系弹簧的横向变形反向时，也会引起转向架构架和车体的摇头。另一个限制摇头运动的因素是轮轨间隙，这和一系横向位移引起的摇头类似。以上3种因素引起的车体相对于线路的摇头角为：

(4)

其中，Lstop表示二系横向止挡距离转向架中心的纵向距离。当通过其他方式约束车体和构架摇头时，公式(4)中第3项直接设为该约束角度。

一系和二系悬挂垂向变形引起的车体相对于线路的侧滚角如公式(5)所示。根据实际情况，Δfp和Δfs可以是一二系悬挂的正常动挠度，也可以是一二系悬挂的垂向止挡间隙。

(5)

根据列车的受力状态(包括侧风力、横向加速度)和各弹簧的悬挂刚度，通过静力平衡，可以确定一系和二系弹簧的垂向变形量。

3.3 车体的点头

由于铰接约束，车体间的点头示意见图5。根据各转向架的一系和二系垂向变形量，以及车轮磨耗、钢轨磨耗、轨道垂向不平顺，计算车体在转向架位置的垂向位移，进而计算得到列车各车体的点头角度α。

4 算例

本节以某3辆车铰接的70%低地板和某5辆车铰接的100%低地板列车为例，分析几何曲线通过时的列车姿态，并计算动态包络线。100%低地板列车悬浮车前后铰接点纵向间距6 900 mm，中间拖车前后铰接点纵向间距4 800 mm，头车转向架中心距铰接点纵向2 500 mm，头车车钩长度1 120 mm，头车车钩距转向架中心纵向距离5 200 mm。100%低地板列车考察11个断面，以S1到S11表示，如图6所示。

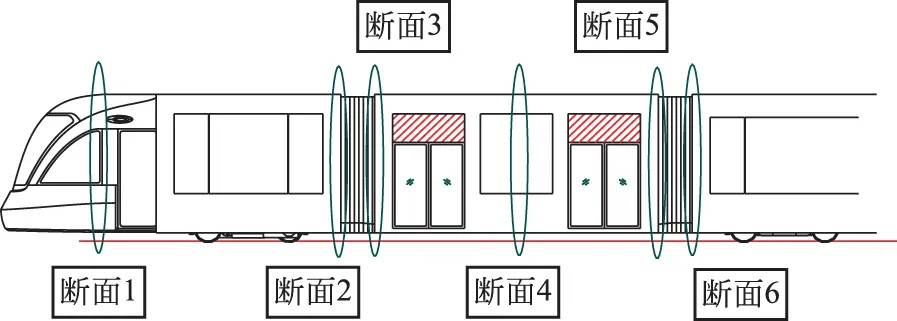
图6 计算轮廓断面位置

前动车头部最内端的最大轮廓，距离相邻转向架中心2 050 mm；前动车头部最外端的最大轮廓，距离相邻转向架中心3 150 mm；前悬浮车车体前端，距离车体中心3 150 mm；前悬浮车车体纵向中心；前悬浮车车体后端，距离车体中心3 150 mm；中间拖车最外端的最大轮廓，距离相邻转向架中心2 050 mm；后面5个断面分别在后悬浮车体、后动车上的相应位置，与前5个断面对称。

4.1 100%低地板列车几何曲线通过

由于列车处于曲线上不同位置会影响车间姿态和横向偏移量，车轮之间的夹角、车钩摆臂角也会受到影响。为此，对于一个完整的曲线，需要计算列车处于不同位置时的各种数据。

以列车通过一个半径25 m的完整曲线为例，计算得到各铰在水平面的夹角，如图7所示。图8是计算的11个断面典型列车姿态下的横向偏移量。

图7 列车在曲线的位置对车体间夹角的影响

图8 列车姿态1时的计算断面偏移量

从计算结果可见：

1) 列车在曲线中的位置对偏移量有较大的影响；

2) 计算断面一般在圆曲线或者直线上的偏移量较大，某些情况下在缓和曲线的偏移量更大；

3) 列车的不同姿态对偏移量影响较大；

4) 姿态1的曲线内侧和外侧偏移量均最大。

根据以上结果，考虑列车通过整个曲线(包括直线+缓和曲线+圆曲线+缓和曲线+直线)，分别计算得到每个断面向曲线内侧的最大偏移量、向曲线外侧的最大偏移量，然后用于计算动态包络线。

4.2 100%低地板列车动态包络线

针对某5辆车铰接的100%低地板轻轨列车在直线轨道和各种半径曲线轨道上运行的工况，计算得到列车在空车状态下11个关键断面的动态包络线。计算车辆半宽1 325 mm。

根据前面的几何曲线通过分析，姿态1时的曲线偏移量最大，所以动态包络线也最大，故在各种曲线半径下，只计算姿态1的动态包络线。半径20 m曲线轨道上车辆动态包络线的计算结果如图9所示。

图9 通过半径20 m曲线轨道的动态包络线

从计算结果可见，车体动态包络线横向偏移量与断面距离转向架的纵向位置有关。断面1和断面3在直线轨道上的横向偏移量最大，断裂8和断面11在曲线轨道上的横向偏移量最大。受电弓位于中间转向架上方，所以在直线和曲线轨道上动态偏移量接近。曲线轨道与直线轨道相比，其动态包络线最大值增加量：曲线内侧为174.9 mm，曲线外侧为307.3 mm。

为了分析曲线半径对动态包络线的影响，计算了列车完整地通过不同半径曲线时的动态包络线横坐标最大值，如表1所示。从计算结果可见，曲线外侧的包络线横坐标最大值随着曲线半径的增大而减小，最后趋于直线轨道的值。曲线内侧包络线横坐标最大值，在曲线半径小于200 m时，随着曲线半径的增大而减小，之后保持与直线轨道相同的值。主要原因是本计算是基于一个完整的曲线通过开展的，包含了直线部分。在圆曲线部分，曲线内侧偏移量在曲线半径大于200 m时，可小于直线轨道时的偏移量，但这个缩小量小于10 mm，具体结果不再列出。由于大半径曲线内侧的缩小值很小，且出于完整曲线的安全性考虑，建议大半径曲线内侧的车辆限界按照直线轨道设置。

表1 100%低地板列车动态包络线横坐标最大值

4.3 70%低地板列车连挂通过曲线

70%低地板列车的铰接和转向架布置与100%低地板列车不同，计算公式需要作相应的修正，但计算方法相同。图10是某70%低地板列车2列车连挂救援工况下，救援车钩与前后车体的夹角计算结果，列车尺寸如图所示。S型曲线半径25 m，夹直线长度2 m。

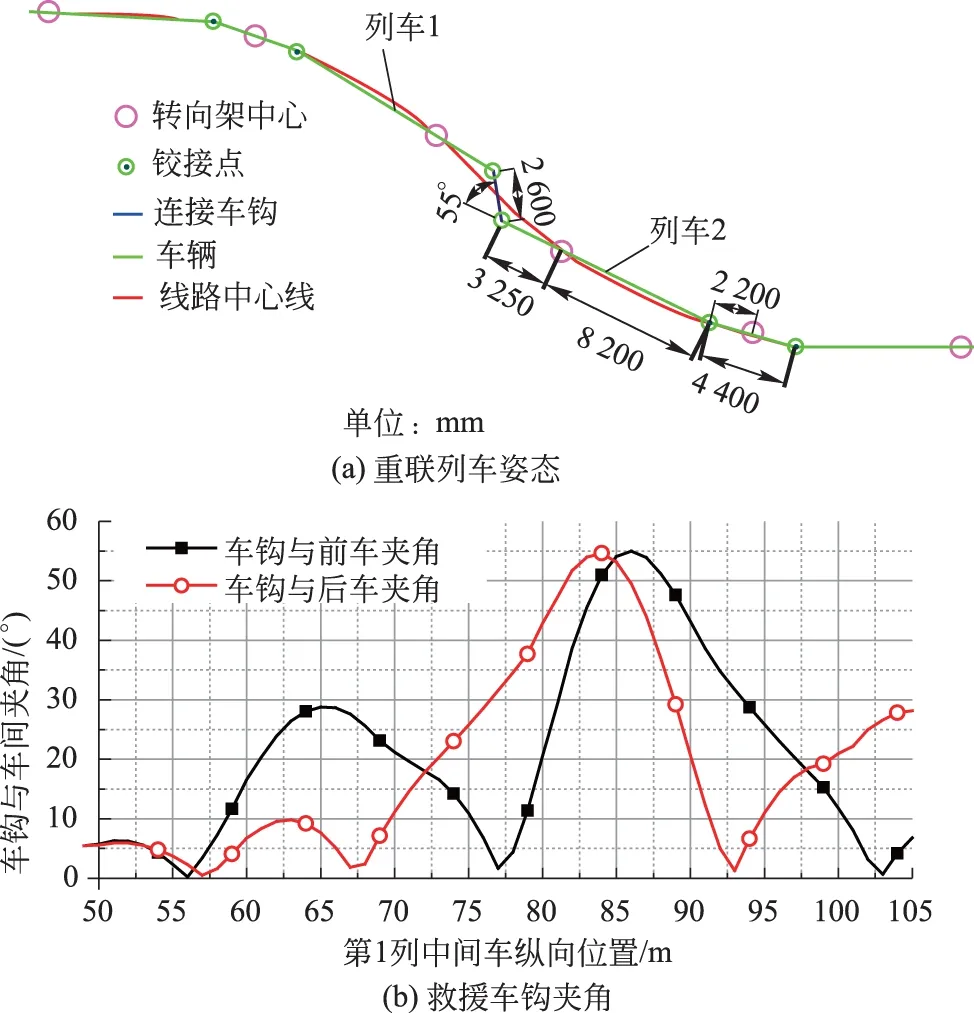
图10 70%低地板列车救援工况

从计算结果可见，救援车钩与车体夹角最大达到55°。在计算过程中，通过设置不同的车间姿态和转向架横移方向，可以模拟前列车牵引、后列车推动等各种工况。救援车钩最大夹角：前列车牵引时为46°,理想位置时为49°,后列车推动时为55°。可见救援工况采用前列车牵引有利于通过小半径曲线。

通过对列车完整曲线通过的计算分析，得到70%低地板列车在不同半径曲线线路上的曲线几何加宽量如表2所示。

表2 70%低地板列车曲线几何加宽量

5 结语

根据70%低地板铰接列车和100%低地板铰接列车的结构特点，采用列车姿态计算与动态包络线计算相结合的方法，计算车辆动态包络线。对CJJ96—2003的动态包络线公式进行了修改，以适应铰接列车；同时为了考虑悬挂止挡，非线性公式中直接带入车体侧滚角、点头角。车体的摇头角在列车几何曲线通过计算中已经考虑。最后给出了几何曲线通过和动态包络线的算例。采用本方法可以模拟低地板铰接列车通过各种几何曲线，并计算通过完整曲线时的动态包络线变化过程。与动力学方法相比，本方法简单快捷，考虑因素更加全面，且可以考虑极端姿态。

[9] CJJ 96—2003地铁限界标准[S].北京:中国建筑出版社, 2003.

(编辑：曹雪明)

Dynamic Envelope Curve Calculation of Low-floor Articulated Trains

Luo Ren Li Ran Peng Yikai

(Traction Power State Key Laboratory, Southwest Jiaotong University, Chengdu 610031)

By analyzing the position and posture of 70% and 100% low-floor articulated trains negotiating straight and curved tracks, the algorithm of geometric curve-passing for articulated trains are derived. Using the vehicle dynamic envelope curve calculation method in CJJ96-2003, the formula was corrected based on the structural characteristics of articulated trains. Then the calculation formula and method of dynamic envelope curve were introduced in line with the train's posture. The geometric curve-passing and dynamic envelope curve of low-floor articulated trains are automatically calculated by programming computer simulation software.

low-floor articulated trains; dynamic envelope; negotiation of geometric curve; gauge

罗仁，男，工学博士，副研究员，从事车辆系统动力学研究，luoren@swjtu.cn

U231.12

A