基于广义动态模糊神经网络的短时车站进站客流量预测

李春晓 李海鹰 蒋 熙 许心越 赵阿群

(1.北京交通大学轨道交通控制与安全国家重点实验室 北京 100044；2.北京交通大学交通运输学院 北京 100044；3.北京交通大学计算机与信息技术学院 北京 100044)

基于广义动态模糊神经网络的短时车站进站客流量预测

李春晓1,2李海鹰1蒋 熙1许心越1赵阿群3

(1.北京交通大学轨道交通控制与安全国家重点实验室 北京 100044；2.北京交通大学交通运输学院 北京 100044；3.北京交通大学计算机与信息技术学院 北京 100044)

轨道交通；广义动态模糊神经网络；短时客流预测；进站量

1 研究背景

随着城市轨道交通进入网络化运营模式，线网规模和复杂性不断增加，对城市轨道交通运营管理提出了更高的要求，短时客流预测不仅是运营管理与资源配置的基础[1]，还能为运能分析及运量匹配提供有效的数据支持。因此，实时准确的短时客流预测是实现轨道交通系统高效、有序运行的重要保障。

相比中长期客流，短时客流具有更强的随机性、高度非线性等特点，使得传统的预测方法如时间序列、非参数回归模型等不适用于短时客流预测。短时客流预测通常集中在BP神经网络、支持向量机等方法的研究上，但它们存在以下问题：BP神经网络对初始权值非常敏感，算法稳定性差，收敛速度水平较低，网络的泛化能力差[2]；支持向量机则难以训练大规模的样本数据，存在多分类问题求解困难的弊端，而轨道交通的客流数据量庞大，会耗费大量机器内存与运算时间，故这类方法有很大的局限性[3]。

2 轨道交通车站进站客流特性

城市轨道交通车站小时进站客流随城市生活的节奏变化在一天内呈动态起伏状分布，车站小时客流一般有5种分布类型[8]：单峰型、双峰型、全峰型、突峰型和无峰型。由于轨道交通系统日常服务的通勤出行比例较高，工作日时遵从早出晚归的规律，所以通常客流在一天内呈双峰型分布。

工作日与休息日的进站客流分布有明显区别：周一至周五的进站量明显高于休息日，并有明显的早晚高峰现象，呈现很强的规律性，而休息日的进站客流相对分散，分布比较均衡，如图1所示。

图1 北京地铁2号线A站一周内各日的分时进站量

节假日也影响车站短时进站客流分布，十一节假日期间的进站量明显小于前后两周的进站量。节假日期间部分市民选择出去旅游，通勤客流也大大减少，如图2所示。

图2 北京地铁13号线B站十一假期及前后两周进站量

同时，突发事件如举办大型活动、地铁信号设备故障及天气的骤然变化等也会对短时客流分布产生较大影响。如2013年12月北京地铁13号线信号设备发生故障，当日13号线全线客流较平日减少7.37%，约6.29万人次；2013年9月北京地铁4号线ATS(自动列车监控系统)工作站故障，当日4号线客流较平日减少15.97%，约20万人次。

因此，在时间方面，客流受到节假日、工作日、双休日及时段影响；从突发事件的角度，客流受到重大活动、骤然天气变化等不确定因素的影响。不确定因素会引起进站客流的随机波动，但总体上具有周期变化(如双峰型)的规律。进站客流曲线具有相似性的特点使得客流预测模型可以发现样本数据规律，实现进站量预测。

3 基于GDFNN的客流预测模型

3.1 选择模型输入变量

选取影响客流分布的主要因素并将其量化后作为模型的输入变量。变量维数过多会给网络学习带来不必要的麻烦，并可能造成预测精度的下降；变量维数过少，神经网络难以发现样本的规律性。笔者采用5个影响因素作为系统的输入变量，如表1所示。

表1 系统输入变量及其标定方法

图3 GDFNN结构

在输入层，节点的个数为系统输入变量的个数，共有r个输入变量，每个输入变量xi(i= 1, 2,…,r)有u个隶属函数uij(j= 1, 2,…,u)。在隶属函数层，笔者采用高斯函数作为隶属函数，表示为：

(2)

输出层的输出是每一个输入信号的叠加。输出变量为

(3)

式中，ωj是结果参数或第j个规则的连接权。

1) 初始化系统预定义参数。

2) 输入第1个样本数据产生第1条模糊规则。

3) 输入新的样本数据，计算当前样本与所有模糊规则的马氏距离，找到最小值dmin，并计算实际输出误差ei。

4) 若满足dmin>kd，则转5)；否则转7)。其中,kd是与学习次数有关的设定值。

5) 若满足ei>ke，则产生新规则，并计算出所有规则的重要性η；否则转8)。其中，ke是与学习次数有关的设定值。

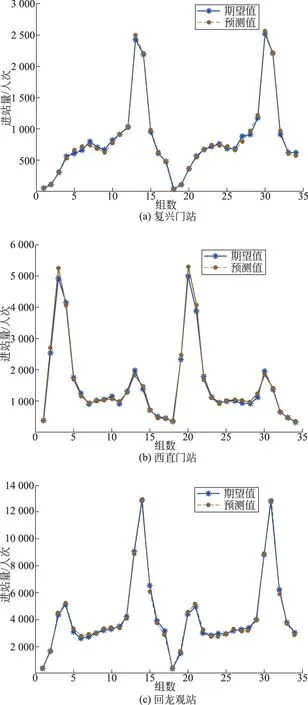
6) 若满足η

7) 若满足ei>ke，则调整高斯函数的宽度和结果参数；否则转8)。

8) 调整结果参数。

9) 观测是否完成，若仍有数据则返回3)，否则结束学习。

1) 根据影响客流分布的因素确定预测模型的输入变量。

3) 对训练完成的网络，使用测试数据测试网络的性能。

4) 使用预测数据进行预测，验证模型的有效性。

4 案例分析

4.1 样本数据选择与预处理

样本车站为：复兴门站(两线换乘站，进出站客流有明显潮汐特征)、西直门站(三线换乘站，交通枢纽)、回龙观站(早高峰进站客流大)。统计2013年9月20日至2013年12月27日每日各时段(以小时为单位)车站的进站量，进行实验。

训练数据：2013年9月20日到2013年12月19日分时段的进站量，共1 547个数据。

测试数据：2013年12月20日到2013年12月24日分时段的进站量，共85个数据。

预测数据：2013年12月25日到2013年12月26日分时段的进站量，共34个数据。

实验时，采用高斯函数作为隶属函数，其最佳使用范围为[0,1]。为避免原始数据过大造成网络麻痹，并提高网络泛化能力，需要对原始数据进行归一化处理后作为网络的输入(式4)，并对网络输出进行反归一化处理(式5)，得到预测值

(4)

Y(t)=y(t)(maxX(t)-minX(t))+minX(t)

(5)

式中,X(t)为原始数据，x(t)为网络输入，y(t)为网络输出，Y(t)为预测数据。

4.2 网络测试与训练

笔者对3个样本车站均进行了实验，以复兴门站为代表，对网络训练进行说明。随着样本数据的增加，模糊规则在不断变化，网络结构也随之动态调整，训练结束后共产生18条模糊规则，如图4所示。

图4 模糊规则产生与动态变化过程

图5为网络训练过程中的实际输出误差，从图中可以看出在训练初期网络不稳定，绝对误差值和变化幅度都较大(最大为2 000人次)，随着训练的进行，从第1 000组数据开始，误差维持在0至200之间，网络趋于稳定。

图5 网络实际输出误差

网络学习结束后，采用85个测试数据对网络进行稳定性验证。图6为测试数据的预测值和期望值对比图，从图中情况来看，期望值与预测值曲线拟合程度高。图7为相对误差图，最大相对误差值为8.00%，预测效果良好。

图6 测试数据结果对比

图7 测试数据相对误差

4.3 预测结果性能分析

预测结果如图8所示，预测值与期望值拟合程度较好。复兴门站预测值相对误差的绝对值最大为7.96%，最小为0.45%；西直门站预测值相对误差的绝对值最大为7.04%，最小为0.04%；回龙观站预测值相对误差的绝对值最大为7.25%，最小为0.36%。

图8 3座车站预测结果

表2 3种预测方法指标比较

5 结语

目前，由于训练数据仅包含两个月的日常进站客流数据和一年的节假日(十一假期)数据，数据样本量有限，导致模型预测的最大误差为8%，但随着进站客流数据的丰富，网络泛化能力加强，预测精度会进一步提高。

[2] 周开利, 康耀红.神经网络模型与其MATLAB仿真程序设计[M].北京:清华大学出版社，2005.

[3] 董升伟.基于改进BP神经网络的轨道交通 短 时 客 流 预测方法研究[D].北京:北京交通大学，2013.

(编辑：王艳菊)

Li Chunxiao1,2Li Haiying1Jiang Xi1Xu Xinyue1Zhao Aqun3

(1.State Key Laboratory of Rail Traffic Control and Safety, Beijing Jiaotong University, Beijing 100044;2.School of Traffic and Transportation, Beijing Jiaotong University, Beijing 100044;3.School of Computer and Science, Beijing Jiaotong University, Beijing 100044)

Directing against the characteristics of unbalanced, highly nonlinear and dynamic short-term entrance passenger flow of rail transit, the paper presents a short-term entrance passenger flow forecast method based on generalized dynamic fuzzy neural networks(GD-FNN), which combines the logical reasoning ability of fuzzy technology with the self-learning ability of neural networks. The paper determines the main factors affecting the distribution of short-term passenger flow by analyzing the features of passenger flow with the data of Beijing metro stations; and then a forecast model has been established by using GD-FNN to predict the short-term entrance passenger flow; finally, several stations in Beijing rail transit are used as numerical examples to confirm that this model can precisely approximate to the practical data (maximum relative error is less than 8%) and has good stability compared with traditional neural networks.

rail transit；generalized dynamic fuzzy neural networks；short-term passenger forecast；entrance passenger flow

李春晓，女，硕士研究生，从事城市轨道交通客流组织研究，14120844@bjtu.edu.cn

国家重点实验室自主课题(RCS2015ZZ002)

U293.6

A