多普勒与伪码相位值结合的A－GPS快速定位算法研究

黄志勇，赵冬青，田翌君，吴 昊，张爽娜

（1．信息工程大学 地理空间信息学院，河南 郑州450001；2．航天恒星科技有限公司（503所），北京100000）

常规GPS接收机自主冷启动的首次定位时间（TTFF）大约需要1 min，并且存在着在城市峡谷（ur ban canyons）等微弱信号条件下无法定位的问题［1］。辅助全球定位系统通过蜂窝网基站提供给A－GPS接收机捕获辅助信息、辅助星历、时间与概略坐标，解决了微弱信号下的定位问题［2］。由于A－GPS接收机预先就知道了所要搜索的卫星号、多普勒频移与码延迟，三维搜索空间被确定，减少了捕获和跟踪耗时，首次定位时间只需要数秒左右。此外，由于A－GPS接收机被设计的预先知道需要搜索哪个频率，接收机的结构变得允许进行更长的时间累积，从而增加了在每个特定的频率接收到的能量［1］。这增加了A－GPS接收机的灵敏度，并允许它捕获更弱的信号。

首次定位所需时间是指从接收机启动到给出第一个GPS定位结果所需的时间，它包括接收机对多个卫星信号的捕获、跟踪、位同步、帧同步、解码导航电文以及定位运算等一系列过程。当接收机处于室内等微弱信号环境时，由于导航电文解调比特错误率［3］（BER，Bit Error Radio）太高，接收机仅能通过跟踪过程获得跟踪环路中的伪码相位值与多普勒频移值，无法进行后面的位同步、帧同步以及解调导航电文［4］。由于接收机仅能测量部分的伪距，只能恢复部分的信号发射时间，而不能得到卫星在发射信号时的具体位置，该问题又被称作“粗时段导航问题”［1］。

GPS卫星距地面的远近不同，发射信号的传输时间在64～89 ms间变化，粗时段问题即我们只知道亚毫秒的伪距时，如何恢复全部的测量伪距来进行定位解算。针对该问题，Syrjarinne首先提出“时间恢复”［5］的概念，即利用辅助手段恢复完整的信号发射时刻，然而信号微弱时，由于检测互相关峰值的漏警率［6］太高，导致该方法难以实现；Sir ola改进了增强型三角测量法，提出了一种采用lambdafraction函数［7－8］消除卫星信号发射时刻模糊度的方法，然而当消除信号发射时刻模糊度时，使得接收机钟差等效距离的大部分也被消除了；Roland Kaniuth提出了一种Snapshot算法，但该算法存在整数毫秒模糊度问题［1］；Van Diggelen提出了一种重构全伪距［9］的解决粗时段导航问题的粗时定位算法来解决整数毫秒翻转的问题，然而该算法要求先验位置和时间误差小于0．5光毫秒。

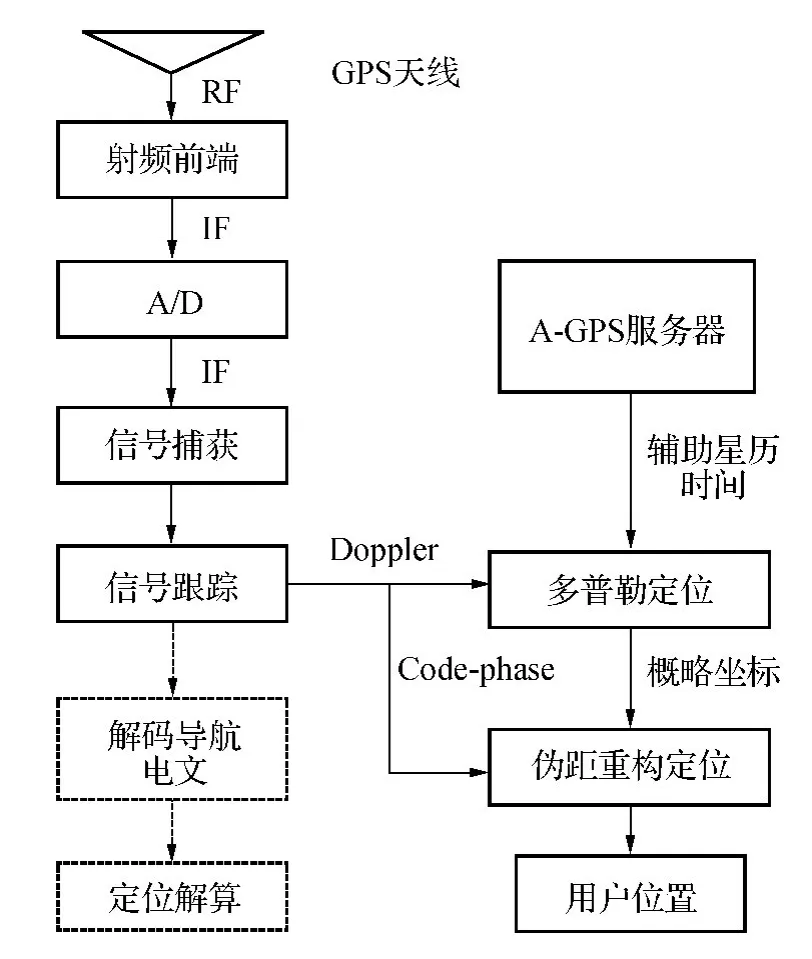
图1 多普勒与伪码相位结合的A-GPS快速定位算法研究流程

本文提出的多普勒与伪码相位结合的A－GPS快速定位算法，仅运用信号跟踪环路获得的多普勒频移和伪码相位值便可以快速获得定位结果，大大减少了TTFF［10］，其计算流程如图1所示。伪距重构算法通过A－GPS服务器提供的概略位置、时间与辅助星历，能够获得稳定的快速定位结果。然而当接收机处于离线模式时，无法得到概略坐标。基于多普勒频移测量值的定位结果虽然精度受限，却能为伪距重构算法提供概略坐标与时间，且总误差一般在150 k m以内。当接收机处于运动模式时，由多普勒值得到的定位结果误差较大，此时可以通过设置约束条件迭代计算，确保获得正确的重构的全伪距值。

1 算法基本原理

1．1 伪距重构算法

辅助GPS接收机大多数情况下没有精时间辅助（精时间辅助指优于10 ms精度的辅助时间，GSM、U MTS、WCDMA时间精度为1～2 s，CDMA时间精度为微秒级），此时，可以通过解码TOW来获得，但这需要耗费数秒的时间。而且在信号及其微弱的情况下，长时间亦无法解码星历，无法获得TOW。卫星的相对运动引起了粗时段导航的问题，可以计算每颗卫星的相对速度，运用导航方程去求解用户位置Xu（xu，yu，zu）和接收机公共偏差b以及粗时误差tc。即可以求出时间，而不依靠于解码得到它，这样也缩短了首次定位时间。

引入粗时误差tc，导航的4个步骤如下：

1）通过辅助星历与时间信息估计卫星的状态。

3）通过测量得到的伪码相位值zk，chip重构全伪距得到实际的伪距测量值ρ。

4）根据预测与实测伪距间的偏差，来调整先验状态，用δρ表示，δρ＝ρ－。因此，状态更新向量为δx ＝ ［δx，δy，δz，δb，δtc］T对先验状态x，y，z，b，tc更新的向量，而δρ中受到δtc的影响，且与δtc之间的关系为

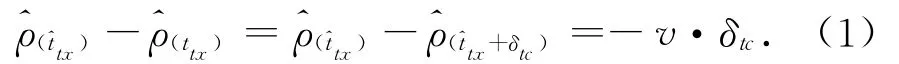
其中：ttx表示实际的发射时间。＾ttx表示对ttx的粗时估计。v＝（）是伪距速率。对于每颗卫星，δρ（k）和x之间的关系为

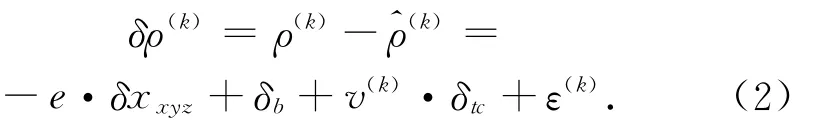
对于k颗卫星，可得到矩阵方程

因此，只要有5颗以上的卫星，就能得到粗时间辅助下的闭合五状态解。而构造先验残差时，由于亚毫秒伪距测量值（即伪码相位测量值）zk，chip存在未知的公共偏差b（主要是接收机钟差）和测量误差ε，卫星到接收机的真实几何距离期望为r，伪距中存在先验的位置和时间误差rd，当未知的公共偏差和期望伪距的结合接近1 ms时，取模运算容易出现1 ms的偏转情况。令z为亚毫秒伪距值的真值，则

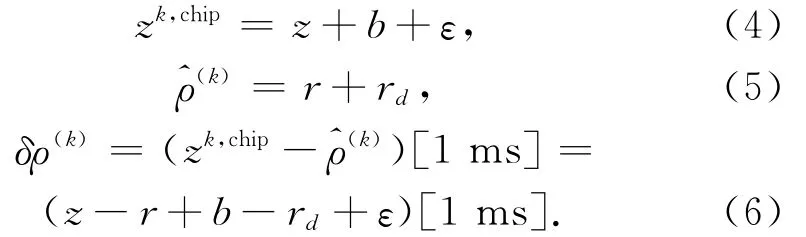
针对上述算法存在整毫秒模糊度问题，可以用选定参考星使其含有相同的误差项的办法解决。用上标（0）来表示参考卫星，用（k）表示其他卫星。计算所有卫星的期望伪距，并根据参考卫星的期望伪距值给参考卫星赋整数值N（0），故其全伪距为（N（0）＋z（0））ms。几何距离中含有由先验位置和时间误差引起的误差r（0）d，重构的全伪距与几何距离r（0）的关系为

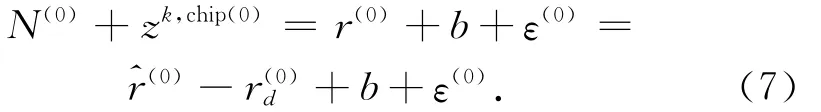
如果对所有测量值指定一个整数值，使它们含有相同的公共偏差，则对于卫星k会得到以下的方程：

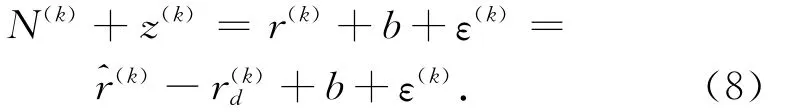
由于它们含有相同的公共偏差，两式相减，得

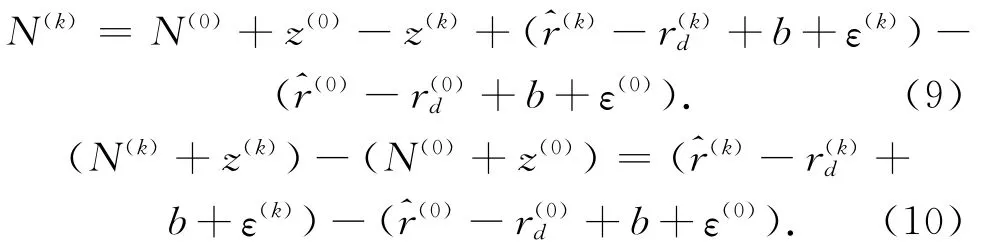
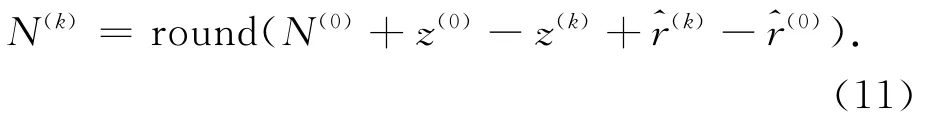
1．2 多普勒定位算法

前面已经推导了伪距线性导航方程，式（3）两边对时间微分，得

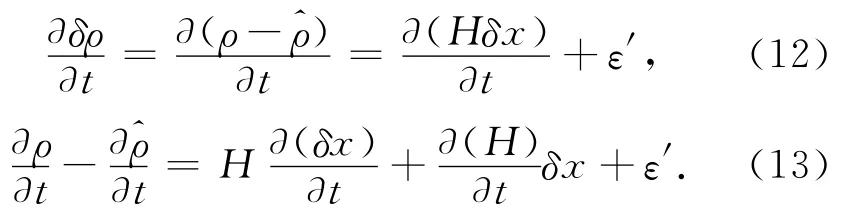
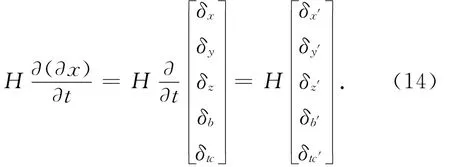
其中：δx′δy′δz′为接收端先验速度状态的更新状态；δb′为先验频率偏移的更新状态；δtc′为先验粗时误差更新状态。第2项多普勒测量值和位置更新状态之间的关系为

三维向量［∂e（k）／∂t］与［∂v（k）／∂t］的表达式如下：

其中：X（k）s为卫星k的位置，Xu为接收机的先验位置信息。省略上标（k），并用变量r代表卫星与接收机的距离，r＝｜Xs－Xu｜。

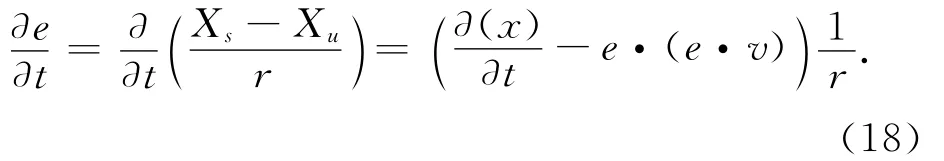
将式（15）、式（16）和式（18）代入式（13）可得

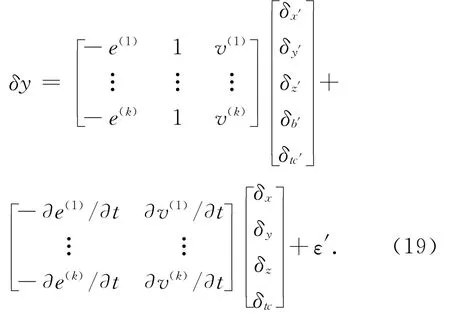
式（19）即为包含9个状态（3个接收机位置、3个速度、频率偏移、粗时误差、粗时误差变化率）的关于瞬时多普勒测量值的线性方程。如果接收机端是静止的，且忽略粗时误差变化率，那么式（19）的未知量减少到5个，因此可以由5颗卫星的多普勒测量值得出接收机端的位置。

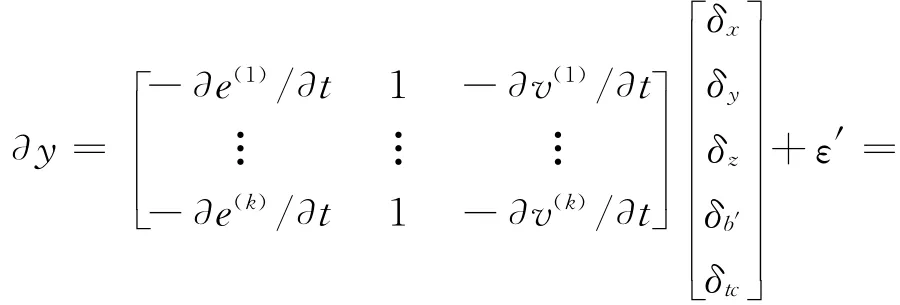
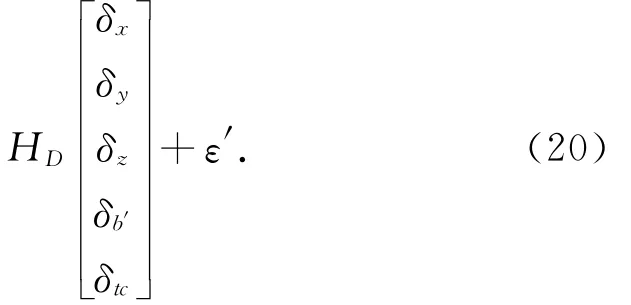
式（20）的最小二乘结果为

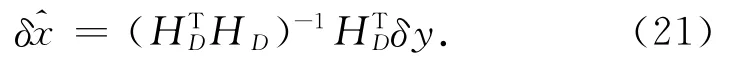
当上式定位误差小于100 k m时，时间误差小于1 min时，可以成功地为伪距重构算法提供概略坐标与时间，特殊条件下不能满足时，通过设置约束条件进行迭代计算可以很快地固定正确的整数毫秒模糊度。

1．3 基于多普勒定位算法的约束条件

由以上推导可知，当多普勒定位提供的定位总误差小于0．5光毫秒时，重构全伪距算法能够得到正确的定位结果。当不能满足时，可以设置如下的两个约束条件。

1．3．1 粗时误差约束条件

GPS卫星的位置和速度实际上是与时间相关的函数，由于没有完成解码导航电文，没有解码出TOW（周内时），不能获得准确的信号发射时间。当有蜂窝网的时间辅助时，一般能满足定位要求。在处于离线模式时，粗时误差较大，可能导致较大的卫星位置和速度误差。这时可以通过约束条件，每1 s计算一个多普勒残差值，使得多普勒残差值为最小的备选时间即为所求。

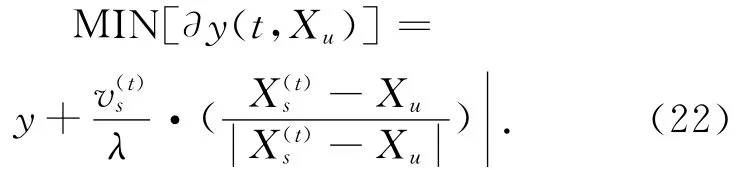
上式中，Xu只需满足用户位置到地球质心的距离Xr与地球半径R之差不超过200 k m，地球上任意概略坐标均能满足此要求，即

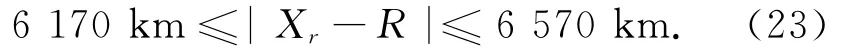
1．3．2 整数毫秒模糊度约束条件

当接收机以较高的速度移动时，基于多普勒定位获得的概略坐标误差可能大于150 k m，此时存在整数毫秒模糊度的问题。可以通过模糊度搜索法解决该问题，由于1 ms的伪距值为150 k m，模糊度搜索空间一般很小，一般每颗卫星进行数次搜索便能获得正确的伪距值。

若每颗卫星搜索3次，可见卫星为8颗时，总的搜索次数为38次。使概略坐标改正数最小的备选整数毫秒值N即为所求。此时要求粗时误差不超过1 s，使用普通的时钟一般能满足精度要求。

1．4 数据解算流程

由以上所述可知，多普勒与伪码相位值结合的A－GPS快速定位算法的解算流程如下：

步骤1：设备从参考接收机或者A－GPS位置服务器获得辅助星历（在离线模式下使用扩展星历（Ephemeris Extension，EE）），从而知道了当前可见卫星的方位、仰角等信息。

步骤2：A－GPS接收机通过辅助星历快速捕获卫星，进行伪码相位与多普勒频移测量。

步骤3：运用多普勒值进行初始定位，为伪距重构算法提供一个概略坐标与时间。

步骤4：运用伪距重构算法，得到完整的伪距观测值，与预测的粗几何距离作差得到伪距残差，迭代求解五状态方程［11－12］。

步骤5：构造一个位置的后验残差统计量，当正确解算出全伪距时，后验残差的值很小，反之很大。可以通过上面的两个约束条件来重新进行多普勒定位与整数毫秒模糊度搜索，如果仍不能正确解算，则需要调整先验概略坐标与时间，返回步骤3，直至求解出正确解。

2 实验数据分析

为了验证该算法的有效性，选取IGS参考站德国PTBB站（布伦瑞克，其真实空间直角坐标为（3 844 059．913 5，709 661．370 0，5 023 129．594 5））2013年5月27日的300个历元的定点观测结果进行仿真验证。在仿真计算时，使用真实伪距观测值取整得到亚毫秒伪距（伪码相位）值，运用真实的最终多普勒观测值代替跟踪过程中获得的多普勒频移值。

首先运用多普勒值进行定位计算，使粗时误差为1 s，并任意给定地球上一概略坐标，计算表明，经过数次迭代均能得到有效收敛。将其作为伪距重构算法的初始概略坐标，得到多普勒定位与伪距重构的A－GPS快速定位算法的三维位置RMS统计表（见表1）。另外，将300个历元的多普勒定位与伪距重构定位算法的3个方向的位置误差曲线图绘制如图2、图3所示。

表1 多普勒定位与伪距重构定位算法的三维位置RMS m

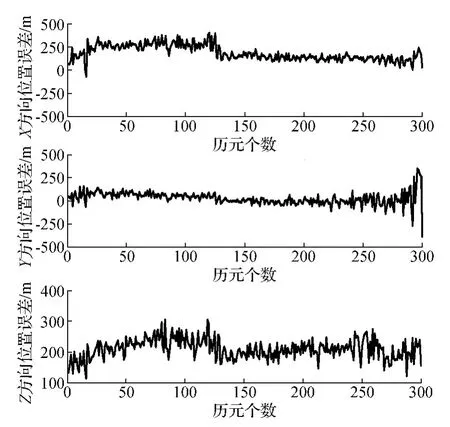
图2 多普勒定位3个方向的位置误差曲线

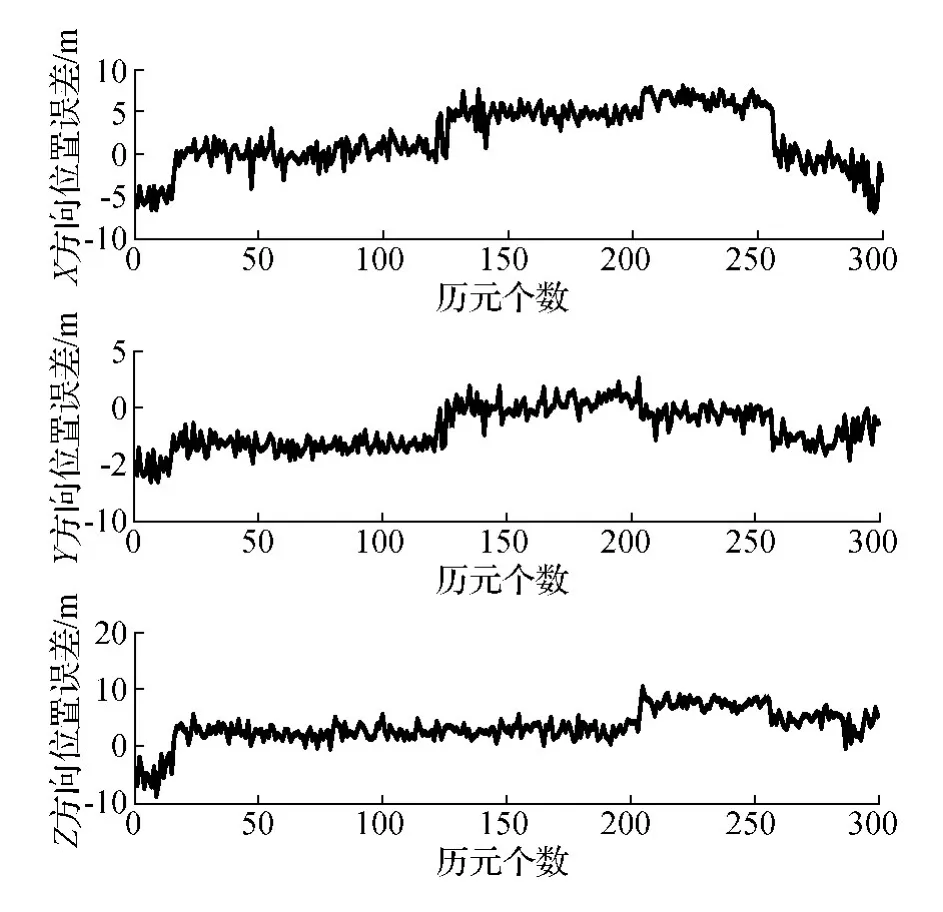
图3 伪距重构A-GPS定位算法3个方向的位置误差曲线

3 结束语

微弱信号环境卫星定位技术已成为了国际导航界研究的热点技术，其中将GPS定位技术与无线通信平台相结合发展A－GPS定位系统被认为是最具应用前景的研究方向之一［2］。辅助GPS能大大扩展传统GPS的使用范围，并且能大大缩短首次定位时间（TTFF）。

本文提出的多普勒与伪码相位值结合的AGPS快速定位算法能够应用于传统GPS无法涉足的微弱信号领域。该算法只需要对GPS信号完成伪码相位和多普勒频移测量，无需完成位同步、帧同步和解调导航电文。本文给出了多普勒定位与伪距重构算法的计算流程，推导了基于多普勒定位的A－GPS快速定位算法的约束条件，并利用仿真数据验证了该算法的可行性。验证表明，多普勒定位算法无需初始坐标，定位精度为200 m左右，能够为伪距重构算法提供可靠的初值。伪距重构算法定位精度优于10 m，接近于传统GPS定位算法。

随着基于位置服务需求的增长与我国北斗卫星导航系统的迅速发展，自主研究辅助北斗卫星导航系统（A－BDS）的需求更加迫切，本文提出的算法或可以有效地应用到辅助北斗卫星导航系统当中。

［1］ （南非）迪格伦．辅助GPS原理与应用［M］．孟维晓，马永奎，高玉龙，译．北京：电子工业出版社，2013．

［2］ 宋成．辅助型GPS定位系统关键技术研究［D］．长沙：国防科学技术大学，2009：135－138．

［3］ 谢钢．GPS原理与接收机设计［M］．北京：电子工业出版社，2009：266－270．

［4］ 米斯拉，恩格．全球定位系统—信号、测量与性能［M］．罗鸣，译．北京：电子工业出版社，2008．

［5］ SYRJARINNE J．Studies of Modern Techniques for Personal Positioning［D］．Ph．D dissertation，Tampere：Tampere University of Technology，2001：43－47．

［6］ SYRJARINNE J．Possibilities f or GPS ti me recover y with GSM net work assistance ［C］Proc．ION GPS，2000：2－4．

［7］ SIROLA N．A Met hod for GPS Positioning Without Current Navigation Data［D］Master of Science dissertation，Tampere：Tampere University of Technology，2001：45－49．

［8］ AKOPIAN D，SYRJARINNE J．A net wor k aided iterated LS method f or GPS positioning and time recovery without navigation message decoding ［C］．PLANS 2002，Pal m Springs，CA：77－84．

［9］ FRANK VAN DIGGELEN．Method and apparatus for computing position using instaneous Doppler measurements from satellite ［P］． U． S． Patent 7987048B2．2011：1－5．

［10］CHEN H W．A new coarse－ti me GPS positioning algorith m using co mbined Doppler and code－phase measurements［J］．GPS Solutions 2013，10（22）：5－7．

［11］陈陌寒，巴晓辉，王云，等．辅助式GPS接收机的快速定位算法研究［J］．科学技术与工程，2011，11（10）：2220－2224．

［12］邱蕾，刘正平，伍岳，等．GPS现代化后LS载波的数据质量分析［J］．测绘工程，2015，24（2）：6－9．