基于改进Cao算法确定奇异谱嵌入维数及应用

岳 顺，李小奇，翟长治

（1．河海大学 地球科学与工程学院，江苏 南京210098；2．河海大学 水利水电学院，江苏 南京210098）

我国自20世纪90年代起，在一些大型重要桥梁上均建立了不同规模的健康监测系统，在这些桥梁关键部位均布设有GPS监测点，由于监测点变形的错综复杂性，变形监测序列可能包含各种各样的误差与变形信息，必须通过对监测数据进行综合处理分析，提取变形信息，发现变形规律。因此，针对不同桥梁的特点，在其运营期进行变形监测和养护维修，通过对监测数据的处理与分析，挖掘提取结构变形特征，分析评定结构安全状态，对潜在的结构和功能危险进行预警，对确保桥梁的安全，减少灾害的发生具有十分重要的意义［1］。

基于主分量的奇异谱分析（singular spectr u m analysis，SSA）作为数字处理技术早已被广泛应用，SSA的功能是对于原序列隐含的波形信号从它的含噪声的有限长观测系列中提取。但是由于奇异谱分析嵌入维数（Embedding Di mension），也称窗口长度，大多数人是靠经验或者交叉验证的统计方法来确定最佳的嵌入维数。但是这些方法具有很强的主观性，缺乏实质性的分析，而由Cao Liangyue提出的Cao算法，由于其算法简捷，易于实现，且实用性强，因此获得广泛的应用。本文基于Cao算法来确定SSA嵌入维数，并通过仿真实验，验证其可行性，最终通过SSA对苏通大桥索塔GPS的监测序列进行分析，得到较好结果。

1 Cao算法

Cao算法具有对数据长度依赖不强，能清楚地区分真实信号和噪声，以及计算效率高等优良特性［2－3］。首先，根据式（1）计算相空间中的点在各嵌入维数条件下的最近邻点的距离变化值。

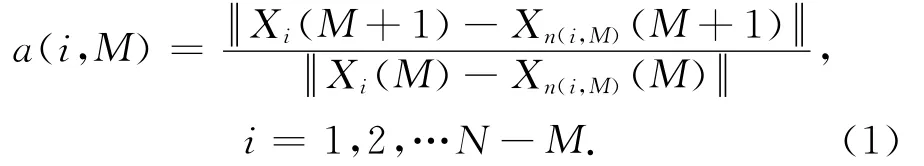
其次，根据式（2）计算相同维数下距离变化值的平均值。

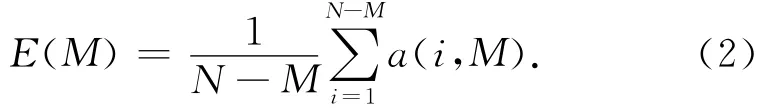
式中：E（M）为所有a（i，M）的均值。最后，根据式（3）检测E（M）的变化情况。

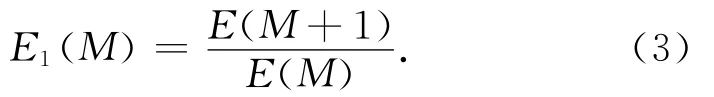
若当M＞M0时，E1（M）停止变化或变化波动较小，那么最小嵌入维数为M0＋1。

2 改进的Cao算法

Cao算法存在的问题是：在确定嵌入维数M时，是依据E1（M）停止变化为标准，但并没有给出判断停止变化的准则，仅依靠主观判断，而实际时间序列E1（M）是经常有起伏的，很少出现严格意义上的停止变化，这给M的确定带来困难。针对上述问题，本文对Cao算法提出改进，提出嵌入维数的稳定性准则，计算步骤如下：

1）计算：

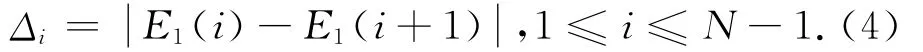
2）可根据E1的波动情况选取一个阈值e，找到第一个Δi＜e对应的下标u，计算：

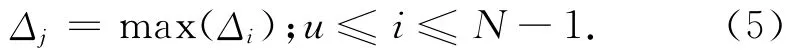
3）重新设置：

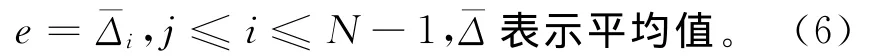
4）取j≤i≤N－2，当Δi＞Δi＋1且Δi＋1＞Δi＋2且Δi＋1＜e时，嵌入维数M＝i＋1。

3 SSA原理

SSA是在Karhu men－loeve分解理论的基础上形成的[4]，对象是经过中心化的一维时间序列｛xt，t＝1，2，… ，N ｝，N表示时间序列长度。它可以从含噪声数据序列中提取具有显著周期振荡行为的信号分量，并有效利用周期分量重建序列的预测技术，通过提炼数据主要成分，过滤掉非周期性的异常噪声，达到降噪的目的［5］，进而得到序列变化的趋势。SSA计算步骤如下：

3．1 确定嵌入维数M

把时间序列时延地排列成M阶迟延矩阵

其中：

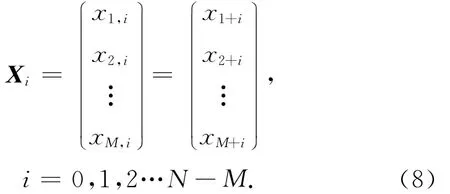
它称为X的第i个状态向量，共有N－M＋1个状态［6］。

3．2 计算X的协方差矩阵S x

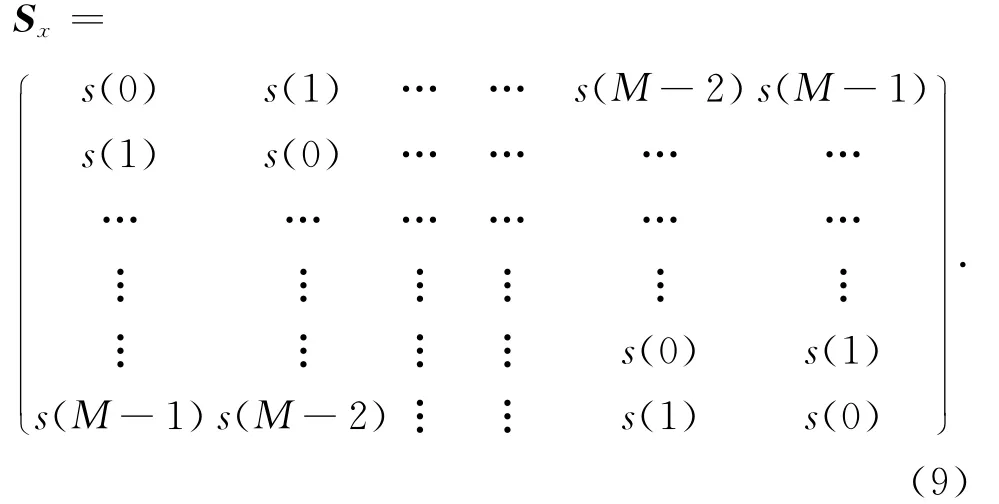
其中：

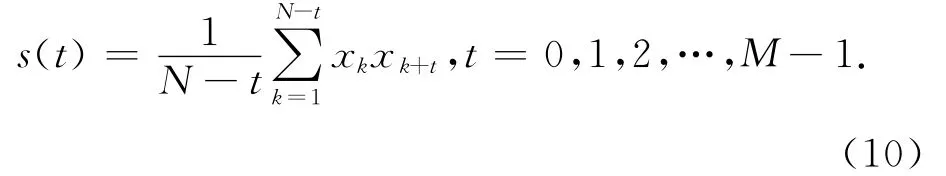
s（t）为时间序列迟后为t的自协方差，0≤t≤M－1。Sx的特征向量Ek反应时间序列x中的时间演变型，在SSA中称为T－EOF，另外

称为时间主成分（T－PC）。

3．3 重建成分

SSA最重要的应用是重建成分Rc（Reconstr uction），利用第k个T－EOF和T－PC重建成分ykt，则

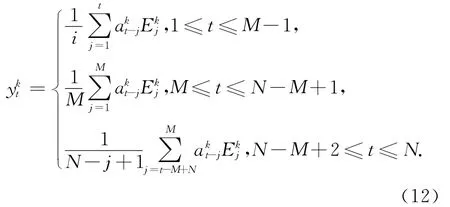
原序列可以表示为所有重建成分的和，为

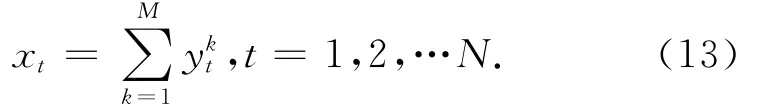
但在实际应用中通过使两个指标，即噪声残余能量指标和信号畸变指标［7］同时达到最小来确定主分量的截断位置，即p之所在。选取前p个具有显著波形或周期分量重建原序列为

在SSA分解的基础上重建分量序列，从而研究重建分量的长期变化特征。

4 仿真实验

采用加噪序列

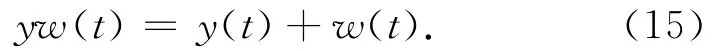
它由原序列为

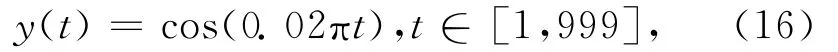
和随机噪声w（t）组成，实验前进行数据中心化，根据式（1）、式（2），随着 M 的增大计算出式（3）的值，得到图1。

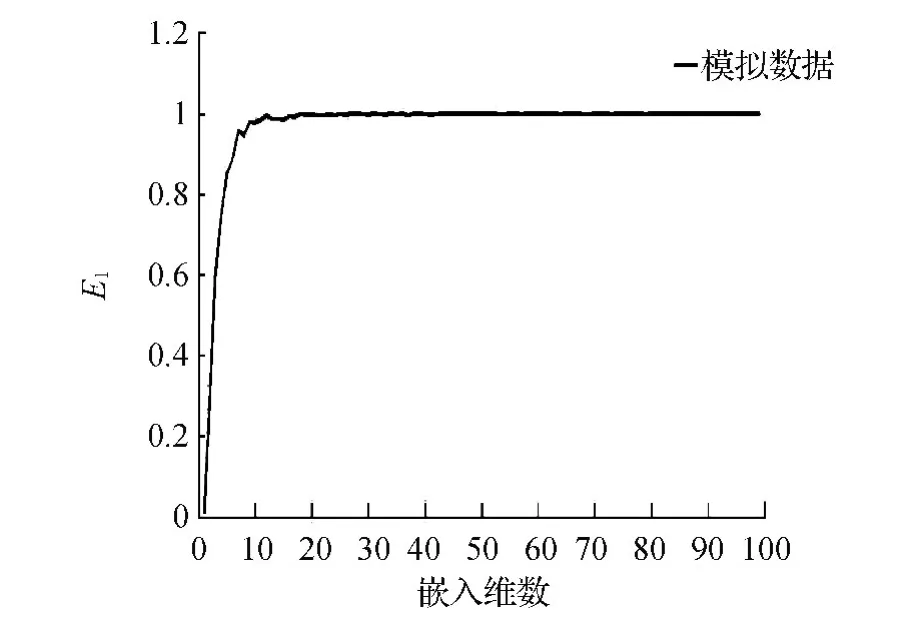
图1 仿真序列嵌入维数与E 1的关系

从图1可以看出，当M＝20时，E1开始稳定下来，但有些波动，这些波动对确定嵌入维数造成一定的影响，根据图1的E1的波动情况，选取e＝0．0001利用改进的Cao算法可以解决这个问题，求出嵌入维数M＝42，然后利用求的嵌入维数对仿真序列进行SSA。为了突出SSA的效果，把当M＝20、M＝42时的原始序列、加噪序列和奇异谱分析后重建序列画出来，得到图2、图3。

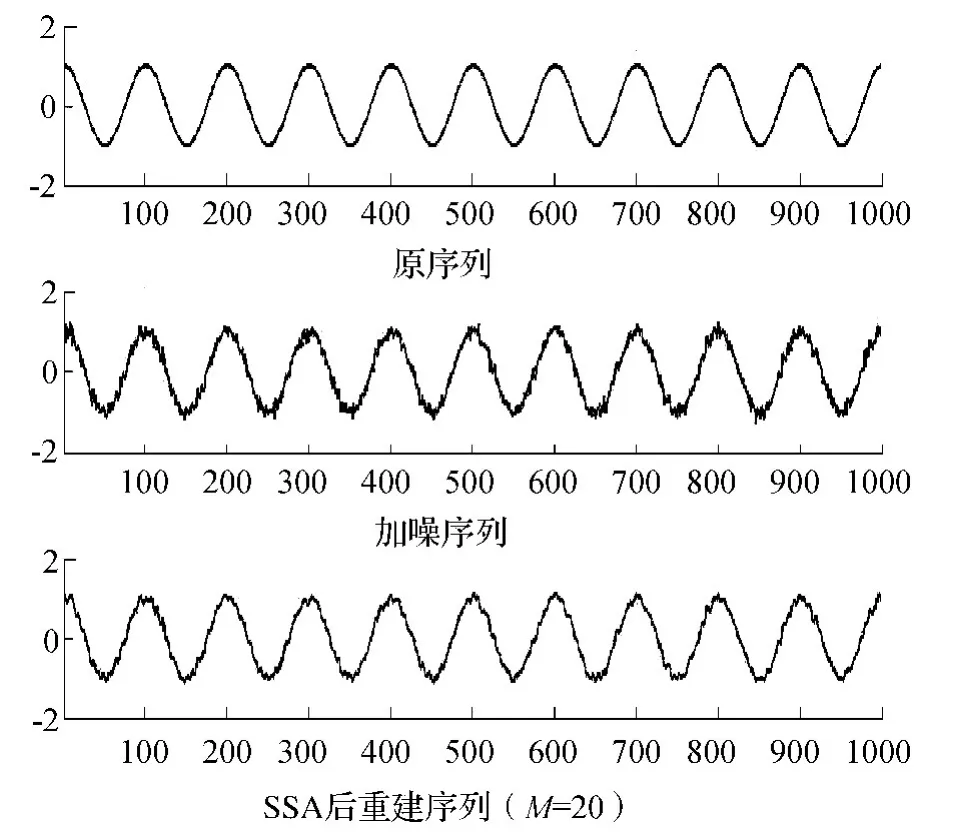
图2 M＝20时仿真原序列、加噪序列和SSA分析后重建序列分布情况

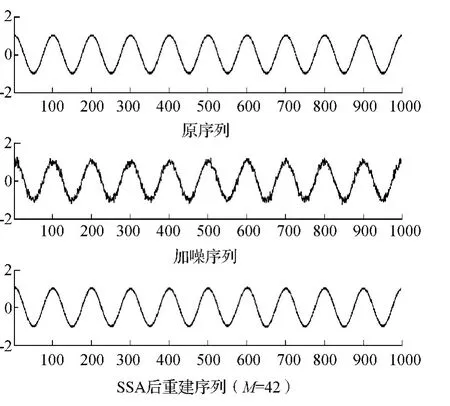
图3 M＝42仿真原序列、加噪序列和SSA后重建序列分布情况

从图2、图3中，当M＝42时，SSA重构序列较平滑，为了定量表示去噪的效果，引入平滑度系数r，其中

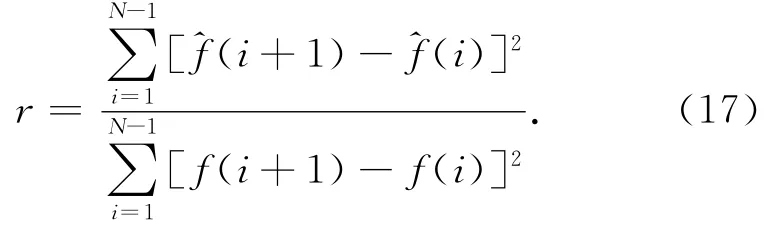
式中：f（i）表示原始序列；＾f（i）表示 SSA 去噪后重建序列；N表示序列长度，平滑度系数越小，表示去噪效果越好。当M＝20 M＝42时分别求出r为r20＝0．1801，r42＝0．0012，基于改进的 Cao得到的平滑度系数较小，说明改进的Cao算法具有较高的平滑度，去噪效果更好。经过重建序列，原始时间序列中的主要趋势成分和振荡周期得到有效提取，噪声干扰项明显降低，说明基于改进的Cao算法能够很好地确定嵌入维数，其对接下来的变形监测数据处理将提供帮助。

5 监测数据处理

索塔是斜拉桥关键的工程部位，因为索塔不仅要承担它本身的重量，还要承载全桥的荷载。因此，监测与分析桥梁索塔的动态特性，包括变形幅度、振动的频率、趋势，可为确定桥梁索塔状态提供可靠的科学依据。GPS对索塔的变形监测是随着时间进行的，可以看成是一种时间序列。奇异谱分析是可以较好地从含噪声的有限尺度时间序列中提取信息，目前已应用于多种时间序列的分析中［8］。

监测数据选自2012年3月1号0时到3月7号0时的7 d的苏通大桥索塔监测数据，采样周期是5 min，首先进行数据中心化。苏通大桥索塔变形监测分为3个方向：X，Y，Z。分别对X，Y，Z 3方向运用改进Cao算法得到的嵌入维数M与E1的关系图，如图4～图6所示。

图4 X方向嵌入维数与E 1的关系

从图4～图6中可以看出随着嵌入维数M的增大，X，Y，Z趋于稳定，但是有点波动，基于改进的Cao算法求解嵌入维数，得到3个方向的嵌入维数分别为45、47、92。利用得到的嵌入维数，对监测时间序列进行SSA，并做变形趋势拟合，得到图7～图9。

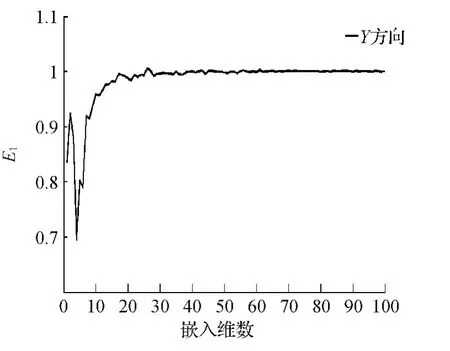
图5 Y方向嵌入维数与E 1的关系

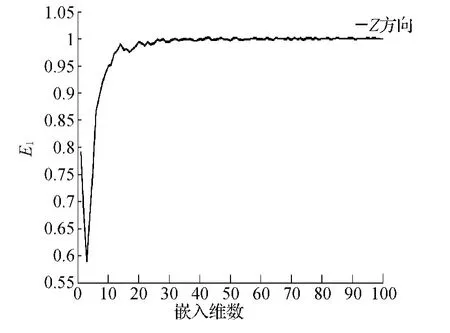
图6 Z方向嵌入维数与E 1的关系

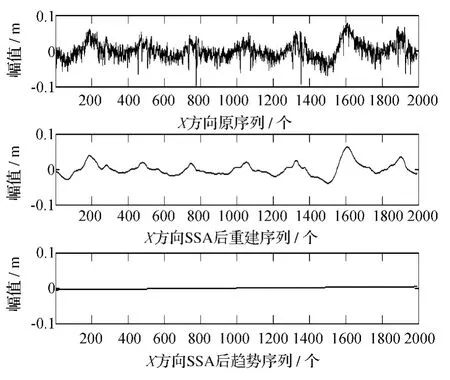
图7 X方向SSA前后序列及趋势项序列的分布情况

根据式（17），求得X，Y，Z 3方向的平滑度系数分别为rx＝0．0007，ry＝0．0009，rz＝0．0083，三者的平滑度系数都很小，说明SSA对3方向序列有着显著去噪效果。从图7～图9中X，Y，Z 3方向重构序列表现的比原序列光滑，没有出现明显锐角变化情况，具有显著降噪的功能，其基本上反映原始序列的波动变化，较好地捕捉到原始序列的趋势项。另外可以看出索塔在X方向的波动范围比Y，Z方向大，而且具有一定的周期性，周期约为1 d，从X方向SSA后重建序列可以看出当白天温度变化剧烈时，索塔混凝土膨胀收缩的较剧烈，索塔的变形量也同时变化显著，晚上温度变化缓慢，索塔混凝土膨胀收缩较平缓，索塔的变形量也跟着变化缓慢，但是索塔变形总能回到平衡位置，这与一天的温度变化相符合，说明温度对索塔有一定的影响，从整体的变形趋势可以看出3方向的变形都趋于稳定状态，说明大桥处于良好的工作状态。

图8 Y方向SSA前后序列及趋势项序列的分布情况

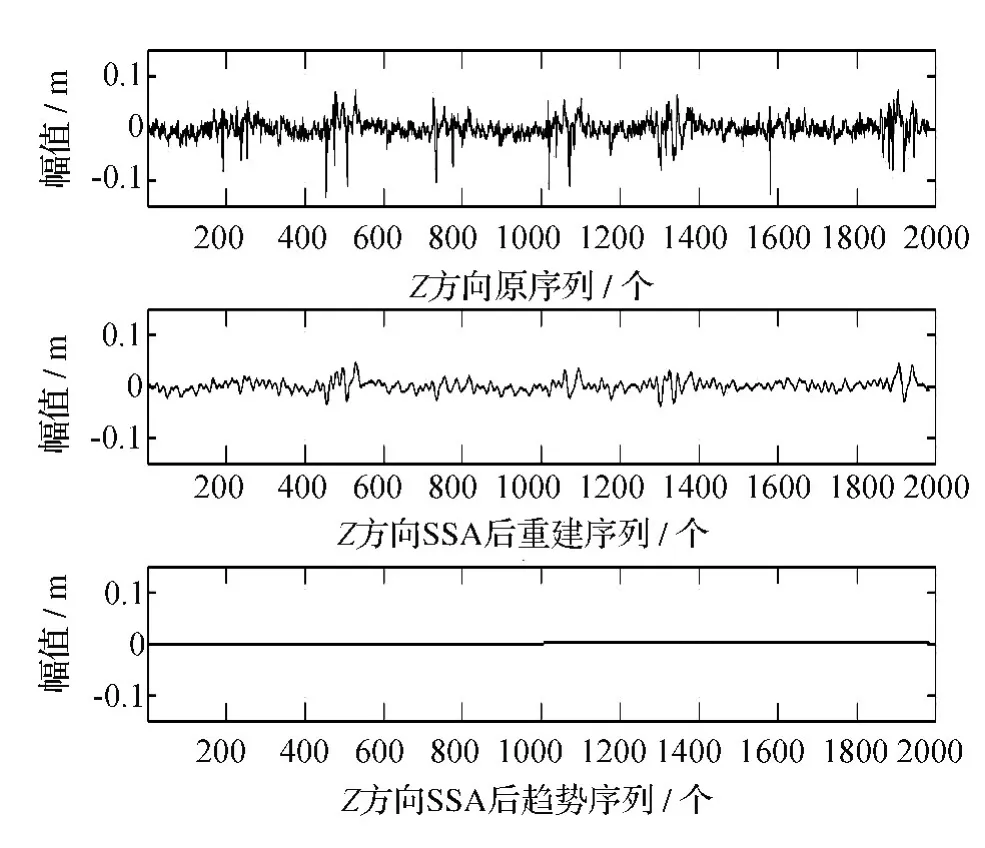
图9 Z方向SSA前后序列及趋势项序列的分布情况

6 结束语

根据上述分析，本文针对奇异谱分析时间序列嵌入维数存在主观性问题，提出基于Cao算法确定嵌入维数，同时对算法存在的不足，提出了改进。通过仿真试验，证明改进的Cao算法具有很好的准确性、稳定性及实效性，可以为奇异谱分析时间序列提供良好的基础，最后将其应用到GPS变形监测数据上，表现其对GPS数据的显著的降噪能力。分析温度对索塔变形的影响，本文仅从外部GPS变形监测序列进行分析，但是具体索塔内部影响因子对索塔变形的影响还需进一步探索与研究。

［1］ 陈亮，黄腾．基于灰色关联分析的卡尔曼滤波在桥梁变形监测中的应用［J］．测绘工程，2010，19（4）：47－49．

［2］ 韩敏．混沌时间序列预测理论与方法［M］．北京：中国水利水电出版社，2007．

［3］ 臧妻斌，黄腾．时间序列分析在地铁变形监测中的应用［J］．测绘科学，2014，39（7）：155－157．

［4］ 伍龙，邢丽坤，陈帅．基于奇异谱分析的最优分解层数确定 算 法 ［J］．计 算 机 工 程 与 应 用，2012，48（36）：137－141．

［5］ 刘元峰，赵玫．基于奇异谱分析的混沌序列降噪［J］．上海交通大学学报，2003，37（5）：778－780．

［6］ 施能．气象科研与预报中的多元分析方法［M］．北京：气象出版社，2002．

［7］ 孟建，屈梁生．基于主分量分析的噪声压缩技术［J］．信号处理，1998，14（4）：381－324．

［8］ 王解先，连丽珍，沈云中．奇异谱分析在GPS站坐标监测序列分析中的应用［J］．同济大学学报：自然科学版，2013，41（2）：282－288．