矩阵翻转法求解旅行最佳路线问题
2015-03-27申合帅段宝娜
申合帅, 段宝娜
(郑州财税金融职业学院 基础部,河南 郑州 450000)
矩阵翻转法求解旅行最佳路线问题
申合帅, 段宝娜
(郑州财税金融职业学院 基础部,河南 郑州 450000)
利用矩阵翻转法实现二次逐次修正求最佳哈密尔顿圈(H圈),这种方法编程容易,计算速度快,特别适用顶点数目较多的情况.
最佳巡回路线;矩阵翻转法;二次逐次修正法
1 问题的重述
某人准备出去旅行,计划走遍全国省会城市、直辖市、香港、澳门、台北.现按下面要求制订出行方案:①按经纬度设计最短旅行方案;②从哈尔滨出发,每个城市停留3天,可选择航空、铁路(快车卧铺或动车),设计最经济的旅行订票方案;③要考虑省钱、省时又方便.
2 模型的假设与符号说明
假设:①旅行中能准时乘坐火车或飞机;②在每个城市停留时,不会耽误时间;③在选定的交通工具下,价格与行程成正比r,所花费的时间也与路程成正比q.
符号说明:34个城市(哈尔滨、北京、上海、天津、重庆、长春、沈阳、呼和浩特、石家庄、太原、济南、郑州、西安、兰州、银川、西宁、乌鲁木齐、合肥、南京、杭州、长沙、南昌、武汉、成都、贵阳、福州、台北、广州、海口、南宁、昆明、拉萨、香港、澳门)分别标记为V1,V2,…,V34.Wij表示从i城到j城的距离,Fij表示从i城到j城的费用.
3 问题的分析
首先建立一张全国省会图,其中节点表示省会,边上的权表示代价,设其为N(V,E,W),V是节点集合,E为边的集合,W为边上的权,得到一个关于全国省会城市的完备加权图.所求问题就是求从哈尔滨所在的节点出发,巡回各节点的最短路,这个问题类似于TSP (traveling salesman problem,旅行商问题).
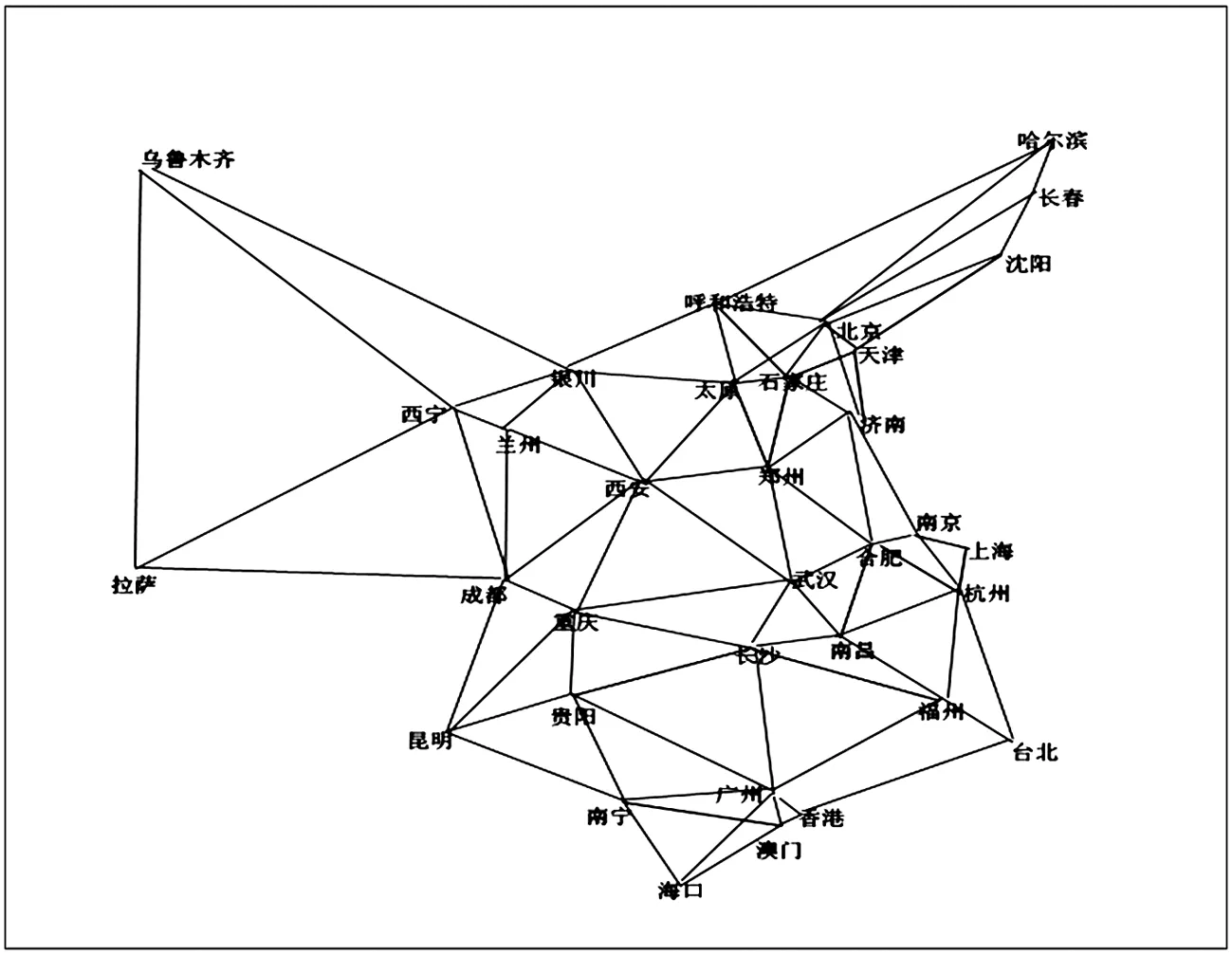
图1 全国省会城市图Fig.1 The chart of the national capital cities
4 模型的建立与求解
通过查找数据,得到各个省会城市、直辖市、香港、澳门、台北之间的最短距离(球面距离).利用Photoshop软件画出这34个城市之间的简略关系(图1).要求的最短旅行方案,是求最优哈密尔顿圈的问题[1].因此先给出一个近似的哈密尔顿圈,再利用矩阵翻转实现二次逐次修正法求得最优H圈.
矩阵翻转法[2]:在一个矩阵中,对第i列到第j列翻转,就是以i列和j列的中心位置为转轴并旋转180度.即第i列和第j列的位置互换,第i+1列和第j-1列位置互换;同理,行也适用.
二次逐次修正法[2]:
1) 任取初始H圈:C0=V1,V2,…,Vi,…,Vj,…,Vn,V1;
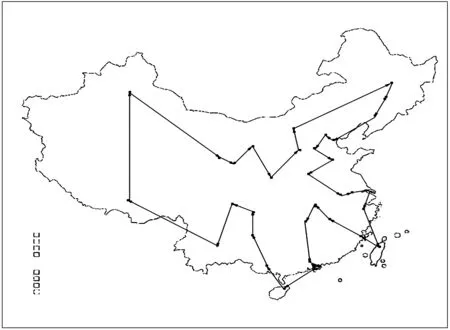
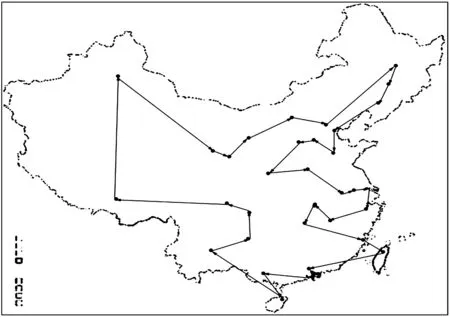
2)对所有的i,j, 1 C1=V1,V2,…,Vi,Vj,…,Vi+1,Vj+1…,Vn,V1; 3)对C重复步骤2),直到条件不满足为止,最后得到的C即为所求. 综上所述,用矩阵翻转法在完备加权图中寻求最佳H圈的整个过程如下[2]: STEP 1 在一个完备加权图中,任取初始H圈:C0=V1,V2,…,Vi,…,Vj,…,Vn,V1,按此点顺序可组成一个距离矩阵A=(aij)(n+1)×(n+1),其中 STEP 3 在距离矩阵A中,对所有的i,j,2 我们给出的起始旅行路线是:V1→V2→V3→V4→V5→V6→V7→V8→V9→V10→V11→V12→V13→V14→V15→V16→V17→V18→V19→V20→V21→V22→V23→V24→V25→V26→V27→V28→V29→V30→V31→V32→V33→V34→V1. 经过多次矩阵翻转优化运算,得到最优H圈是:V1→V6→V7→V4→V2→V9→V11→V12→V18→V19→V3→V20→V27→V26→V22→V23→V21→V28→V33→V34→V29→V30→V25→V5→V24→V31→V32→V17→V16→V14→V15→V13→V10→V8→V1. 最短的旅游线路,即哈尔滨→长春→沈阳→天津→北京→石家庄→济南→郑州→合肥→南京→上海→杭州→台北→福州→南昌→武汉→长沙→广州→香港→澳门→海口→南宁→贵阳→重庆→成都→昆明→拉萨→乌鲁木齐→西宁→兰州→银川→西安→太原→呼和浩特→哈尔滨.如图2,其行程的最小路程为:W=W1,6+W6,7+W7,4+W4,2+W2,9+W9,11+W11,12+W12,18+W18,19+W19,3+W3,20+W20,27+W27,26+W26,22+W22,23+W23,21+W21,28+W28,33+W33,34+W34,29+W29,30+W30,25+W25,5+W5,24+W24,31+W31,32+W32,17+W17,16+W16,14+W14,15+W15,13+W13,10+W10,8+W8,1=15 631.41 km. 在该问题中,给出的距离数据是城市间的航空距离,这与实际旅行中选择的方案有很大差距.因为出于经济和地理原因,我们会选择乘坐火车,而火车轨道的铺设不全是直接、笔直的,这就造成实际行程会比前面假设要大得多,因此,我们对数据进行完善.考虑经济因素,我们偏重于选择动车火车组作为主要旅行工具,在火车无法到达的地方,则选择乘坐飞机. 给出相同的起始旅行路线,经过多次矩阵翻转优化运算,得到最优H圈是:V1→V6→V7→V4→V11→V9→V10→V13→V12→V18→V19→V3→V20→V22→V23→V21→V26→V27→V28→V33→V34→V30→V29→V31→V25→V5→V24→V32→V17→V14→V16→V15→V8→V2→V1. 制定出的旅行路线为:哈尔滨→长春→沈阳→天津→济南→石家庄→太原→西安→郑州→合肥→南京→上海→杭州→南昌→武汉→长沙→福州→台北→广州→香港→澳门→南宁→海口→昆明→贵阳→重庆→成都→拉萨→乌鲁木齐→兰州→西宁→银川→呼和浩特→北京→哈尔滨(图3). 其行程的最小路程为:W=W1,6+W6,7+W7,4+W4,11+W11,9+W9,10+W10,13+W13,12+W12,18+W18,19+W19,3+W3,20+W20,22+W22,23+W23,21+W21,26+W26,27+W27,28+W28,33+W33,34+W34,30+W30,29+W29,31+W31,25+W25,5+W5,24+W24,32+W32,17+W17,14+W14,16+W16,15+W15,8+W8,2+W2,1=20 020 km. 对该路线的路费进行估算.总行程为20 020 km,其中除W26,27,W27,28,W30,29W29,31,W32,17路段不得已必须乘坐飞机外,其他路段选择火车最为经济,火车票价与路程的关系r设为0.308元/km,乘飞机的总路程为4 452 km,总票价为 2 680元,乘坐火车的路程为15 568 km,总火车票价为4 795元,总票价为7 475元.其行程的最小路费为:F=F1,6+F6,7+F7,4+F4,11+F11,9+F9,10+F10,13+F13,12+F12,18+F18,19+F19,3+F3,20+F20,22+F22,23+F23,21+F21,26+F26,27+F27,28+F28,33+F33,34+F34,30+F30,29+F29,31+F31,25+F25,5+F5,24+F24,32+F32,17+F17,14+F14,16+F16,15+F15,8+F8,2+F2,1=7 475 元. 图2 算法效果图 图3 修正效果图 对于求解最优H圈这样的NP难题,要使算法同时在精度、稳定性以及运行速度上达到最优几乎不可能.因此只能尽可能寻找平衡点,或根据不同的具体问题做出不同的选择.将算法与其他算法融合进行优化.比如,将换顶原理应用到二次逐次修正法中,可以提高修正速度,或者两者结合使用,可以得到更优解. 利用矩阵翻转法求得的最佳H圈与实际情形有所偏差,所以我们对模型进行改进,将理论可以直接相连而实际不能直接到达的城市之间的距离设为无穷大,为了方便处理,可以用999 999 km代表无穷大的数,这样对数据量化后,可以得到与实际接近的结果. 1)优点.模型在交通便利的情况下,也就是说在火车、飞机都可达的城市选择旅行路线是很准确方便的.这是一个推销员问题,因此不仅旅行路线的制定可以使用此模型,符合推销员思路的问题同样适用.另外我们使用的矩阵翻转法简单方便,易于掌握,可移植性也很强. 2)缺点.模型没有考虑一些偶然因素,比如当天的天气对交通的影响及对旅行消费的影响.由于这些原因,旅行的总费用要远远高于计算结果.所以我们只能假设旅行者不为经济原因而烦恼. [1] 龚劬.图论与网络最优化[M].重庆:重庆大学出版社,1998. [2] 杨秀文,陈振杰,李爱玲,等.利用矩阵翻转法求最佳H圈[J].后勤工程学院学报,2008,24(1):102-106. Matrix Inversion Method for Solving the Problem of Optimal Travel Route SHEN He-shuai, DUAN Bao-na (DepartmentofBasic,ZhengzhouVocationalCollegeofFinanceandTaxation,Zhengzhou450000,China) To obtain the best Hamilton ring (H ring), it realized the two successive corrections by matrix inversion method. This method is easy for programming,with the fast speed for calculation,especially fitting for the large number of vertex. the best route; matrix inversion method; two successive correction method 2014-11-27 申合帅(1981—),男,河南濮阳人,郑州财政金融职业学院基础部讲师. 10.3969/j.issn.1007-0834.2015.01.008 O224 1007-0834(2015)01-0025-03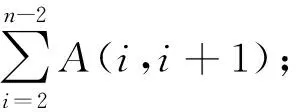
5 模型的进一步讨论
6 模型的优缺点
