钢筋混凝土圆形地下粮仓仓壁承载力计算方法研究

熊晓莉，金立兵，史笑珂，郭 辉

（河南工业大学 土木建筑学院，河南 郑州 450001）

0 引言

作为粮食生产和消费大国，我国具有悠久的储粮历史和丰富的储粮经验.在众多储粮仓型中，地下仓因其具有节能、节地、隐蔽、防火、防爆、污染少等特点，应用于大型储粮体系具有明显优势.作为一种绿色生态储粮方式，钢筋混凝土地下粮仓无论结构形式还是承载特性与现有的喇叭形地下粮仓有着很大差异，了解其承载力性状具有重要意义.

我国作为储粮大国，在新型仓储结构形式的研究与开发方面一直处于世界前列.20 世纪末，我国专家对多种仓型进行试验研究和讨论后确定喇叭形地下仓是一种结构稳定、设计合理、能够充分利用土体自稳能力的先进仓型，一般是地下水位较低的黄土和黏性土地区优越的储粮仓型，并被确定为地下粮仓的主要仓型，在国家各粮食储备库中进行了推广应用[1].鉴于喇叭形地下仓仓容较小，2001 年国家粮食储备局郑州科学研究设计院设计了一种浅埋大型房式仓，该仓设计的容量50 000 t，单仓存量8 600 t，装粮高度7 m，将仓内地坪下挖2.3 m 增加单仓容量，具有占地面积小、能充分利用地下空间增加储粮的特点[2].2008—2009 年，王录民等[3-5]提出了一种新型的“圆筒围成的大空间地下粮仓”结构形式，并采用非线性有限元法对大型地下筒围仓在周围土体静态作用下的外壁应力和变形进行了分析，指出应在受拉区配置一定数量的钢筋，在利用有限元法分析仓土共同作用时，计算模型应尽可能简化.郑培等[6]提出了“地下矩形筒围仓”结构形式，在考虑了整个结构空间相互作用的前提下，利用有限元软件对地下矩形筒围仓进行分析，指出仓顶板存在挠度过大的问题和边柱顶端存在应力突增问题，需进一步研究解决.涂成顺[7]利用初参数法和有限元法对地下大直径钢筋混凝土筒仓仓壁的简化计算模型进行了内力和位移分析，未考虑地下筒仓底板厚度取值对仓壁约束方式的影响.付明堂[8]利用有限元法计算了矩形地下仓在简化的土压力作用下的变形，分析结构的位移场和应力场分布规律.此外，国外已建成的地下仓大多以周围岩石作为外层防护[9-11]，地下仓的建设受地理因素影响较大，仓容较小，没有充分利用地下空间，不利于推广应用.

综上，国内外的大部分研究工作主要集中于地下粮仓整体结构形式的改进及岩体地下仓的推广应用方面，对钢筋混凝土地下粮仓仓壁承载机理研究较少；在分析过程中均未涉及地下水压力的影响；在进行少量的仓体承载性能的理论研究过程中基本上采用有限元法，分析结果未得到其他理论分析方法的验证.作者选取水土压力作用下的空仓状态作为最不利受力条件，分别采用下端固定、上端简支圆柱壳模型分析法和有限元整体分析法计算仓容100 t 的地下试验仓仓壁竖向弯矩和环向力，分析了仓壁竖向弯矩和环向力分布规律，研究了钢筋混凝土地下粮仓仓壁承载特性.

1 工程概况

为研究钢筋混凝土地下粮仓承载特性，在位于郑州市中牟县郑庵镇前路俭和后路俭村、万三公路东面、陇海铁路以南的河南金地集团粮食物流园区内制作了仓容100 t 的地下试验仓.该地下圆形粮仓外径2.5 m；仓壁竖直段高度8 m；仓顶为梁板结构，仓壁为圆柱筒形，仓底为圆台锥底；仓顶板厚250 mm，仓壁壁厚250 mm，仓底板厚500 mm；仓顶埋深-2.250 m，仓底埋深-10.250 m，设计地下水位为-1.000 m；自然填土为砂土（天然重度为16 kN/m3，φ=35°；地下水位以下，饱和重度为20 kN/m3，φ=25°）；仓壁混凝土强度等级C35；仓壁钢筋采用HRB400 级.地下试验仓结构参数如图1 所示.

图1 地下试验仓结构参数示意图Fig.1 Structure parimeter of test granary

2 承载力计算

2.1 工程实用计算方法

本工程计算模型的选取可参考《给水排水工程结构设计手册》[12]进行.仓壁计算高度H=8 m，计算半径R=2.250+0.250/2=2.375 m，仓壁厚h=0.25 m，圆柱壳弹性特征系数m.因1＜H/s=13.652＜15，仓壁可按下端固定、上端简支的圆柱壳计算环向力及竖向弯矩，计算简图如图2 所示.

图2 仓壁计算简图Fig.2 Calculation diagram of granary wall

根据分析可知，仓内无贮料，仓外有土及水压力时，结构受力最不利.此时，地下仓结构按照承载力极限状态设计的荷载效应基本组合设计值计算参数，取值见表1.

表1 中的荷载标准值计算过程为：地下水位以上部分，仓壁侧向土压力标准值，按天然重度计算主动土压力；地下水位以下按有效重度计算主动土压力.仓壁计算截面处单位面积上的侧向土压力标准值ps（kPa）：

式中：ks为主动土压力系数，地下水位以上取tan2（45°-35°/2）=0.271，地下水位以下取tan2（45°-25°/2）=0.406；γs为填土的重度，kN/m3，地下水位以上取天然重度16 kN/m3，地下水位以下取有效重度10 kN/m3；z 为室外±0.000 至计算截面的距离，m.

进出粮期间的车辆荷载，可偏于安全的选用50 t 的重型卡车（车身长度方向最大轴距lt为7.8 m，车身宽度方向的最大轮距ht为1.8 m），仓顶覆盖土层厚度zt为2.25 m，可按照换算成等效均布土层厚度的方法[13]来计算.车辆荷载的等效均布土层厚度he（m）计算：

表1 仓壁水平荷载标准值、分项系数、组合系数及设计值Table 1 Standard value,partial factor，combined factor and design value of horizontal loads on granary wall

式中：Gt为车辆总重力，kN；Lt为计算宽度，m，Lt=lt+2zt·tan30°=10.4 m；Ht为计算长度，m，Ht=ht+2zt·tan30°=4.4 m.

作用于仓壁计算截面处单位面积上的水压力pw（kPa）按下式计算：

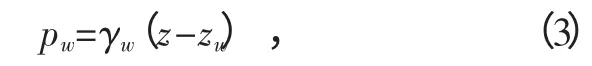
式中：γw为水的重度，取9.8 kN/m3；zw为地下水位线至室外±0.000 的距离，m；若计算得pw＜0 取pw=0.

根据表1 中的计算数据，可得仓壁水平荷载设计值如图3 所示.

由计算模型及荷载计算结果，结合文献[12]静力计算查表获得仓壁的弯矩和轴力.在计算时将梯形分布的仓壁水平荷载分为三角形部分和矩形部分分别查文献[12]计算.约定仓壁弯矩外侧受拉为正，轴力受拉为正.查表系数H2/（2Rh）=82/（2×2.375×0.25）=54.

图3 仓壁水平荷载设计值Fig.3 Design value of horizontal load on granary wall

荷载基本组合条件下仓壁所受竖向弯矩（（kN·m）/m）和环向力（kN/m）见表2.

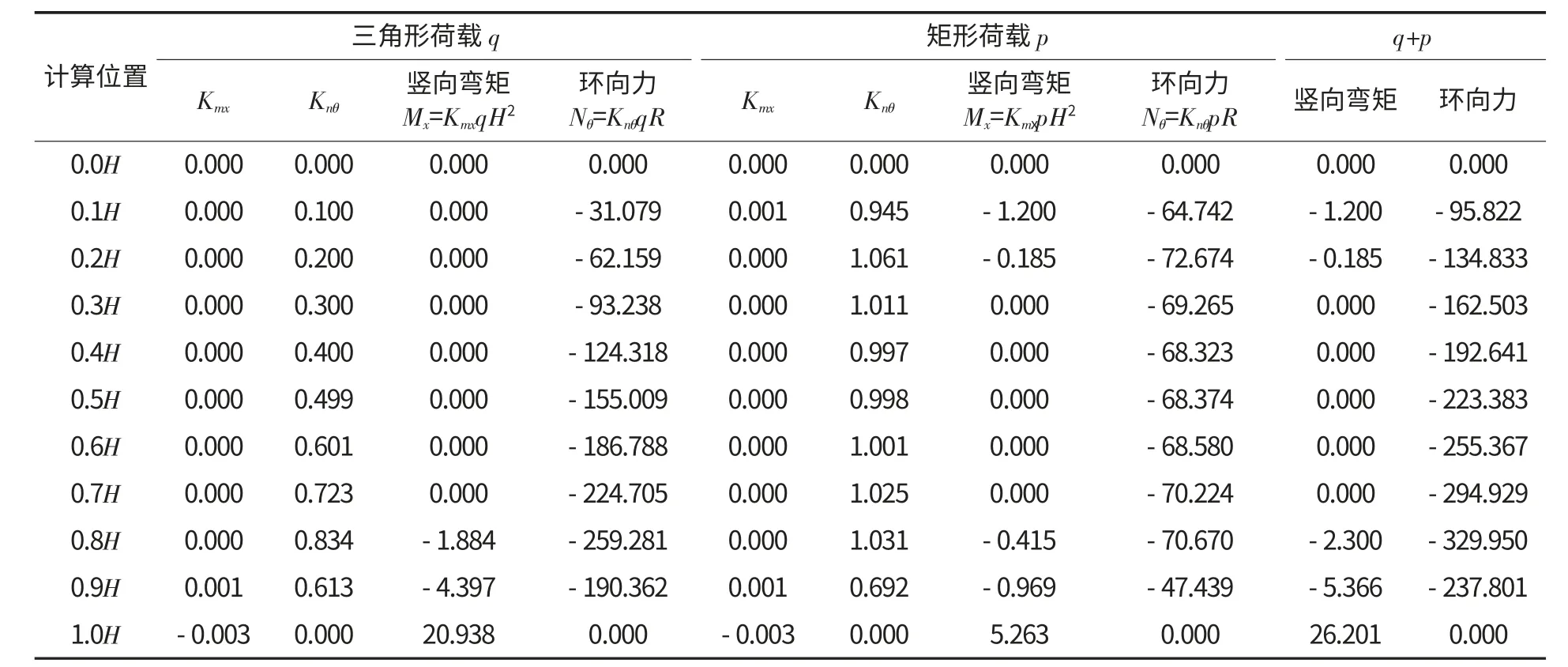
表2 基本组合条件下仓壁竖向弯矩和环向力Table 2 Radial moment and circumference force of wall under fundamental combination

2.2 FEA 方法

利用有限元软件ANSYS 对地下仓整体进行受力分析研究时，选取壳单元Shell63 来模拟仓顶、仓壁及仓底.钢筋混凝土弹性模量E 取30 000 MPa，泊松比v 取0.2.因简化分析过程需要，在重点研究仓壁受力时，暂不考虑仓顶主次梁和环梁的建模，也不考虑仓顶进粮口的位置和大小.

仓顶施加竖向压力（包括仓顶自重、土压力、仓顶活载、设备操作荷载、安装检修荷载、车辆荷载、水压力）基本组合值77.86 kN/m2，方向由仓外指向仓内；仓底施加竖向压力（包括仓底自重和仓底水压力）基本组合值78.92 kN/m2，方向由仓外指向仓内；仓壁施加图3 中线性分布的水平压力基本组合值，方向由仓外指向仓内.

模型约束的施加需要考虑地下水位变化引起的支座位置改变.当地下水位较低时，地下水浮力小于仓体自重，仓体支座位于仓底部位，应在整体结构模型的仓底节点上施加z 向约束；当地下水位较高时，地下水浮力大于仓体自重，仓体支座位于仓顶部位，应在整体结构模型的仓顶节点上施加z向约束.取上述两种约束形式下仓壁的最不利受力状态作为其承载能力极限.

对有限元模型进行进行静力求解并显示仓壁应力云图.仓底支承时的仓壁应力云图如图4 所示；仓顶支承时的仓壁应力云图如图5 所示.

图4 仓底支承的地下仓仓壁应力云图Fig.4 Stress nephogram of wall of underground granary with bottom support

图5 仓顶支承的地下仓仓壁应力云图Fig.5 Stress nephogram of wall of underground granary with top support

2.3 计算结果

将ANSYS 分析所得仓壁z 向（高度方向）应力按照式（4）转化为仓壁竖向弯矩，并将其沿仓壁高度绘制成曲线，如图6 所示.

图6 仓壁竖向弯矩对比Fig.6 Comparison of radial moment of granary wall

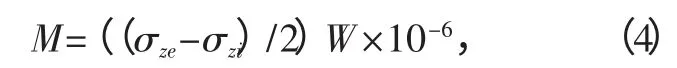
式中：M 为仓壁单位长度的竖向弯矩，（kN·m）/m；σze为仓壁外侧z 向应力，N/mm2，受拉为正；σzi为仓壁内侧z 向应力，N/mm2，受拉为正；W 为仓壁单位长度的抗弯模量，mm3.

将ANSYS 分析所得仓壁环向应力按照式（5）转化为仓壁环向力，并将其沿仓壁高度绘制成曲线，如图7 所示.

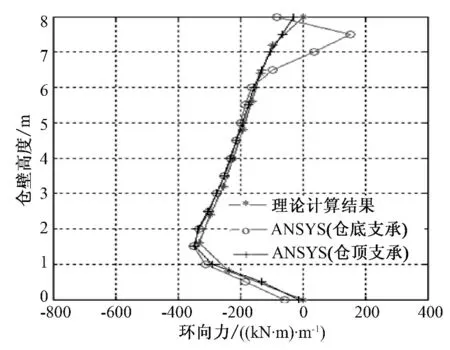
图7 仓壁环向力对比Fig.7 Comparison of circumference force of granary wall

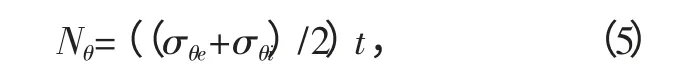
式中：Nθ为仓壁单位长度的环向力，kN/m；σθe为仓壁外侧应力，N/mm2，受拉为正；σθi为仓壁内侧应力，N/mm2，受拉为正；t 为仓壁厚度，mm.

对比图6 和图7，结果表明：

（1）仓壁中段竖向弯矩及环向力两种计算方法所得结果相差不大，仅在仓壁上、下边缘处（即仓壁与仓顶连接处、仓壁与仓底连接处），因边缘约束效应的影响，有较大差异.

（2）地下仓结构的实际约束为仓顶与仓壁弹性连接（后者刚度大于前者），仓底与仓壁弹性连接（前者刚度大于后者），而工程实用计算方法是以下端固定、上端简支的圆柱壳为对象分析，下端约束较实际强，上端约束较实际弱.

（3）FEA 方法中，仓底支承的ANSYS 模型约束了仓底各节点的z 向位移，约束较实际强，较理论计算的完全固定弱，上端约束与实际相符，即仓顶与仓壁弹性连接.

（4）FEA 方法中，仓顶支承的ANSYS 模型约束了仓顶各节点的z 向位移，约束较实际强，较理论计算的简支也强；下端约束与实际相符，即仓底与仓壁弹性连接.

（5）FEA 方法采用整体建模计算的处理方式，可以得到更为精确的分析结果.在利用此方法进行地下仓承载力分析时，仓壁受力沿高度H 自上而下：0～0.2H 范围内宜取仓底支承时的结果，0.2H～0.8H 范围内宜取仓顶（仓底）支承时的结果，0.8H～H 范围内宜取仓顶支承时的结果.

3 结论

工程实用计算方法无法准确考察壳体边缘约束效应的影响，FEA 方法能更精确地展示地下仓整体结构的受力情况.

建议采用FEA 方法对钢筋混凝土地下仓结构进行承载力分析，仓壁结构沿高度H 自上而下：0～0.2H 范围内宜按仓底支承时的计算结果设计，0.2～0.8H 范围内宜按仓顶（仓底）支承时的计算结果设计，0.8～1H 范围内宜按仓顶支承时的计算结果设计.

仓壁与仓顶连接处、仓壁与仓底连接处应力状态比较复杂，为避免连接处承载力不足发生破坏，可将仓顶和仓底结构做成梁板结构或是曲面结构以减小该处弯矩所产生的拉应力，并在仓壁上、下边缘处设置水平方向环梁以抵抗该处水平方向的张力.

［1］王子林，张龙川.建设新型土体地下仓实现储粮安全保鲜［J］.粮食储藏，2000，29（3）：22-26.

［2］白玉兴，司永芝，徐晓娟.大型房式仓的设计与应用研究［J］.粮食流通技术，2006（1）：18-20.

［3］余汉华，王录民，王振清，等.我国地下粮仓应用的现状及前瞻［J］.河南工业大学学报：自然科学版，2008，29（6）：79-81.

［4］余汉华.新型地下仓储结构有限元分析［D］.郑州:河南工业大学，2009.

［5］王录民，余汉华，王振清，等.地下圆筒围仓在土体作用下的接触分析［J］.河南工业大学学报：自然科学版，2009，30（3）：1-3，16.

［6］郑培，刘银来，王振清.我国地下粮仓新仓型初探及其有限元分析［J］.河南工业大学学报：自然科学版，2009，30（3）：91-94.

［7］涂成顺.地下大直径钢筋混凝土筒仓仓壁结构分析及比较［D］.郑州：河南工业大学，2011.

［8］付明堂.地下仓结构变形与应力分析［D］.郑州：河南工业大学，2011.

［9］陈彦岭，罗济章.芬兰的地下仓储设施［J］.地下空间，1990，10（3）:236-241.

［10］Gentile R J.Geology and utilization of underground space in metropolitan Kansas City area，USA［J］.Environmental Geology，1997，29（1-2）：11-16.

［11］Zevgolis I E，Mavrikos A A，Kaliampakos D C.Construction，storage capacity and economics of an underground warehousing logistics center in Athens，Greece［J］.Tunnelling and Underground Space Technology，2004，19（2）:165-173.

［12］《给水排水工程结构设计手册》编委会.给水排水工程结构设计手册［M］.2 版.北京：中国建筑工业出版社，2007.

［13］JTGD 60—2004，公路桥涵设计通用规范［S］.