一种基于MUSIC 算法的涡街信号处理方法

张琼丹，蒙建波

(重庆大学 自动化学院，重庆400030)

0 引 言

涡街流量计以其介质适应性强、压力损耗小、量程范围大等诸多优点，在流量测量中得到广泛应用。实际应用中，由于管道的振动和流场的不稳定，涡街信号极易被淹没在噪声中。目前，涡街信号的处理方法主要有:基于FFT 的周期图法［1］、基于Burg 的现代谱估计法［2］、自适应陷波方法［3］、Rife 法［4］等，这些方法均有各自优势。迄今为止，尚未发现多重信号分类(multiple signal classification，MUSIC)算法［5～7］应用于涡街信号的处理。MUSIC 算法是基于自相关矩阵特征分解，利用信号子空间和噪声子空间的正交性对信号进行高分辨估计的一种方法，适合于普遍情况下的正弦信号参数估计。由于涡街信号的理想波形为正弦波，因此，本文将MUSIC 算法应用于涡街信号的处理，以获得高精度的涡街信号频率点。

1 涡街流量计信噪特性

1.1 涡街流量计测量原理

在流体中放置一定形状的漩涡发生体，则漩涡发生体两侧会交替产生规则的漩涡，在一定的雷诺数范围内，产生的漩涡是稳定的。涡街流量计的稳定漩涡脱落频率f 与流速v 有如下关系

其中，Sr 为斯特劳哈尔数，d 为漩涡发声体特征尺寸，D为管道直径。当雷诺数Re 在3×104～3×106范围内，流速v 与漩涡脱落频率f 的关系确定，因此，仅需检测频率f即可获得流体的流量。

1.2 涡街信号模型

涡街流量计的信号由压电晶体传感器产生，在理想情况下，由于流体的流场是稳定的，因此，检测到的涡街信号是一正弦信号。但在实际工业现场中，涡街信号可能混杂高斯白噪声、周期性脉冲噪声、谐波噪声等各类噪声，因此，建立如下的离散随机信号模型

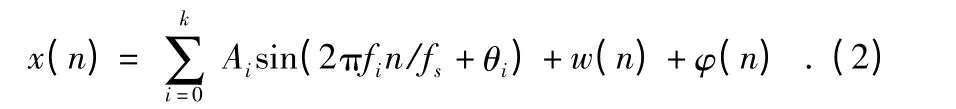
其中，n=0，1，…，N－1，k 为基波、谐波总数，且k≤3;Ai，fi，φi分别为基波和谐波的幅值、频率、相位;fs为采样频率;w(n)和φ(n)分别为高斯白噪声和脉冲噪声。

2 MUSIC 算法

MUSIC 算法是一种以自相关矩阵特征值分析为基础的非参数设计方法。假设系统由复正弦信号和噪声构成，并且自相关矩阵R 包含两个子空间信息:信号子空间和噪声子空间。因此，矩阵特征向量亦可分为信号子空间和噪声子空间。为求得功率谱估计，可采用自相关矩阵特征值分析法计算出信号子空间和噪声子空间的特征值向量函数，使其函数值在正弦信号频率处函数值最大。

设序列x(n)是由M 个复正弦加噪声构成，自相关函数Rx(k)为

若有(p+1)个Rx(k)组成相关阵

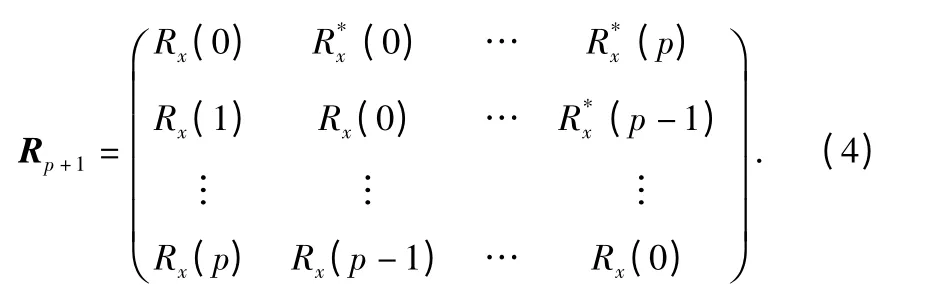
定义信号变量ei

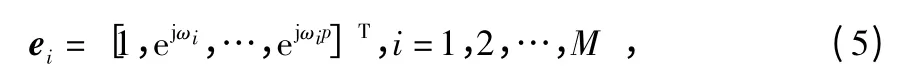
则有

将式(6)作特征分解可得

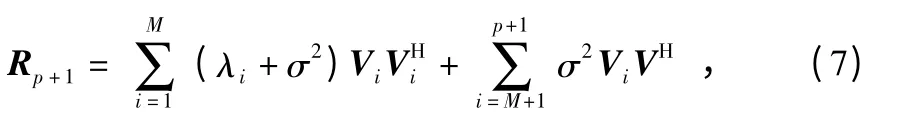
式中 Vi为主特征向量，且相互正交。可知V1，…，VM构成信号子空间，其特征值为λi+σ2;VM+1，…，Vp+1构成噪声子空间，其特征值为σ2。定义MUSIC 法谱估计的函数为

信号角频率ω 的估计可由函数Pmusic(ω)的M 个峰值位置确定。谱函数Pmusic(ω)的波峰位置反映了信号的频率值，但其并非信号的功率谱，一般称其为MUSIC 谱。

为提高低信噪比下谱估计的准确度，引入加权系数λk，通过对噪声子空间的特征向量加权，使得不同特征向量对MUSIC 谱的作用不同。加权所得谱估计为

3 仿真研究

为验证MUSIC 算法分辨涡街信号频率的有效性，分别针对工程中典型的高斯白噪声、周期性脉冲噪声和谐波噪声进行仿真研究。

3.1 高斯白噪声背景下的仿真

高斯白噪声是一种概率密度函数满足高斯分布、功率谱密度均匀分布的噪声。设高斯白噪声序列为w(n)，其满足(0，σ2)的高斯分布，原始正弦信号序列为s(n)，则涡街信号x1(n)可表示为

利用Matlab 软件产生如上的涡街信号x1(n)，其中，原始正弦信号频率fo=200 Hz，信噪比SNR=10 dB，采样频率fs=3 072 Hz，其仿真结果如图1 所示。

图1(a)为高斯白噪声下的涡街信号波形，其信号幅值显著变化。图1(b)为分别采用周期图法和MUSIC 法获得的功率频谱，对比可知，采用周期图法的频谱分辨率较低，信噪比较低;采用MUSIC 法得到的频谱曲线平滑，频率分辨得到明显改善，信噪比得到显著提高。

图1 高斯白噪声下的仿真结果Fig 1 Simulation results under Gaussian white noise

3.2 周期性脉冲噪声背景下的仿真

α 稳定分布模型是一种较好描述脉冲噪声的数学模型，其特征函数为

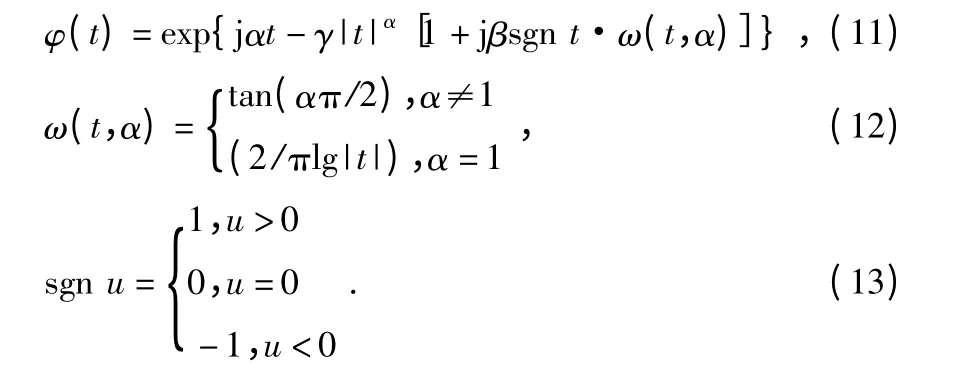
其中，α 为特征指数，用来度量分布拖尾的厚度;β 为对称参数，β=0 表示对称α 稳定分布;γ 为分散系数，衡量分布的宽度;μ 为位置参数。α 越小，拖尾越重。

利用Matlab 软件产生一个由正弦信号s(n)和脉冲信号φ(n)组成的涡街信号x2(n)，其中，正弦信号s(n)频率fo=200 Hz，脉冲信号φ(n)服从α 稳定分布，α=2，β=γ=0，脉冲信号的频率fφ=50 Hz，采样频率fs=3 072 Hz，其仿真结果如图2 所示。

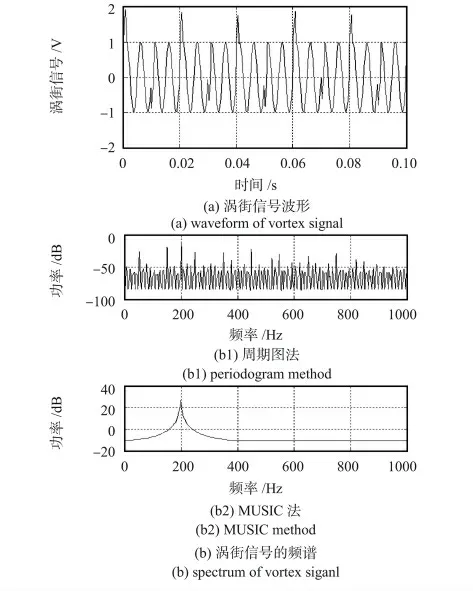
图2 周期性脉冲噪声下的仿真结果Fig 2 Simulation results under periodic pulse noise

图2 (a)为周期性脉冲噪声下的涡街信号波形，其信号幅值存在周期性尖峰。图2(b)为分别采用周期图法和MUSIC 法获得的功率频谱，对比可知，采用周期图法的频谱分辨较差，其存在多个幅值较大的谱峰;而采用MUSIC法得到的频谱，正弦信号的谱峰分辨效果依旧良好。

3.3 谐波噪声背景下的仿真

实际应用中常存在一定的谐波噪声，为验证MUSIC 算法的有效性，在上述噪声环境中进行仿真研究。受干扰的涡街信号x3(n)可表示为

其中，正弦信号频率fo=200 Hz，谐波频率f1，f2分别为400，600 Hz，采样频率fs=3 072 Hz，其仿真结果如图3 所示。

图3(a)为周期性脉冲信号下的涡街信号波形，图3(b)为分别采用周期图法和MUSIC 法获得的功率频谱。可知两者均对频率点分辨准确，但周期图法对谐波分量的幅值分辨较差。

上述结果表明:相对于传统的周期图法，MUSIC 算法在复杂噪声环境中表现出更优的性能，其对提高涡街流量计的抗干扰能力具有重要意义。

图3 谐波噪声下的仿真结果Fig 3 Simulation results under harmonic noise

4 结 论

针对复杂噪声环境下的涡街信号处理，本文引入了基于MUSIC 算法的谱估计，建立了涡街信号模型，阐述了MUSIC 算法的基本原理，在此基础上进行了仿真验证。仿真结果表明:MUSIC 算法可以有效地滤除典型的高斯白噪声、周期性脉冲噪声及谐波噪声，保证了获取涡街信号频率的高精度，是一种新型的涡街信号处理方法。

［1］ 江文斌，秦会斌，邵李焕，等.基于经典谱估计改进方法的涡街流量计［J］.仪器仪表学报，2012，33(1):229－234.

［2］ 孙志强，陈延平.基于Burg 法AR 模型谱估计的涡街流量计旋涡脱落频率提取［J］.中南大学学报:自然科学版，2013，44(4):1684－1688.

［3］ 徐科军，汪安民.涡街流量计信号估计的自适应陷波方法［J］.仪器仪表学报，2000，21(2):206－207，214.

［4］ 孙宏军，徐冠群.基于相角判据的Rife 算法的涡街信号处理方法［J］.仪器仪表学报，2013，34(12):2860－2866.

［5］ 刘景森，金 勇.一种基于吉布斯抽样的MUSIC 多维参数联合估计算法［J］.传感器与微系统，2008，27(6):62－65.

［6］ 孙永梅，赵 维，阚园园.脉冲噪声环境下的改进MUSIC 谱估计方法［J］.大连交通大学学报，2012，33(3):67－72.

［7］ 何子述.现代数字信号处理及其应用［M］.北京:清华大学出版社，2009:110－116.