基于介数中心性的无线传感器网络抗毁性评价方法*
2015-03-27罗小娟
王 灿,吴 雪,罗小娟
(华东理工大学 信息科学与工程学院,上海200237)
0 引 言
抗毁性是衡量无线传感器网络(wireless sensor networks,WSNs)在部分节点发生内部故障或者受到外界有意攻击而失效时,网络仍能维持其正常功效的能力[1]。目前国内外针对网络抗毁性测度的研究很多,大部分的方法都是以网络连通性来进行衡量。文献[2]首先从网络连通度角度考虑提出了WSNs 的两个抗毁性测度:有效连通子图和最大连通子图。文献[3]提出了基于节点重要度的WSNs 抗毁熵测度模型。文献[4]提出了基于节点介数的网络结构熵,该方法可以有效地评估一般复杂网络的抗毁性特征。
WSNs 不同于一般复杂网络之处在于它以数据收集为中心,本文针对这一特性,提出了WSNs 节点介数中心性概念,用以评估网络中节点的重要性。基于文献[5]提出的网络结构熵,本文提出了介数熵抗毁性测度模型,仿真结果表明:它能全面、准确地评估WSNs 抗毁性。
1 WSNs 节点介数中心性
节点之间数据的传输主要依赖于最短路径,如果某个节点被许多最短路径经过,则说明该节点在网络中很重要。介数中心性定义为网络中所有最短路径中经过某一节点的路径数目在最短路径总数中占有的比例,反映了相应的节点在整个网络中的作用和影响力[6]。因此,可利用介数中心性来度量节点重要性。
相比于一般复杂网络,WSNs 是以数据收集为目的,每个节点都要将收集到的数据传递给汇聚节点。因此,还需要考虑汇聚节点的因素。
如图1 所示,当汇聚节点在WSNs 的右侧时,信息会由左向右传递,如箭头所示,此时节点4 和5 将是网络核心节点,其重要性最高。当汇聚节点位于WSNs 的上方时,信息将沿着由下往上方向传递,此时网络核心节点将是节点1和6。
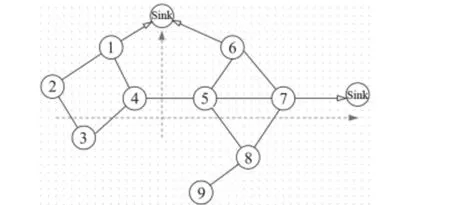
图1 汇聚节点位置对节点中心性的影响Fig 1 Effect of location of sink node on node centrality
本文基于复杂网络的介数中心性[7],并结合WSNs以数据收集为中心这一特点,提出WSNs 介数中心性定义为

其中,n 为网络节点数,nk(i)为节点k 到汇聚节点的最短路径中经过节点i 的个数,nk为节点k 到汇聚节点的所有最短路径的个数,节点k 为网络中除汇聚节点外的任意节点。
由图2 所示为WSNs 拓扑结构,分别利用复杂网络节点介数中心性度量方法和本文提出的WSNs 节点介数中心性来计算每个节点的中心性,结果如表1 所示。

图2 一种典型的WSNs 拓扑结构Fig 2 A typical topology structure of WSNs
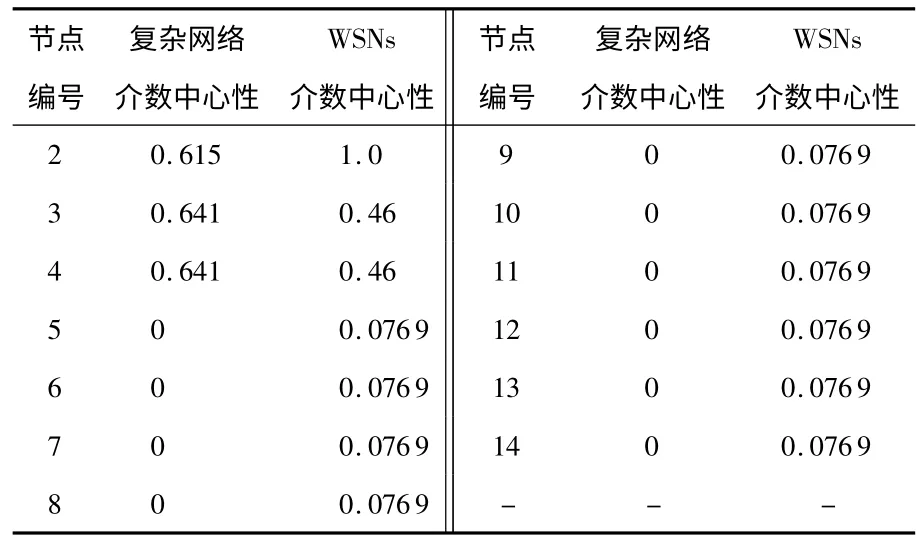
表1 两种中心性度量对比Tab 1 Comparison of two centrality measurement
分析表1 可以看到:利用复杂网络节点介数中心性,节点3 和节点4 都比节点2 的数值大,但是在实际网络中,一旦节点2 失效,整个网络就会崩溃,而节点3 或者节点4 失效后,网络50%的节点依旧可以正常工作,因此,在实际网络中节点2 比节点3 和节点4 都重要。对比分析本文提出的WSNs 介数中心性,节点2 的WSNs 介数中心性值是节点3 和节点4 数值的2 倍,而其他节点的介数中心性值都要比上述三个节点小,这与实际网络结构是相符的。由此可见,本文提出的WSNs 介数中心性可以更准确地定量描述一个节点的重要性。
2 WSNs 介数熵测度模型
由于网络拓扑结构中含有核心节点,这些节点往往处于比较重要的位置,这就意味着利用该节点进行信息传递的次数可能会远远超过其他节点。另外,这些节点承受的信息负载量重。转发信息时更容易出现数据包丢失,拥塞加剧,最终导致链路中断等情况。因此,可从节点重要性考虑,建立抗毁性测度模型。由前述可知,本文提出的WSNs节点介数中心性可以有效地评估网络中节点的重要性,在此基础上,给出节点的抗毁度概念,节点抗毁度表示为


3 网络抗毁性仿真分析
在Matlab 2014 环境下进行模拟仿真研究,有WSNs 的网络拓扑如图3 所示,分别对其采用基于度数的网络结构熵方法、文献[4]中基于节点介数的网络结构熵方法、本文提出的介数熵方法进行抗毁性测度分析,仿真结果见表2。
3.1 介数中心性最高节点失效后抗毁性分析
为整个网络所有节点的WSNs 介数中心性之和,提出的节点抗毁度用来衡量节点对网络抗毁性的贡献。如果网络是均匀的,各个节点的抗毁度相差不大,则认为该网络是均匀的;反之,如果网络中有少量的关键节点,其抗毁度较大,另外还有很多的边缘节点,节点的抗毁度较小,则可以认为这种网络是不均匀的。为度量WSNs 节点抗毁度的均匀性,本文提出了介数熵测度模型,WSNs 介数熵为

其中,Si为节点i 的抗毁度。介数熵反映的是节点抗毁度分布的差异性,网络节点抗毁度差异性越小,熵值就越大,面对选择性攻击的抗毁性能越好;反之,则面对选择性攻击的抗毁性能越差。
基于介数熵的WSNs 抗毁性评价方法的算法步骤:
1)计算各节点至汇聚节点的最短路径。
3)根据公式(2)计算每个节点的WSNs 抗毁度Si。
4)根据公式(3)计算该网络的介数熵E,给出网络的抗毁性测度。
在图3 所示的网络拓扑图中,选择攻击介数中心性最高的节点6,节点6 失效后,网络拓扑图如图4 所示。分析表2 中数据可以看出:基于节点度的网络结构熵评估出的网络抗毁能力,在节点6 失效后,基本没有发生变化(变化率约为0.08%);而文献[4]中提出的基于节点介数网络结构熵,得出的结果显示,网络抗毁性下降了52.4%;根据本文提出的介数熵模型计算结果为0,表示网络中不存在通往汇聚节点的最短路径。从节点6 失效的实际意义来看,节点6 是连接节点5、节点7、节点12 三个节点所控制的各自小网络的枢纽,节点6 失效后,这三个小网络就只能在各自内部通信,失去了和汇聚节点通信的能力,对于WSNs 而言,网络已经崩溃。因此,前两种方法在评估节点6 这样的度数虽然不大,但是介数很大的节点受到攻击后,对WSNs连通性造成的影响方面存在着极大的不足,而本文提出的介数熵,则可以有效地评估网络抗毁能力。

图3 初始网络拓扑图Fig 3 Initial network topology

图4 节点6 失效后的网络拓扑图Fig 4 Network topology after node 6 is failed
3.2 节点度最高节点失效后抗毁性分析
在图3 中,节点度最高的点是节点5、节点7 和节点12,且三个节点的失效对网络影响是等效的,不失一般性,选择攻击节点5,图5 为节点5 失效后的网络拓扑。再次分析表2 中的数据,基于节点度的网络结构熵和文献[4]中的基于节点介数网络结构熵熵值都有所下降,下降的比值分别为14.7%和19.9%,本文提出的介数熵则下降了33.3%。结合实际网络分析,节点5 失效后,节点5 所控制的那部分小网络失去了跟汇聚节点通信的能力,即节点5的失效直接导致了网络中有1/3 的节点随之失效,网络整体连通性下降了1/3,由此可见,本文提出的介数熵更准确地反映了这种破坏程度下网络的抗毁性测度。
3.3 叶节点失效后网络抗毁性测度分析

图5 节点5 失效后的网络拓扑图Fig 5 Network topology after node 5 is failed
在图3 所示的网络拓扑图中,除节点5、节点6、节点7和节点12 外,剩余节点都是叶节点,且这12 个叶节点的失效对网络影响是等效的,不失一般性,选择攻击节点1,节点1 失效后的网络拓扑如图6 所示。分析表2 中的数据,基于节点度的网络结构熵和文献[4]中的基于节点介数网络结构熵的熵值都有所下降,下降的比值分别为12.23%和12.22%,本文提出的介数熵则下降了6.25%。结合实际网络分析,节点1 失效后,仅节点1 失去了跟汇聚节点通信的能力,网络失去了16 条通信链路中的一条,对比之下,本文提出的介数熵更好地反映了WSNs 在这种破坏情况下的抗毁性程度。

图6 节点1 失效后的网络拓扑Fig 6 Network topology after node 1 is failed

表2 基于不同网络熵的抗毁性测度对比Tab 2 Invulnerability measurement comparison based on different WSNs entropy
综上,可以得出结论:本文提出的介数熵在评估WSNs抗毁性能时,具有更好的效果,并且利用该测度模型来评估网络抗毁性能的好坏时考虑了选择性打击的方式,因而,该方法更全面地评估了网络的抗毁性。
4 结 论
网络抗毁性在一定程度上反映了网络能够抵御攻击的能力。现实中的网络呈现出节点度分布符合幂率分布的无标度特性,即大量的节点拥有较小的连接,而少数节点却存在较大的连接。网络的这种不均匀特性,可以用物理意义上的“熵”来表征。由此,本文提出了介数熵的网络抗毁性测度模型,仿真分析表明:使用该测度模型能够有效、客观地反映网络在受到不同程度攻击后网络抗毁性的变化情况。
[1] 郑耿忠,刘三阳,齐小刚.基于无标度网络的无线传感器网络拓扑演化模型研究[J].高技术通讯,2011,21(11):1219-1225.
[2] Fu Xiuwen,Li Wenfeng.Empowering the invulnerability of wireless sensor networks through super wires and super nodes[C]∥13th IEEE/ACM International Symposium on Cluster,Cloud,and Grid Computing,2013:561-568.
[3] 邹训丽.基于复杂网络理论的无线传感器网络抗毁性测度研究[D].上海:华东理工大学,2012:21-33.
[4] 刘媛妮.复杂网络抗毁性建模优化及其评估技术研究[D].北京:北京邮电大学,2011:97-112.
[5] 吴 俊,谭跃进.网络结构熵及其在非标度网络中的应用[J].系统工程理论与实践,2004(6):1-3.
[6] 荣莉莉,郭天柱,王建伟.复杂网络中心性[J].上海理工大学学报,2008,30(3):227-236.
[7] Freeman C.A set of measures of centrality based upon betweenness[J].Sociometry,1977,40(1):35-41.
