压应力条件下不同晶界对石墨烯弯曲变形的影响

喻 娟，张效迅，吉建莎，黄 丹，习 武

(上海工程技术大学 材料工程学院，上海 201620)

石墨烯是由 sp2杂化的碳原子构成的单层蜂窝状二维薄膜材料，近年来，石墨烯因为其特殊性能引起了很大的关注[1-2]。在金属基上可以制备大面积的石墨烯，但制备的石墨烯不可避免地含有较多晶界缺陷[3-4]。DOU 等[5]采用电泳沉积耦合电化学还原法制备石墨烯薄膜，LENG等[6]采用微波辐照法制备少层石墨烯。王永祯等[7]研究发现，在(1000±50) ℃的温度范围内，采用化学气相沉淀法可以制备高质量的少层石墨烯；但是，采用该方法制备的石墨烯含有缺陷，这些缺陷会严重影响石墨烯的性能[8-9]。韩同伟等[10]通过分子动力学模拟证明缺陷会使石墨烯拉伸强度下降7%左右。在这些缺陷中，晶界是最常见的一种[11]。目前，采用扫描透射电子显微镜实验可以清楚地观察到在铜基上通过化学气相沉淀法制备的石墨烯晶界[12]；通过第一性原理和原子模拟，可以观察到这些晶界是由周期性的连续的五元环和七元环对组成的[13-14]。YAZYEV等[15]和LIU等[16]运用基本拓扑缺陷方法在石墨烯中建立不同的位错和晶界模型。NEEK-AMAL等[17-18]通过对石墨烯施加轴对称压应力，研究杂乱分布的缺陷对石墨烯热机械性能的影响。NEEK-AMAL等[19]研究了两个不同晶界对无自由边界石墨烯纳米带弯曲性能的影响，表明大角度晶界石墨烯带的弯曲比小角度的大，并且固定石墨烯带的边界会使其不稳定。FRANK等[20]研究在压应力下基底上单层石墨烯的起皱行为，提出完美石墨烯约能被压缩6%。GALASHEV等[21]研究之字形边界上能承受压力比扶手椅形边界的大。压应力条件下，完美石墨烯力学性能的研究和晶界对石墨烯机械稳定性能影响的研究都很多，但压应力条件下晶界对石墨烯弯曲变形机理影响的研究尚未见报道，了解晶界对石墨烯性能的影响对制备下一代石墨烯产品有着至关重要的作用。本文作者研究了在压应力条件下，晶界角为21.8°、32.2°、38.2°和 60°的晶界对石墨烯弯曲性和稳定性的影响。

1 模拟方法

通过分子动力学模拟可以得到石墨烯晶界模型[22-23]，用LAMMPS软件执行对石墨烯的轴对称压缩模拟。研究者们通常采用 Morse势函数、REBO(Reactive empirical bond order)势函数和 AIREBO(Adaptive intermolecular reactive empirical bond order)势函数来模拟石墨烯[16]。Morse势函数是一个两体反应势函数，不包括多体之间的相互作用；由于REBO势场没有键与键之间的相互作用，因此它不适合石墨烯这种含有大量原子相互作用的系统[24]。而AIREBO是REBO的延伸，AIREBO包含REBO不包括的四体之间的扭转作用[25]，AIREBO势场包含了非成键之间的作用；在石墨烯压缩弯曲模拟中，相互扭转有着相当重要的作用。AIREBO势场适用于截断半径为1.92 Å的碳原子之间的相互作用[26-27]。为了避免有限尺寸影响模拟结果，本模拟中使用石墨烯片层面积为S=39.35 Å×51.12 Å。对垂直于晶界的方向(y轴)施加压应力，应变速率为0.001 ps-1，模拟模型沿y轴周期性变化。模拟过程都在常温常压下进行，所以本论文采用 Nose-Hoover等温等压(NPT)系综，温度为 300 K[28]。为了减小模拟误差，模拟过程的时间步长应小于原子振动周期的10%，故适合于碳纳米管和石墨烯模拟的时间步长设为0.5~0.8 fs[25]。本实验采用常使用的0.5 fs的时间步长。

2 石墨烯晶界结构

将石墨烯沿x轴方向分为均等的两个部分，分别旋转一定角度，再连接起来，连接起来不再是完美的六元环，而是由五元环、七元环等形成的晶界。因此，石墨烯晶界可以通过晶向偏转角来定义：θ=θU+θD(其中θU和θD分别为上下两部分旋转的角度)。当θU=θD时，形成对称倾斜晶界。由于对称倾斜晶界的取向角不同，所以晶界的类型和密度不一样。如图 1所示是本论文中研究的4种晶界类型。YAZYEV等[15]的实验结果表明，21.8°和32.2°两种晶界的石墨烯能量都很低。LIU等[16]的研究证明，晶界角为38.2°的晶界的形成能较低，并且能在自然界中稳定存在。研究表明[29]，60°晶界的形成能比其他晶界的都要低。晶界角为 21.8°和 38.2°晶界是由一个五元环和一个七元环组成的链状结构。通常五元环和七元环缺陷在石墨烯内部会使其能量升高，但是晶界角为 60°的晶界对石墨烯的形成能影响很小；晶界是石墨烯不同晶向的典型接触面。图1所示为本研究中的4种对称倾斜晶界和完美石墨烯的模型。由图1可以看到，不同晶界角对应的晶界的形状也不一样。

图 2 压应力条件下不同晶界角晶界石墨烯的弯曲侧视图及压应力条件下不同晶界角晶界石墨烯的弯曲正视图以及本研究中石墨烯的弯曲曲线Fig. 2 Front view snap shots of different GB buckled graphene under free lateral boundary condition((a1)-(e1)) and lateral view of graphene with different grain boundary under compressive stress((a2)-(e2)) and bending curves of different buckled graphene of this study(f) (Black curves represent distance of y-deviation averaged over z-direction)

3 结果与讨论

3.1 不同晶界的石墨烯在压应力条件下的变形行为

模拟结果表明，在弛豫过程中石墨烯沿着厚度(z轴)方向波动，其形状不再是一个平整的平面。二维材料一直被认为是假设性的结构，无法单独稳定存在于自然界，但对于很薄有轻微波动的纳米级材料，可以认为这就是二维材料在自然界的存在状态。沿着压缩方向，石墨烯经过一定的压缩过程后开始弯曲变形，其变形情况跟其内部晶界有很大的关系。图2(a1)、(b1)、(c1)、(d1)、(e1)示分别为4种晶界的石墨烯与完美石墨烯在应变为0.4状态下的压缩变形情况；图2(a2)、(b2)、(c2)、(d2)、(e2)所示分别为 4种晶界和完美石墨烯压缩完成后的正视图；图3所示为4种晶界和完美石墨烯压缩过程的应力应变曲线。应变的计算公式为：ε=Δy/y0(其中Δy为石墨烯的压缩量，y0为石墨烯的厚度)。由图2可知，完美石墨烯在压应力下的弯曲形状类似正弦波，有晶界的石墨烯的变形形状类似拱桥形；但在相同应变条件下，含晶界的石墨烯的弯曲程度比完美石墨烯大很多。由图 3(e)可以看出，完美石墨烯在压缩过程中反向弹力很小，相对于含晶界的石墨烯在0 GPa附近的波动，完美石墨烯的强度高出20 GPa，在10 GPa左右发生波动。从图2(f)可以看出，石墨烯在晶界处的弯曲半径比完美石墨烯的大很多；且图2(c1)、(d1)中两种晶界的石墨烯在晶界处的弯曲程度比其他石墨烯的更大。由图2可知，有晶界的石墨烯在压应力下的弯曲发生在晶界处，而完美石墨烯的弯曲发生在石墨烯的上端。从图3(a)和(b)可以看出，压缩过程中这两种晶界的石墨烯压缩应力的幅度在变大，压力也在增大；从图3(c)、(d)、(e)可以看出，压应力增大幅度比图3(a)和(b)中两种石墨烯的小，且压应力的震动幅度也小很多；完美石墨烯的压应力比含晶界石墨烯的大很多，且压应力的变化幅度也小很多；可见完美石墨烯抵抗外界压力的能力比含晶界石墨烯的强，并且强度也更稳定。晶界的存在改变了石墨烯的原子排布情况，使其内部结构不稳定；在压应力条件下，由于各石墨烯薄片内部碳碳键的方向不同，所以其受力情况不一样，并且晶界处五元环和七元环的强度不如六元环的高，从而在压缩过程中，晶界处容易出现失稳，导致石墨烯晶界处弯曲变形大并且各晶界的石墨烯弯曲变形也不同。由此可见，晶界对石墨烯的变形行为有很大的影响。

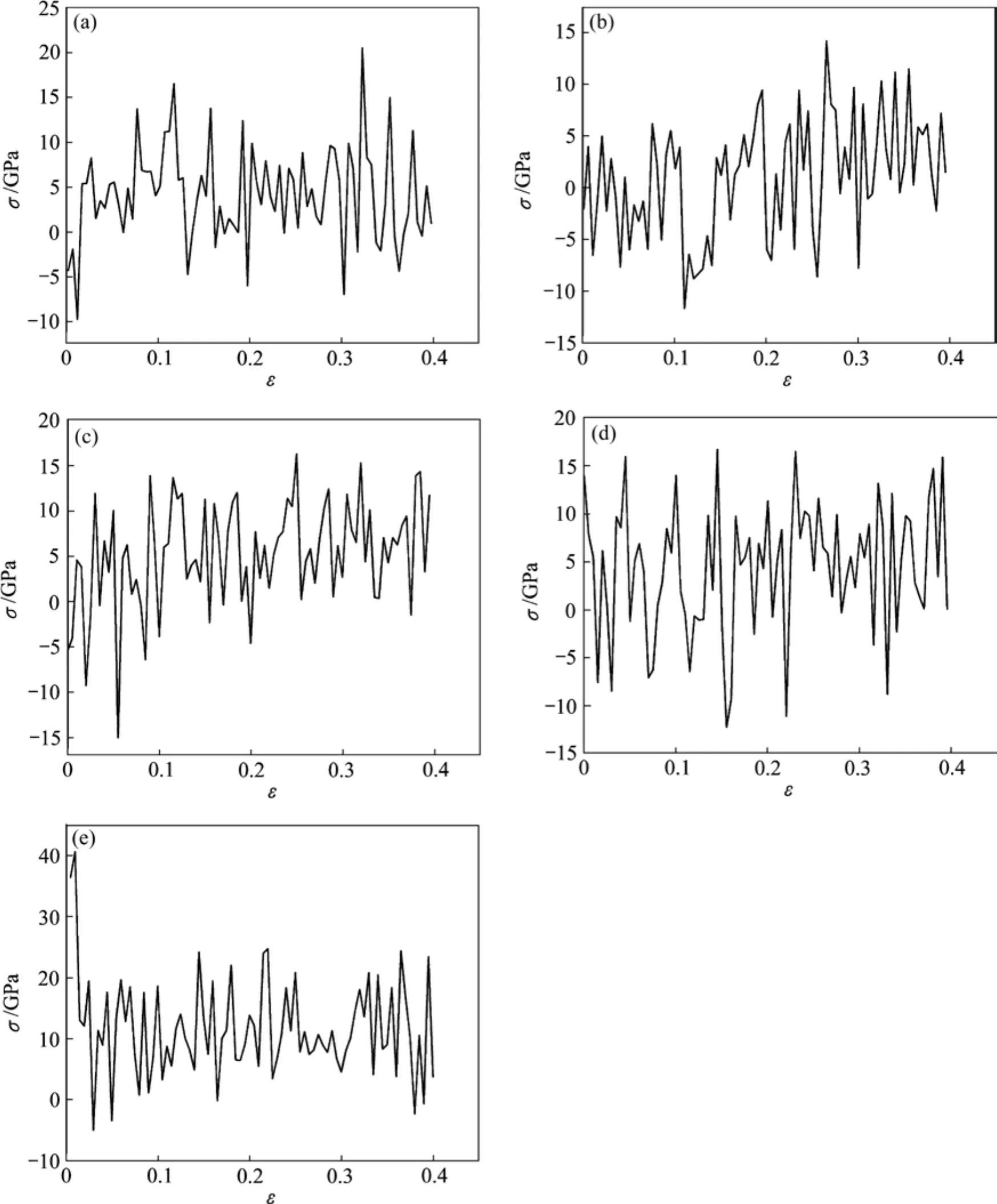
图 3 压应力条件下各石墨烯的应力-应变曲线Fig. 3 Stress-strain curves of different graphene nanoribbons under compressive stress: (a) 21.8°; (b) 32.2°; (c) 38.2°; (d) 60°;(e) Perfect graphene

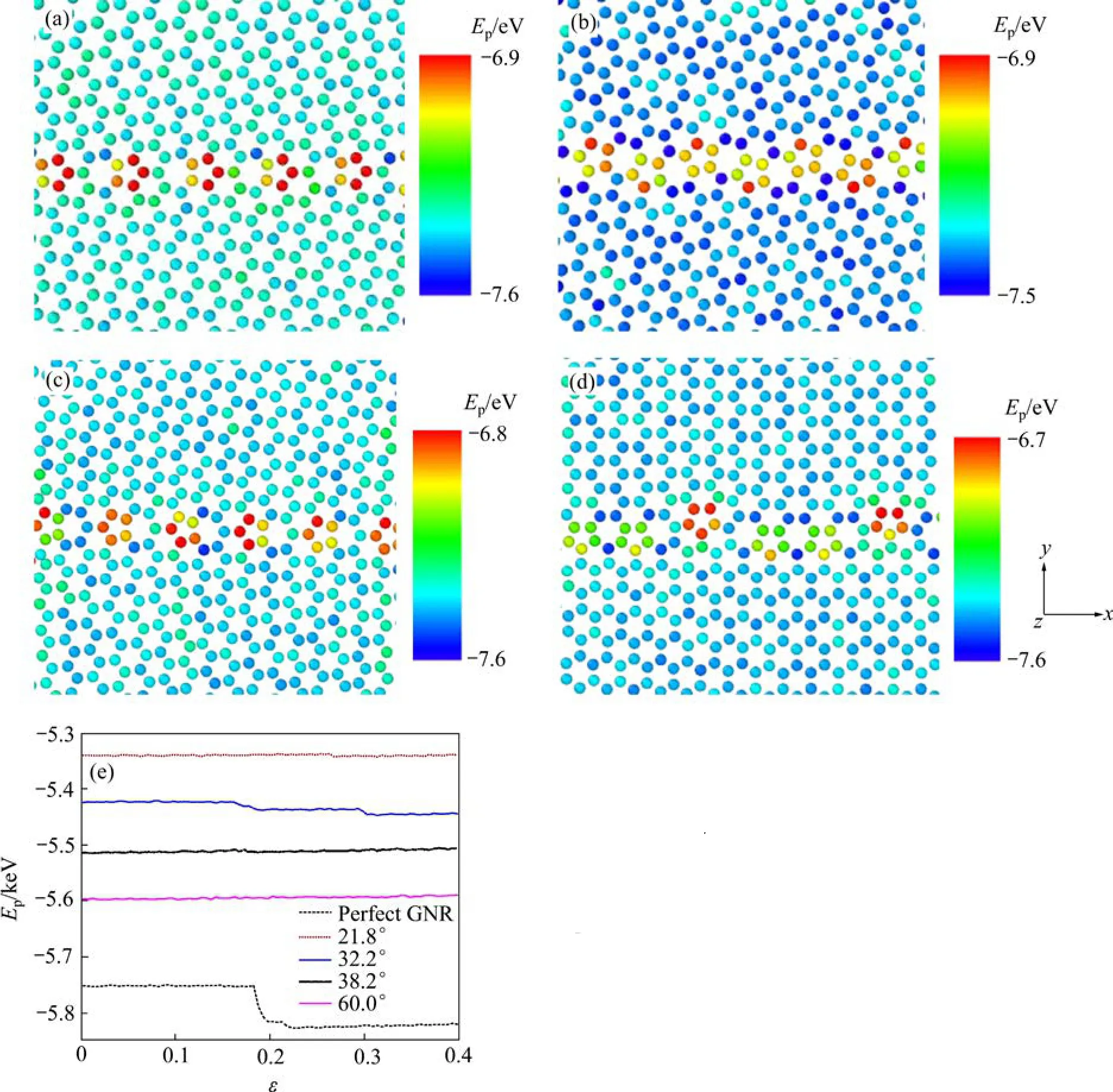
图4 经300 K弛豫后不同晶界石墨烯和完美石墨烯的势能分布图以及石墨烯在整个压缩过程中总势能的变化图Fig. 4 Four snap shots taken from central portion of GNRs with different GBs after relaxation at 300 K((a)-(d)) and graphene nanoribbons’ potential energy(e): (a) 21.8°; (b) 32.2°; (c) 38.2°; (d) 60°; (e)Graphene nanoribbons’ potential energy

3.2 势能的分布

石墨烯的势能可以通过原子模拟的方法和第一性原理或经验势函数给出。为了更好地揭示二维材料石墨烯的独特性能，考虑其平面和自由状态。根据第一性原理计算以角度θ为自变量的单原子势能r的函数，石墨烯晶界势能与形成能呈线性关系：r(θ)=Efθ/|b|(其中Ef为晶界形成能；b为晶界柏氏矢量)。图4所示为经300 K弛豫后不同晶界石墨烯和完美石墨烯的势能分布图以及石墨烯在整个压缩过程中总势能的变化图。由图4可知，包含有图4(a)和4(b)中所示晶界的石墨烯的势能比含有图 4(c)和4(d)所示的晶界的高，并且晶界处的势能明显比完美石墨烯的高，晶界处五元环的势能比七元环的高；含有图4(d)所示晶界的石墨烯势能比包含其他晶界的石墨烯略高。由图4可以看出，完美石墨烯的势能比有晶界石墨烯的低，随着模拟过程的进行，势能会出现轻微的波动，但是当应变达到0.18时，完美石墨烯的势能急剧下降，在后续的压缩过程中势能有上升的趋势。石墨烯(见图4(a)、4(c)、4(d))在压缩模拟过程中，势能呈上升趋势。石墨烯(见图 4(b))在压缩过程中势能下降两次，但下降的幅度都很小，不超过10 eV。由此可见，包含小角度晶界石墨烯的势能比含大角度晶界石墨烯的大，所有这些晶界的石墨烯都能在自然界稳定的存在。包含有晶界的石墨烯的总势能比完美石墨烯的高，因为晶界是石墨烯结构中的一种缺陷，缺陷的存在会改变石墨烯内部原子初始的排布，不规则排列的原子之间存在着一定程度的相互作用，从而结构内部的势能也会增大。原子不规则程度和排列方式的不同，都会改变石墨烯势能的大小。这也意味着热力学因素对石墨烯的结构和性能起着相当重要的作用。

图 5 不同晶界的石墨烯在压缩过程中的旋转分布(色条表示石墨烯沿z轴方向的旋转量)Fig. 5 Rotating distribution of graphene with different grain boundaries under compressive stress (Color bar indicates degree of graphene buckling away from axis z): (a) 21.8°; (b) 32.2°; (c) 38.2°; (d) 60°;(e) Perfect graphene

3.3 压应力下石墨烯的旋转变形

对矩形薄片状材料施加长度方向上的压应力，由于材料在压缩过程中的不均匀变形，会使其沿着厚度方向弯曲的同时沿着另一个方向发生旋转。图5所示为不同晶界的石墨烯在压缩过程中的旋转分布。由图5可看到5种石墨烯压缩完成时的旋转图，完美石墨烯在压缩过程中没有发生旋转(见图5(e))，而有晶界的石墨烯都有不同程度的旋转(见图5(a)、(b)、(c)、(d))。图 5(c)所示的石墨烯在压缩过程中旋转角度最大，其他有晶界的石墨烯旋转的角度很小，但是与完美石墨烯相比还是有明显的变化。晶界是由晶粒生长过程中各晶粒间取向差异所致，对称倾斜晶界的石墨烯是由两片完美石墨烯沿相反方向旋转相同角度后得到的；晶界的存在使石墨烯内部碳原子取向不同，且晶界处的碳碳键长与单晶石墨烯的不同。压应力条件下，晶界处碳原子的不规则排列使石墨烯受力不均匀，发生不同程度的弯曲和旋转。

3.4 压应力下不同层数石墨烯的弯曲变形

图 6所示为不同层数完美石墨烯(多层石墨烯各层石墨烯排列方式都相同，原子排列结构也相同)在压缩完成时的弯曲形状。从图6(a)~(c)可以看出，随着石墨烯层数的增加，弯曲中心沿y轴上移，并且外层石墨烯的弯曲半径比内层的大。随着石墨烯层数的增加，在压缩的过程中，会发生聚集的现象。当石墨烯层数为8层时，其最大的聚集层数为4层；而其他的大于2层石墨烯的最大聚集层数为3层。石墨烯内部碳原子的4个共价键只有3个键共价，另一个键处于自由状态的碳原子会对其他碳原子有力的作用；随着层数的增加，层与层之间的排斥力会增大，9层的石墨烯在压缩完成时，层与层之间的距离比其他层数的石墨烯的都大。在石墨烯内部，碳原子的4个共价键没有完全发生共价，共价的碳原子对邻近的石墨烯片会有力的作用。压力增加的过程随着石墨烯层数的增加，石墨烯不是单层弯曲，而是多层聚集弯曲。多层石墨烯各聚集团之间由于碳原子之间排斥力的作用，使聚集团之间的距离增大至聚集团之间无相互作用，各聚集团自由弯曲与相邻聚集团无相互影响，弯曲形状各不相同。

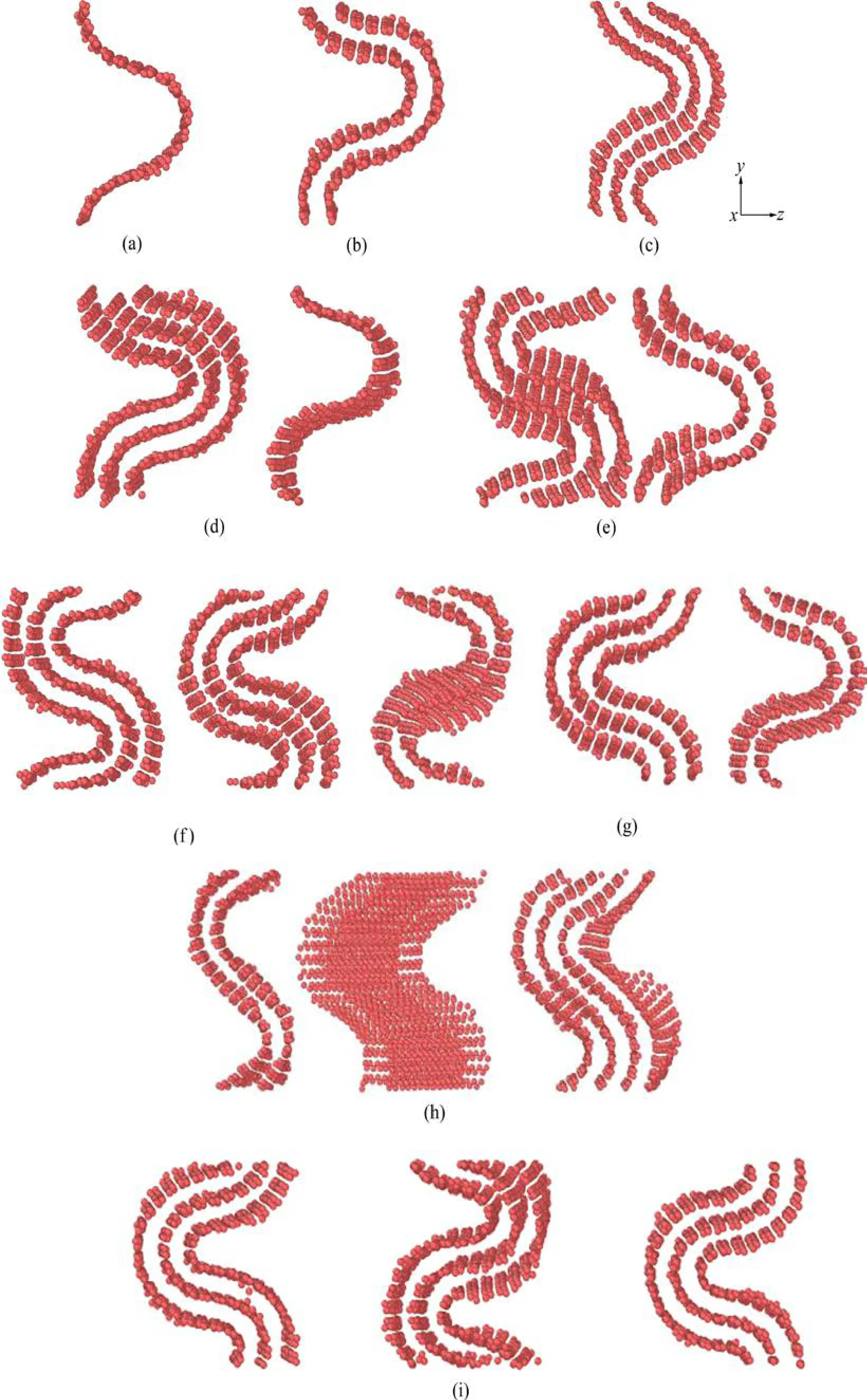
图6 压应力条件下1~9层完美石墨烯的弯曲变形Fig. 6 Bending deformation of 1-9 layers graphene nanoribbons’ shape after uniaxial compression along y axes under compressive stress: (a) 1 layer; (b) 2 layers; (c) 3 layers; (d) 4 layers; (e) 5 layers; (f) 6 layers; (g) 7 layers; (h) 8 layers; (i) 9 layers

4 结论

1) 采用 4种不同晶界的石墨烯与完美石墨烯进行对比，分析在压应力的条件下，石墨烯的弯曲变形。发现有晶界石墨烯的弯曲程度比完美石墨烯的大，有晶界的石墨烯在晶界处(石墨烯片层中间)弯曲，并且完美石墨烯的弯曲弧不在石墨烯片层的中间；不同晶界角对弯曲弧度的影响不大。

2) 晶界处的势能比完美石墨烯的大，有晶界的总势能比完美石墨烯的大。多层完美石墨烯在压应力下的变形行为也不尽相同，除了8层石墨烯的最大聚集层数为4；3~9层石墨烯的最大聚集层数都为3层。

[1] ALLEN M J, TUNG V C, KANER R B. Honeycomb carbon: A review of graphene[J]. Chemical Reviews, 2010, 110: 132-145.

[2] NOVOSELOV K S, GEIM A K, MOROZOV S V, JIANG D,ZHANG Y, DUBONOS S V, GRIGORIEVA I V, FIRSOV A A.Electric field effect in atomically thin carbon films[J]. Science,2004, 306(5696): 666-669.

[3] GEIM A K. Graphene: Status and prospects[J]. Science, 2009,324(5934): 1530-1534.

[4] LI Xue-song, CAI Wei-wei, AN Jin-ho, KIM S, NAH J, YANG Dong-xing, PINER R, VELAMAKANNI A, JUNG I, TUTUC E,BANERJEE S K, COLOMBO L, RUOFF R S. Large-area synthesis of high-quality and uniform graphene films on copper foils[J]. Science, 2009, 324(5932): 1312-1314.

[5] DOU Yuan-yun, LUO Min, LIANG Sen, ZHANG Xue-ling,DING Xiao-yi, LIANG Bin. Flexible free-standing graphene-like film electrode for supercapacitors by electrophoretic deposition and electrochemical reduction[J]. Transactions of Nonferrous Metals Society of China, 2014, 24(5): 1425-1433.

[6] LENG Xian, XIONG Xiang, ZOU Jian-peng. Rapid microwave irradiation fast preparation and characterization of few-layer graphenes[J]. Transactions of Nonferrous Metals Society of China, 2014, 24(1): 177-183.

[7] 王永祯, 王 勇, 刘志涛, 蔡晓岚. 石墨烯透明导电薄膜的合成与表征[J]. 中国有色金属学报, 2014, 24(7): 1817-1822.WANG Yong-zhen, WANG Yong, LIU Zhi-tao, CAI Xiao-lan.Synthesis and characterization of graphene transparent conductive films[J]. The Chinese Journal of Nonferrous Metals,2014, 24(7): 1817-1822.

[8] KIM K, LEE Z, REGAN W, KISIELOWSKI C, CROMMIE M F,ZETTL A. Grain boundary mapping in polycrystalline graphene[J]. ACS Nano, 2011, 5(3): 2142-2146.

[9] 曾 亭, 吴革明, 赵鸿滨, 杨萌萌, 魏 峰, 杜 军. 低压化学气相沉积生长双层石墨烯及其点运输特性研究[J]. 稀有金属, 2013, 37(4): 583-589.ZENG Ting, WU Ge-ming, ZHAO Hong-bing, YANG Meng-meng, WEI Feng, DU Jun. Low pressure chemical vapor deposition synthesis and transport properties of graphene[J].Chinese Journal of Rare Metals, 2013, 37(4): 583-589.

[10] 韩同伟, 贺鹏飞, 王 健, 吴艾辉. 空位缺陷对单层石墨烯拉伸力学性能的影响[J]. 同济大学学报(自然科学版), 2010,38(8): 1210-1214.HAN Tong-wei, HE Peng-fei, WANG Jian, WU Ai-hui. Effect of vacancy defects on tensile mechanical properties of single graphene sheets[J]. Journal of Tongji University (Natural Science), 2010, 38(8): 1210-1214.

[11] YU Qing-kai, JAUREGUI Luis A, WU Wei, COLBY Robert,TIAN Ji-fa, SU Zhi-hua, CAO He-lin, LIU Zhi-hong, PANDEY Deepak, WEI Dong-guang, CHUNG Ting-fung, PENG Peng,GUISINGER N P, STACH E A, BAO Ji-ming, PEI Shin-shem,CHEN Yong P. Control and characterization of individual grains and grain boundaries in graphene grown by chemical vapour deposition[J]. Nature Materials, 2011, 10(6): 443-449.

[12] SIMONIS P, GOFFAUX C, THIRY P A,BIRO L P, LAMBIN P H, MEUNIER V. STM study of a grain boundary in graphite[J].Surface Science, 2002, 511(1/3): 319-322.

[13] TISON Y, LAGOUTE J, REPAIN V, CHACON C, GIRARD Y,JOUCKEN F, SPORKEN R. GARGIULO F, YAZYEV O V,ROUSSET S. Grain boundaries in graphene on SiC(0001)Substrate[J]. Nano Letters, 2014, 14(11): 6382-6386.

[14] LEE Gun-do, YOON Euijoon, WANG Cai-zhuang, HO Kai-ming. Atomistic processes of grain boundary motion and annihilation in graphene[J]. Journal of Physics Condensed Matter, 2013, 25(15): 1-6.

[15] YAZYEV O V, LOUIE S G. Topological defects in graphene:Dislocations and grain boundaries[J]. Mesoscale and Nanoscale Physics, 2010, 81(19): 195420-1-7.

[16] LIU Te-huan, PAO Chun-wei, Chang Chien-cheng. Effects of dislocation densities and distributions on graphene grain boundary failure strengths from atomistic simulations[J]. Carbon,2012, 50(10): 3465-3472.

[17] NEEK-AMAL M, PEETERS F M. Buckled circular monolayer graphene: A graphene nano-bowl[J]. Journal of Physics-Condensed Matter, 2011, 23(4): 1-8.

[18] NEEK-AMAL M, PEETERS F M. Defected graphene nanoribbons under axial compression[J]. Applied Physics Letters,2010, 97(15): 11747-4502.

[19] NEEK-AMAL M, PEETERS F M. Effect of grain boundary on the buckling of graphene nanoribbons[J]. Applied Physics Letters, 2012, 100(10): 101905-1-4.

[20] FRANK O, TSOUKLERI G, PARTHENIOS J, PAPAGELIS K,RIAZ I, JALIL R, NOVOSELOV K S, GALIOTIS C.Compression behavior of single-layer graphene[J]. ACS Nano,2010, 4(6): 3131-3138.

[21] GALASHEV A E, DUBOVIK S Y. Molecular dynamics simulation of compression of single-layer graphene[J]. Physics of the Solid State, 2013, 55(9): 1976-1983.

[22] GAN Yang, CHU Wu-yang, QIAO Li-jie. STM investigation on interaction between superstructure and grain boundary in graphite[J]. Surface Science, 2003, 539(1/3): 120-128.

[23] YAKOBSON B I, DING Feng. Observational geology of graphene at the nanoscale[J]. ACS Nano, 2011, 5(3): 1569-1574.

[24] BELYTSCHKO T, XIAO Shao-ping, SCHATZ G C, RUOFF R S. Atomistic simulations of nanotube fracture [J]. Physical Review B, 2002, 65(23): 1-12.

[25] DEWAPRIYA N W, PHANI A S, RAJAPAKSE R. Influence of temperature and free edges on the mechanical properties of graphene[J]. Modelling & Simulation in Materials Science and Engineering, 2013, 21(6): 1-15.

[26] BRENNER D W. Empirical potential for hydrocarbons for use in simulating the chemical vapor deposition of diamond films[J].Physical Review B, 1990, 42(15): 9458-9471.

[27] GRANTAB R, SHENOY V B, RUOFF R S. Anomalous strength characteristics of tilt grain boundaries in graphene[J]. Science,2010, 330(6006): 946-948.

[28] FASOLINO A, LOS J H, KATSNELSON M I. Intrinsic ripples in graphene[J]. Nature Materials, 2007, 6(11): 858-861.

[29] LI Zheng-lu, LI Zhi-ming, CAO Hai-yuan, YANG Ji-hui, SHU Qiang, ZHANG Yue-yu, XIANG H J, GONG X G. What are grain boundary structures in graphene[J]. Nanoscale, 2014, 6(8):4309-4315.