一种改进的可变步长LMS算法及性能分析*

2015-03-25张炳婷赵建平刘凤霞

通信技术 2015年11期

关键词：均方步长稳态

张炳婷，赵建平，刘凤霞

(曲阜师范大学物理工程学院,山东曲阜 273165 )

一种改进的可变步长LMS算法及性能分析*

张炳婷，赵建平，刘凤霞

(曲阜师范大学物理工程学院,山东曲阜 273165 )

为解决自适应算法的收敛速度和稳态误差两者间的矛盾，对归一化的最小均方(NLMS)算法、变步长算法及可变步长NVSS算法进行了研究，并结合变步长的思想，提出了一种新的可变步长算法。新的算法中引入合适的遗忘因子与修正参数来建立与步长因子间的函数关系，加快了算法收敛速度的同时，也能在非平稳的环境中有好的跟踪能力。最后把不同的算法应用到系统辨识系统中，通过MATLAB进行实验仿真，结果证实了新提出的算法有快的收敛速度和跟踪时变系统的能力。

NVSS算法；变步长；系统辨识；收敛速度；跟踪能力

0 引言

目前基于最小均方误差LMS(Least Mean Square)算法的自适应滤波器，被广泛的用于系统辨识或系统建模、自适应噪声对消、自适应天线系统、信号处理等多个领域，LMS算法最早是由Windrow和Hoff提出的[1]，是建立在维纳滤波器的基础上，通过自动的调节滤波器的权系数，使滤波器的实际期望信号与已知输入信号间的误差达到最小。但在具体的应用中，始终存在着收敛速度和稳态误差这两者间的矛盾，随着研究者的进一步的研究，多种的改进的变步长被提出来解决这一矛盾。在时域上主要归结为两个方面的改进，一个方面是用误差来控制迭代步长，另一个方面是利用梯度向量来控制步长。最终是算法在初始的收敛阶段选取大的步长，在达到稳态时采用小的步长，来达到低的稳态误差[2]。本文主要研究了改进算法的具体改进方式，分析了变步长NLMS算法、NVSS算法、λNVSS算法及改进的算法在系统辨识应用中的性能。

1 NLMS算法

1.1 传统的NLMS算法

传统归一化的最小均方误差(NLMS)算法，是在基本的LMS算法的基础上，对步长进行了归一化的处理[3]，解决了当输入功率过大时引起的大的误差变化，降低了算法对梯度噪声的敏感度，减小了稳态误差，提高了收敛速度。具体的NLMS算法的相关表达式如下：

y(n)=w(n)Tx(n)

(1)

e(n)=d(n)-y(n)

(2)

w(n+1)=w(n)+u(n)e(n)x(n)T

(3)

(4)

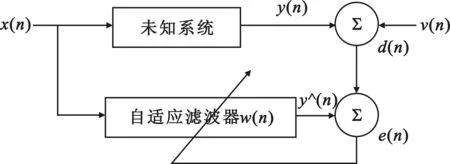
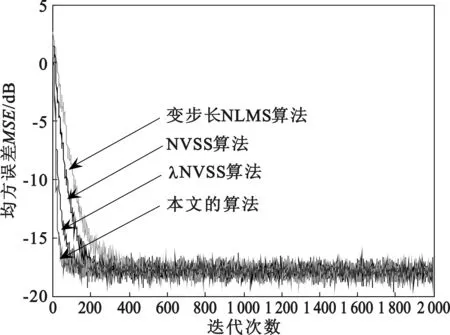
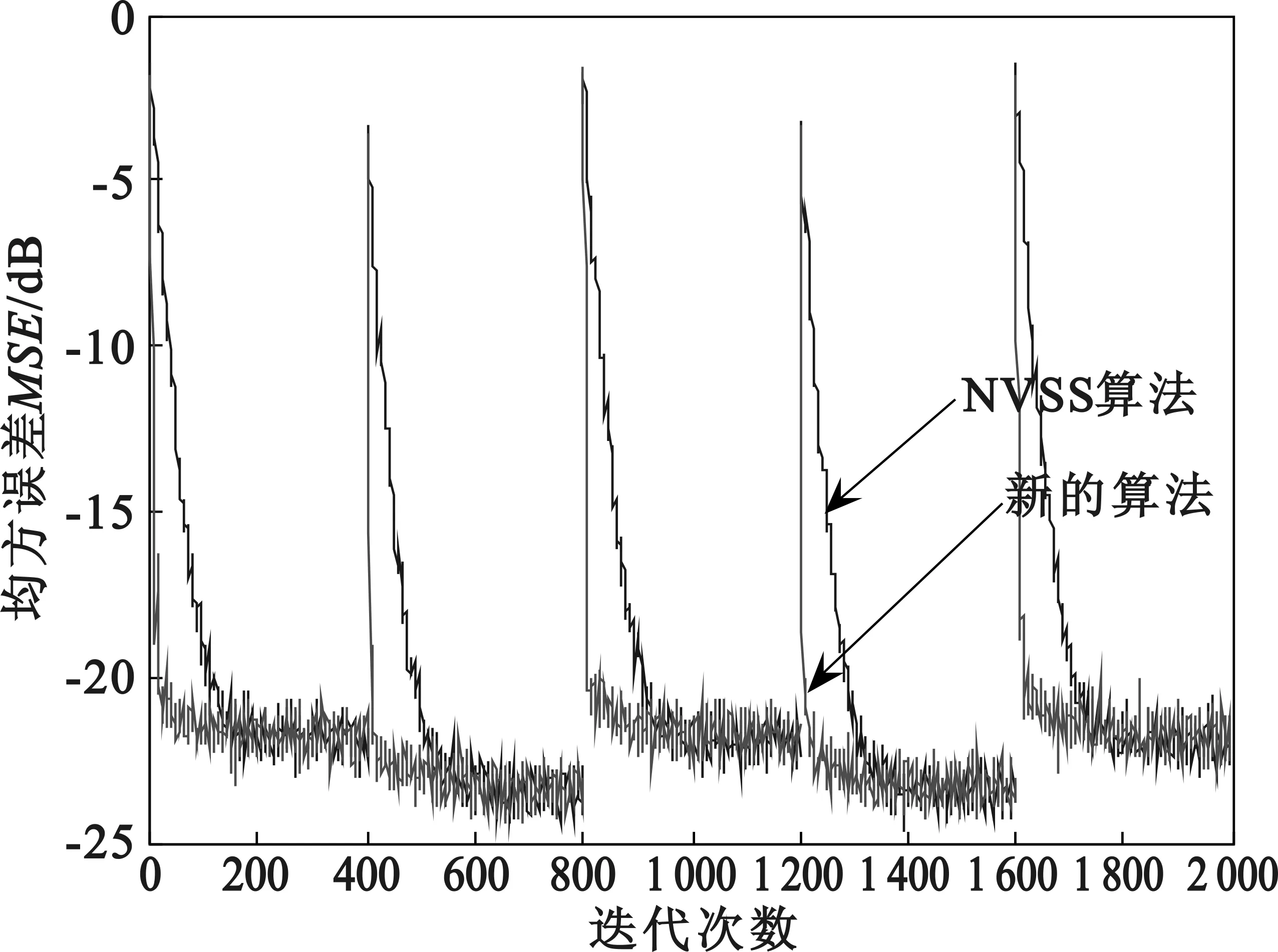
式中，x(n)是已知的输入信号,d(n)是期望响应的输出信号,y(n)则是实际的输出信号,w(n)是滤波器的抽头系数。e(n)是误差信号。式(3)是抽头权向量的递推公式，u(n)是步长因子，当满足0

J(n)=E{|e(n)|2}=E{|d(n)-y(n)|2}

(5)

即使滤波器的期望信号与实际滤波器的输出信号间的误差最小。此时的稳态误差作为衡量算法的一个性能指标。而算法的收敛速度则受步长大小的控制，是衡量算法的另一个重要标准。在满足收敛条件时，步长越大，收敛速度越快，但相应的稳态误差也越大；步长越小，稳态误差小，但相应的收敛速度减慢。对于算法在不同的应用中，稳态误差和收敛速度始终是衡量算法性能好坏的两个最重要的标准。但NLMS算法的步长是一定值，当步长固定时，容易取得局部最优，稳态误差和收敛速度不能同时满足[4]。

1.2 变步长NLMS算法

文献[5]中针对NLMS算法的不足之处，提出了变步长的NLMS算法。

该算法的步长表达式：

u(n)=β[1-exp(-α|e(n)e(n-1)|)]

(6)

权向量的更新表达式：

(7)

式中，0<α,0<β<1，0<γ的常数，防止分母为零。具体来说就是建立误差信号与步长因子间的函数对应关系，用当前的误差信号e(n)和前一时刻的误差信号的e(n-1)乘积来调节步长的变化来，这样进一步降低了算法对噪声的敏感度。同时使算法在开始的收敛阶段采用大的步长来加快收敛速度，达到稳态后使用小的步长来降低稳态误差。但是具体的效果并不明显，为进一步的解决这两者间的矛盾，更多的改进算法被提出。

1.3 NVSS算法

在文献[6]当中提出的改进的NVSS算法，其中步长的迭代公式为：

(8)

在文献[7]中提出的改进的λNVSS算法。将式(8)进一步的变形得到式(9)：

(9)

(10)

(11)

在式(10)中p>0看作是修正参数，M是滤波器的阶数，该算法通过修正系数p和遗忘因子λn，利用当前和过去的共M个误差控制步长的迭代变化，记为NVSS算法。

2 本文提出的算法

本文提出的算法在NVSS和λNVSS算法的基础上，受文献[5]中变步长NLMS算法步长因子的启发，尝试引入新的修正参数p和遗忘因子λn来控制步长的迭代过程。令λn=exp(-α|e(n)e(n-1)|)则此时权向量的迭代方程变为：

w(n+1)=w(n)+

(12)

式中，p>0,0<α<1。分析新的算法中，在平稳环境时，在算法的出初始阶段误差e(n)比较大，由于0<α则p/λn取得的值较小，迭代次数不多则‖e(n)‖2较小，此时步长较大。也就是在算法的初始阶段取得大的步长，随着迭代次数的增加‖e(n)‖2是逐渐变大的，而误差e(n)是逐渐变小的，即p/λn是变大的，则步长是减小的。通过仿真画出算法中步长因子u(n)随迭代次数变化时的图形。如图1所示，在算法的开始取得大的步长，随着迭代次数的增加，步长逐渐减小。从分析得知，这样算法有快的收敛速度时，也能获得低的稳态误差，相应的性能分析在文章的后半部分会进行验证。

图1 本文算法的步长随迭代次数的变化

而在非平稳的环境中，即系统发生跳变时，e(n)变化较大，而在算法的初始阶段p/λn起主要作用，它的变化是较小，从而拥有好的跟踪跃变能力。

3 算法在性能分析

3.1 系统辨识的分析

为了验证新算法的收敛速度、稳态误差和跟踪跳变系统的能力。将本文提出的新算法和变步长的NLMS、NVSS算法、λNVSS算法应用到系统辨识系统当中，用MATLAB来进行系统性能的仿真分析。系统辨识就是当给定一个未知的系统时，自适应滤波器通过反馈信息来调节自身的滤波器系数，当误差最小时，自适应滤波器就与未知系统有相似的特性，从而达到系统辨识的目的[8]。

图2是常见的系统辨识原理框图，为了方便实现仿真，假定自适应滤波器与未知系统两者的阶数是相同的。图2中x(n)是随机的输入信号,d(n)是由经未知系统后得到的输出信号y(n)与噪声信号v(n)叠加而成，其中v(n)是高斯白噪声，与输入信号x(n)不相关，误差信号e(n)是滤波器的输出y∧(n)与d(n)间的差值。它们之间的对应运算关系如下：

(13)

d(n)=y(n)+v(n)

(14)

y∧(n)=WT(n)X(n)

(15)

e(n)=d(n)-y∧(n)

(16)

W(n+1)=w(n)+

(17)

算法经过多次迭代运算，当误差信号e(n)最小时，自适应滤波器的权系数近似于未知系统的滤波器系数，也就达到了系统辨识的目的。

图2 系统辨识原理框

3.2 稳态环境下不同算法的性能分析

将变步长算法NLMS、NVSS算法、λNVSS和本文提出的算法应用到上述的系统辨识中，要测量的未知系统是4阶的横向滤波器。设定测量的输入信号与测量的噪声信号的信噪比是20 dB。把自适应滤波器的权系数设定为Hn=[0.8783 -0.5806 0.6537 -0.3223]。在进行具体的应用环境中，相应的参数都取相应的最佳值，变步长算法NLMS中β=0.08、α=20，NVSS算法中，步长u取0.04，λNVSS中p=5,在本文提出的算法中α=0.8、p=1。不同的算法都做200次的独立仿真，并求平均值，得到学习曲线的仿真结果如图3所示。

图3 不同算法的学习曲线比较

从图3中可以清楚地看到，在相同的信噪比下，不同算法都有低的稳态误差，但是就收敛速度而言，文献[7]中的λNVSS算法，要比变步长NLMS算法和文献[6]中NVSS算法的收敛速度快，而本文中提出的算法与这3种算法相比，有更快的收敛速度。因此本文提出的新的算法在没有增加稳态误差的前提下，同时明显的提高了收敛速度。

3.3 跟踪跳变系统的性能分析

上述仅是验证了新的算法在稳态环境中的快的收敛速度，在非稳态环境中时算法的跟踪能力需要进一步的验证。因此为了验证本文算法的跟踪时变系统的能力，定义未知系统的初始值Hn=[0.8 0.5]，在第400个采样点系统跳变为 Hn=[0.4 0.2]，在第800,1 200,1 600个采样点处依次跳变。采用NVSS算法和新提出的算法进行仿真，在NVSS算法中步长u取0.04，新提出的算法中p=1、α=0.8。图4是算法运行200次后取平均值得到的学习曲线。

通过比较可以看出系统发生跳变时，两种算法都有跟踪时变系统的能力，但是随着跳变次数的增加，算法的跟踪速度都有所减慢，但是本文算法的减慢速度要低于NVSS算法的减慢速度。因此，仿真证实本文提出的算法有好的跟踪跳变系统的能力。

图4 不同算法的学习曲线比较

4 结语

在归一化的最小均方(NLMS)算法和可变步长NVSS算法的基础上，结合变步长NLMS的变步长思想，通过引入新形式的遗忘因子来建立变步长表达式，从而提出新的算法。并将算法应用到系统辨识中，通过仿真实验证明了本文提出的算法有快的收敛速度、跟踪时变系统的能力和好的稳态误差。但是新的算法只是维持了原有的稳态误差，并没有做到进一步的减小稳态误差，在接下来的学习过程中要努力解决这个问题，并尝试把算法在硬件中实施。

[1] Widrow B, Mcool J M, Arimoer M G. Stationary and No Stationary Learning Characteristic of the LMS Adaptive Filter[J].ProcIEEE,1976,64(8):1151-1162.

[2] 李宁. LMS自适应滤波算法的收敛性能研究与应用[D].哈尔滨：哈尔滨工程大学，2009. LI Ning. Convergence Performance Analysis and Application of the Adaptive Lease Mean Square Algorithm [D].Harbin: Harbin Engineering University, 2009.

[3] 张琦,王霞,王磊等.自适应回波抵消中变步长NLMS算法 [J].数据采集与处理,2013,29(01):35-41. ZHANG Qi, WANG Xia, WANG Lei, etc. Variable Step Size NLMS Algorithms in Echo Cancellation [J]. Journal of Data Acquisition and Processing,2013,29(01):35-41.

[4] 韩冰，晋东立.数字预失真器模型参数辨识算法研究[J].通信技术，2015,48(07)：799-802. HAN Bing, JIN Dong-li. Parameters Identifications Algorithm of Digital Pre-Distorter Model [J]. Communications Technology, 2015,48(07)：799-802.

[5] 沈大伟，贺思，李正宙等.一种改进的变步长变更新速率LMS自适应滤波算法及仿真[J].电子质量,2010(12): 11-12. SHEN Da-wei，HE Si, LI Zheng-zhou, et al. A Modified Variable Step-Size and Multi-Rate Updated LMS Adaptive Filtering Algorithm and Its Simulation [J].Electronics Quality,2010(12):11-12.

[6] Zayed Ramadan. Alexander Poularikas. Performance Analysis of a New Variable Step-Size LMS Algorithm with Error Nonlinearities[A]. Southeastern Symposium on System[C]. America: Atlanta, IEEE Press,2004.384-388.

[7] 王伟强，杨金明，杨萍.一种新的可变步长LMS算法及性能分析[J].信息技术，2005,9(38)：117-122. WANG Wei-qiang, YANG Jin-ming, YANG Ping. Performance Analysis of a Novel Variable Step-Size LMS Algorithm[J]. Information Technology, 2005,9(38)：117-122.

[8] 李竹,杨培林,行小帅.一种改进的变步长LMS算法及其在系统辨识中的应用[J].仪器仪表学报，2007,28(07)：1340-1344. LI Zhu，YANG Pei-lin, HANG Xiao-shuai. Modified Variable Step-Size LMS Algorithm and Its Application in System Identification [J].Chinese Journal of Scientific Instrument, 2007,28(07)：1340-1344.

A Modified Variable Step-Size LMS Algorithm and Its Performance Analysis

ZHANG Bing-ting，ZHAO JIAN-ping，LIU Feng-xia

(College of Physics Engineering, Qufu Normal University, Qufu Shandong 273165, China )

To solve the contradiction of between convergence rate and steady-state error of adaptive algorithm, NLMS (Normalized Least Mean Square) algorithm, variable step algorithm and variable step NVSS algorithm are studied and researched, and in combination with the idea of variable step,a novel variable step-size algorithm is proposed. By introducing appropriate forgetting factor and correction parameters in this novel algorithm and establishing function relationship with between step factors,the convergence rate is accelerated and meanwhile, a fairly a good tracking ability in non-stationary environments maintained. Finally, different algorithms are applied in system identification, and MATLAB simulation indicates that the newly-proposed algorithm enjoys fairly fast convergence speed and tracking ability of time-varying systems.

NVSS algorithm; variable step size; system identification; convergence rate; tracking ability

10.3969/j.issn.1002-0802.2015.11.003

2015-06-02；

2015-09-20 Received date:2015-06-02；Revised date：2015-09-20

国家自然科学基金资助项目(No.11302118)；山东省自然科学基金资助(No.ZR2014FM011)；山东省高等学校科技计划项目资助(No.J12LN08)Foundation Item:National Natural Science Foundation of China(No.11302118);Natural Science Foundation of Shandong Province (No.ZR2014FM011);Science and Technology Project of Higher Education of Shandong Province(No.J12LN08)

TN929.5

1002-0802(2015)11-1217-05