基于双PID的旋转倒立摆控制系统设计与实现

刘二林，姜香菊

LIU Er-lin1, JIANG Xiang-ju2

（1. 兰州交通大学 机电工程学院，兰州 730070；2. 兰州交通大学 自动化与电气工程学院，兰州 730070）

0 引言

倒立摆是机器人技术、控制理论、计算机控制等多领域、多技术的有机结合，其控制系统本身是一个绝对不稳定、高阶次、多变量、强耦合的非线性系统，可以作为典型的控制对象对其进行研究。倒立摆的种类很多，有直线倒立摆、旋转倒立摆、平面倒立摆等。旋转倒立摆是三种形式的倒立摆中结构较简单的一种。相对于小车式的直线倒立摆而言，由于其将小车控制改为悬臂的旋转控制，其中间环节较少，机械结构较容易实现；但是其受力分析更加复杂，具有更大的非线性、不稳定及复杂性，对控制算法提出了更高的要求[1,2]。

论文中，采用直流电机，减速机构，微控制器，电机驱动芯片，1024线绝对式编码器等设计了一个一级旋转倒立摆；同时，利用拉格朗日方程对倒立摆进行了动力学分析，建立了系统完整的数学模型，并在MATLAB中采用双PID控制模式进行了控制器设计，并进行了仿真验证。最后，将设计的控制器移植到微控芯片中进行了实际测试，并将测试结果通过通讯模块上传至上位机进行了数据分析。结果表明，设计的系统机械结构合理，响应速度快，鲁棒性好。

1 旋转倒立摆基本结构

旋转倒立摆主要由倒立摆支撑机架、电机、减速装置、摆杆、旋臂、1024线位置式编码器、BT7960构成的H桥电路及微控制器芯片组成。倒立摆结构框图及实物图如图1所示。

图1 倒立摆结构及实物图

在图1(b)中，旋转倒立摆的旋臂与减速器的输出轴联接，减速器由直流电机驱动[3,4]，编码器1的齿轮与直流电机主轴齿轮啮合。通过获取编码器1的角度和角速度可以计算出旋臂的角度和角速度。编码器2安装在旋臂末端，且编码器2的旋转轴与旋臂的主轴平行；摆杆安装在编码器2的旋转轴上，摆杆轴线与编码器旋转轴垂直。系统中，旋臂只能以减速器动力输出轴为圆心做水平旋转，摆杆只能以编码器2旋转轴为圆心在旋臂末端旋转轨迹的切面上做竖直旋转。

2 旋转倒立摆数学模型

对旋转倒立摆进行受力分析，建立广义坐标系。系统的简化模型如图2所示。利用拉格朗日方程建立系统的运动学微分方程[1,5～8]。

由图2可知，系统中摆杆与旋臂各有一个自由度，所以，可以取α和θ为广义坐标。则倒立摆系统的动能由四部分组成。

其中T1为旋臂的转动动能，T2为摆杆的转动动能，T3为摆杆沿X轴方向运动的动能，T4为摆杆沿Y轴方向运动的动能，

因为α→0，所以sin α→0，cos α →1，将式1各项进行计算合并，并且对其进行线性化处理可得：

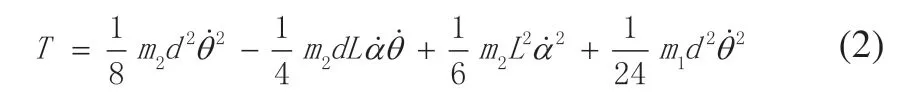
图2 系统简化模型

由式(3)可得：

式 (5) 中，Tout为电机输出扭矩 ，

由式(4)可得：

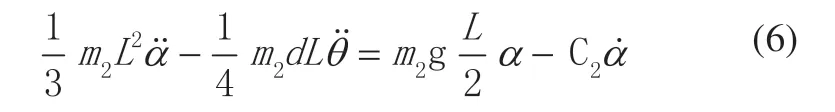
将式(4)、式(5)联立组成方程组，得到倒立摆系统线性化状态方程。

式(7)中：

以上各式中，参数的物理意义、数值及单位如表1所示。

3 旋转倒立摆控制器设计

旋转倒立摆的控制目标是：使倒立摆摆杆稳定在正上方，摆杆角度旋臂角速度或者使倒立摆在倒立的情况下匀速旋转。如果用传递函数对理想倒立摆系统进行分析，可以发现系统有一个极点在s平面的右半平面，系统不稳定。系统如果希望达到α→0的目标，可以通过PID控制器使系统的两个极点都位于s平面的左半平面，则倒立摆系统稳定[9～12]。

表1 状态方程中各参数列表

通过分析，为了使摆杆和悬臂都稳定在期望的位置，对旋臂和摆杆使用PID控制，在控制器中，PID控制器1对倒立摆摆杆的角度α进行控制，控制器输出为正反馈；PID控制器2对旋臂的角速度进行控制，控制器输出为负反馈。控制系统结构图如图6所示。

图3 双PID控制仿真系统结构图

在仿真过程中，取倒立摆模型的摆杆角度α的初始值为-0.175（约为10度），旋臂初始角度为0。取Kp1=100，Kd1=20，Ki1=1.5，取Kp2=2.2，Kd2=0.08，Ki2=0.01，PID2控制器输出的电压值限幅范围为：-5V～+5V，控制器总体输出的电压值限幅范围为：-10V～+10V，控制器输出部分的m文件如下：

图4 α=0，0时双PID仿真曲线

通过仿真曲线图可以看出，倒立摆系统的摆杆会稳定的停留在α=0处，但是由于摆杆初始角度的存在，同时PID控制器2控制的变量为摆杆的角速度且所以，旋臂会稳定在3rad附近。这与实际控制过程相符合。

通过仿真曲线可以看出，倒立摆旋臂会沿着设定的方向匀速旋转，摆杆的角度会略微偏离0角度，α≈2.1×10-3。这也与旋转倒立摆的实际运行曲线相符合。

4 旋转倒立摆实际运行数据分析

将Matlab中的控制算法移植到微控制器中，通过虚拟示波器将摆杆的角度及旋臂的角速度传到上位机中。上位机虚拟示波器显示的波形图如图6所示。

图6中，纵坐标为角度和角速度，对于角度而言，其单位为：

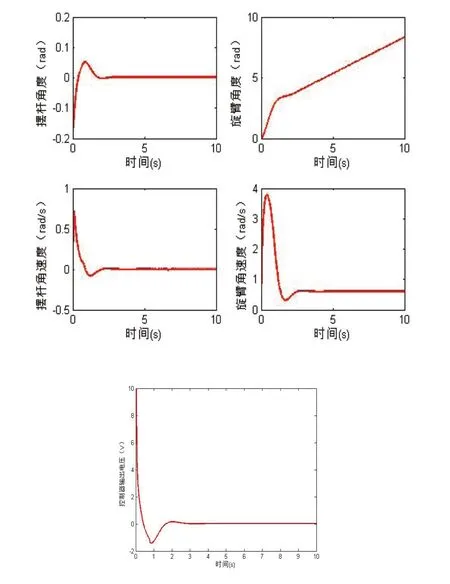
图5 α=0，时双PID仿真曲线

式中512为π所对应的分度值。

对于旋臂角速度而言，其单位为：

式中，512为π所对应的分度值，2.7为传感器齿轮与旋臂齿轮的齿数比，6×10-3为数据监测周期，周期单位为秒。

分析图6(a)可知，运行过程中，倒立摆摆杆一直在震荡，震荡中心线偏离计算中心0，这与倒立摆实际重心与传感器采样中心不重合有关，倒立摆摆动幅度大约在-6.13×10-2～+0.183rad之间。倒立摆旋臂速度有突变，这与电机齿轮与减速齿轮之间的间隙较大有关。这都是在制作实物时的结构不对称造成的。将摆杆处增加一高14cm，重量60g的重物，倒立摆运行波形图见图6(b)。由图6(b)可以看出，摆杆的高度及质量变化后，倒立摆运行依然正常，且系统更稳定。

图6 倒立摆运行波形图

5 结束语

论文的创新点在于：1）利用1024线绝对式编码器及其相关电子元件设计了一款简易旋转倒立摆。2）根据旋转倒立摆的实物，建立了与实际系统相符合的数学模型，并通过MATLAB用双PID控制器对模型进行了控制仿真。3）通过上位机，对实际运行数据进行了采集；通过数据分析，论述了仿真中的数据与实际运行结果差异的原因；并通过实验验证了所设计控制器的良好性能。

[1] 吴爱国,张小明,张钊.基于Lagrange方程建模的单级旋转倒立摆控制[J].中国工程科学,2005,7(10)：11-15.

[2] S.Awtar,N.King,T.Allen,I.Bang,M.Hanan,D.Skidmore,K.Craig. Inverted pendulum systems： rotary and arm-driven-a mechatronic system design case study[J].Mechatronics,2002,(12)：357-370.

[3] 张朝阳,魏晓赟,王少峰.基于52单片机的旋转倒立摆的研究和与设计[J].廊坊师范学院学报(自然科学版),2014,14(4)：49-52.

[4] Du Gaixin,Huang Nanchen, Wu Gang. The rotational invertedpendulum based on DSP controller[A].Proc of the 4th World Congress on Intelligent Control and Automation[C].China Shanghai,2002,7(4)：3101-3105.

[5] 宋君烈,肖军,徐心和.倒立摆系统的Lagrange方程建模与模糊控制[J].东北大学学报(自然科学版),2004,23(4)：333-337.

[6] 张欣.单级旋转倒立摆的二次型最优控制研究[J].电脑开发与应用,2011,24(12)：28-29,32.

[7] 丛爽,张冬军,魏衡华.单级倒立摆三种控制方法的对比研究[J].系统工程与电子技术,2001,23(11)：47-50.

[8] 姜倩,管凤旭.旋转式倒立摆的镇定和摆起控制[J].哈尔滨商业大学学报(自然科学版),2007,23(3)：232-234.

[9] 江晨,王富东.旋转式倒立摆系统的算法研究及仿真[J].工业控制计算机,2010,23(5) ：54-56.

[10] 陈进,王冠凌,邢景虎.单级倒立摆的PID和模糊控制对比研究[J].自动化与仪器仪表,2009,1423(2)：17-18.

[11] 曹敏,徐凌桦. 单神经元PID算法在倒立摆控制系统中的应用[J].微计算机信息,2009,25(1-1)：70-71.

[12] 杨平,徐春梅,曾婧婧,蒋式勤,彭道刚.PID控制在倒立摆实时控制系统中的应用[J].微计算机信息(测控自动化)2006,22(7-1)：83-85.