中心及带宽可调梳状线滤波器的设计

高 凡

GAO Fan

（桂林航天工业学院 电子工程系，桂林 541004）

0 引言

在滤波器中心频率调谐过程中，绝对带宽也跟着变化，但这一点以往却未受到足够重视。可是信道或者系统又要求绝对带宽不变。因此如何保持绝对带宽恒定成为近年来一个非常热门的研究方向。

I. C. Hunter 和 J. D. Rhodes在“Electronically Tunable Microwave Bandpass Filter”[1]中提出了控制绝对带宽的方法，谐振器长度为18.91mm的梳状线，只有10%的变化。Vikram Sekar等人在“A 1.2-1.6GHz Substrate-intergated-waveguide RF MEMS Tunable Filter”[2]中和El-Tanani, M. A.等人在“A 1.2-1.6GHz Substrate-intergated-waveguide RF MEMS Tunable Filter”[3]中利用交指耦合结构控制绝对带宽恒定。Ramesh Grag和I. J. Bahl在“Characteristics of Coupled Microstrip lines”[4]中，通过控制双模谐振器奇偶模谐振频率差保持绝对带宽恒定。Chih-Chieh Cheng和Rebeiz, G. M.在“High-Q 4-6-GHz Suspended Stripline RF MEMS Tunable Filter With Bandwidth Control”[5]中采用基于RF-MEMS技术的悬置微带线可以控制绝对带宽及保持恒定。Yuan Chun Li和Quan Xue在“Tunable Balanced Bandpass Filter With Constant Bandwidth and High Common-Mode Suppression”[6]中通过选择合适耦合区域和控制外部品质因数来保持滤波器绝对带宽恒定。Derek Scarbrough等人在“Miniature Microwave RF MEMS Tunable Waveguide Filter”[7]中采用波导作为谐振器保持滤波器绝对带宽恒定。Peng Wen Wong和Ian C. Hunter在“Electronically Reconfigurable Microwave Bandpass Filter”[8]中采用并联开关延迟线来保持滤波器绝对带宽恒定。要保持滤波器绝对带宽恒定需要解决两个核心关键问题：谐振器之间耦合系数与频率成反比、外部品质因数与频率成正比。

1 滤波器中心及带宽调节分析

1.1 耦合分析

二阶带通滤波器的耦合系数k12定义为：

g1和g2为基本元件值，来自于低通原型滤波器。要保持电调滤波器的绝对带宽在整个频率范围内不改变，FBW必须与频率成反比。所以耦合系数k12必须与频率成反比。

对于采用微带线耦合的谐振器来说，既存在磁耦合，也存在电耦合；可以由其电压、电流分布求得。磁耦合与频率成反比、电耦合与频率成正比。总的耦合系数为：

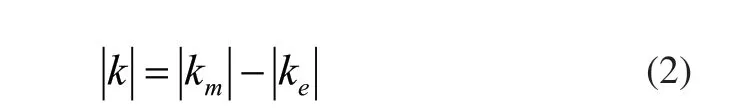
只要电耦合的强度小于磁耦合，总的耦合系数与磁耦合同极性。也就是说总的耦合系数随着频率的升高而减小，从而滤波器的绝对带宽保持不变。

二阶带通滤波器外部品质因数Qe为：

要保持电调滤波器的绝对带宽在整个频率范围内不改变，FBW必须与频率成反比。由上式可以得出外部Qe必须满足与频率成正比的要求。

1.2 滤波器的电调原理

通过调整谐振器的长度可以改变滤波器的中心频率。适当缩短谐振器的长度同时在谐振器的一端加载一个变容二极管，这样当二极管容值变化时滤波器的中心频率就跟着变化[9～13]。从其等效电路来分析，如图1所示[14]，终端开路的微带线等效为一个并联电容。

图1 终端开路微带线

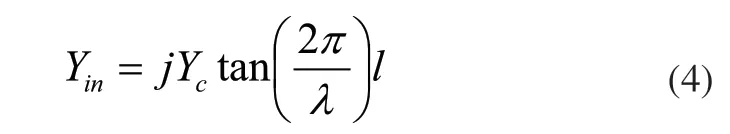
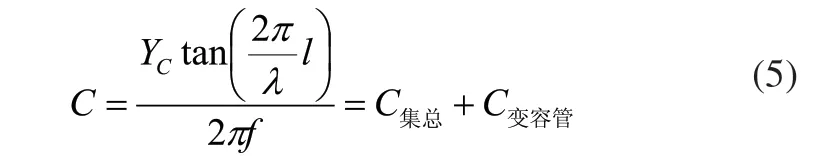
由此可见，当加在谐振器一端的电容值改变时，等效的谐振器长度也随着改变，即滤波器的中心频率也跟着改变。如图1所示，本设计采用变容二极管作为滤波器的电调部分，其电容值易于控制。只要变容二极管两端的电压值一改变，其电容值也跟着改变，最终电压调频得以实现。

2 中心及带宽可调梳状线滤波器的实现

本节将介绍一个梳状微带线电调滤波器的设计实例，该电调滤波器将在1.45GHz～1.89GHz频段上实现灵活的电压调频，并基本保持其带宽在100MHz不变。梳状电调滤波器的结构如图2所示。

图2 微带梳状电调滤波器结构

设计主要包括三个部分：1）由集总电容和微带线组成梳状线带通滤波器，包括计算集总电容的电容值和综合微带线尺寸；2）电压调谐，即把集总电容换成变容二极管，分析其如何影响滤波器特性；3）电源偏置滤波，通过滤出电源中的低频或高频噪声，一可以避免电源和射频信号的互相影响，二可以使电源电压稳定。

2.1 梳状线滤波器的设计

梳状线滤波器设计包括七步。第一步由带通滤波器的参数得到低通技术指标；第二步依据低通技术指标选定原型及阶数，选取相应的元件值；第三步利用Ansoft Designer软件进行滤波器设计，得到滤波器的结构初值；第四步利用ADS软件建立电路模型，并带入初值进行初步仿真观察结果；第五步设置优化参量和目标进行优化仿真，确定滤波器耦合节的长宽和间距；第六步选择不同的中心频率进行优化仿真，得到满足设计指标的不同的电容值，根据其变容范围选择变容管型号；第七步带入已选型号二极管的等效模型进行优化仿真并得到最终结果。

本次仿真使用波纹为0.1dB的3阶切比雪夫低通原型。基板选用F4BK，相对介电常数：εr=2.2；基板厚度：h=0.8mm；敷铜厚度：M=0.035mm。

为了确定应选的变容二极管的型号，选取了5个中心频率点进行优化仿真。优化得出的电容值如表1所示。

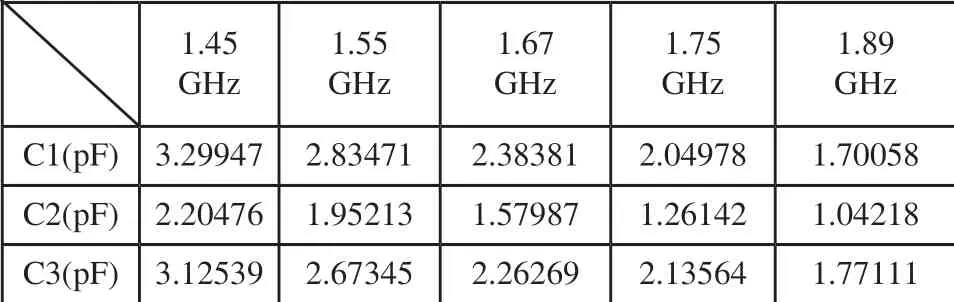
表1 各频点优化后集总电容值

根据表1中所得的集总电容值可得，变容管的可变电容值的范围大约在1.0pF～3.5pF之间。由此选择变容管SMV1408。该变容管在0V时的电容值为4.08pF，在30V时电容值为0.95pF。

此时各个频点的仿真结果如图3(a)～图3(e)所示。

图3 仿真结果1

从以上仿真结果可以看出，所选取的5个频点的带内插损、带外抑制和回波损耗都基本满足指标要求。证明本设计方法是可行的。下面将介绍滤波器偏置滤波的设计。

2.2 电源偏置滤波的设计

图4为电调部分的变容管模型及偏置滤波部分的ADS仿真图。由于ADS中提供的二极管模型有限，所以需要用二极管的等效电路模型带入电路进行仿真[15,16]。通过改变加在变容二极管上的反向电压来改变它的电容值。由于存在各种低频、高频噪声的干扰，实际的电源不能达到理想状态：电位在平面任何一点都不改变、阻抗为零。只有对电源进行滤波，才能保持电源稳定。滤波包括三部分：1）在电源两端并联一个去耦电容滤波；2）采用隔离直流电容可以克服直流电源对射频信号的影响；3）采用1/4波长的高阻抗传输线或电感制作成的高频扼流圈可以防止射频信号能量泄露以及避免射频信号对直流电源的影响。

图4 电调部分及馈电偏置部分ADS仿真图

3 微带梳状线可调滤波器的仿真设计

图5为两部分综合后的ADS仿真原理图。由此综合后，经过对二极管所加偏压的优化，得到最终在所选5个频点的仿真结果如图6(a)～图6(e)所示。

图5 梳状可调滤波器ADS原理图

各仿真结果所对应的二极管电压如表2所示。

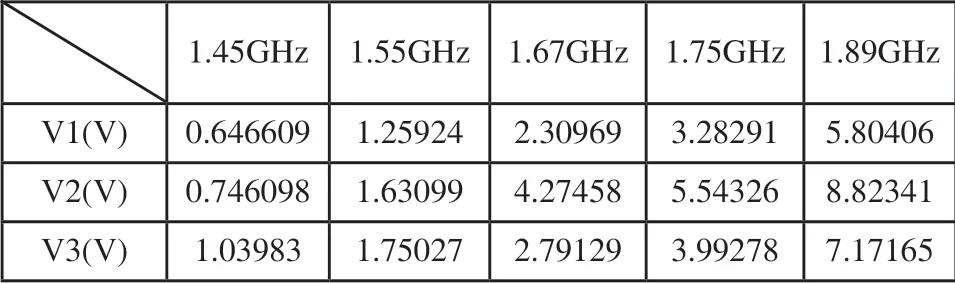
表2 各频点优化后二极管偏压值

图6 仿真结果2

图6 (a)～图6(e)所示的结果表明设计的梳状线带通滤波器的中心频率可以在1.45GHz～1.89GHz之间灵活调节，3dB带宽基本保持在100MHz。验证了利用变容二极管改进的梳状线带通滤波器可以实现在L波段上中心频率可调、带宽不变的设计方案。

由以上的仿真结果可以得出以下五点结论：

1）随着中心频率的提高，滤波器的带内插入损耗有所减小，这主要是由于变容管的Q值随频率增大而提高引起的。

2）滤波器的3dB带宽随中心频率的提高而略微变窄，主要是在滤波器的几何尺寸保持不变的情况下中心频率改变造成了耦合系数改变，从而3dB带宽受到影响。

3）电调滤波器的带内插损较大。造成这个问题的主要原因有三个：一是选用微带结构，这种结构的传输线Q值比悬置微带等传输线的小，损耗也大很多；二是串联电容及变容管的Q值不够高，使得滤波器的插入损耗较增大，并且串联电容及变容管存在一定容差，而选用3阶滤波器模型需要3个变容二极管，3个变容二极管之间的容差使得性能恶化；三是偏置滤波部分的串联电感不能完全隔断高频能量，造成高频能量从直流端有所泄漏。

4）平行微带线间的边缘场构成梳状谐振器间的耦合，故平行微带线之间的距离及宽度决定了耦合情况。变容二极管的电容值改变时，只改变谐振频率不改变耦合，这样使得驻波系数恶化。驻波比恶化程度与中心频率的调谐程度成正比，这制约着滤波器的动态范围。但是如果要进行实际测试，需固定滤波器的尺寸不变，故在中心频率远离可调范围中心频率时，仿真所得的回波损耗太大，不符合设计要求。

5）带外抑制基本符合设计要求。低频方向衰减平滑，而高频方向衰减比较陡峭。

4 结束语

文章主要研究了梳状线滤波器中心及带宽可调的原理设计。中心及带宽可调梳状滤波器的设计包括梳状线带通滤波器、电调部分和偏置滤波部分。文章首先介绍了中心及带宽可调滤波器的设计及滤波器的电调原理，然后给出了所选取的5个频点上梳状带通滤波器的仿真结果，最后给出了在1.45GHz～1.89GHz频段内可调谐的微带梳状电调滤波器的仿真结果，其中包括提出偏置滤波部分的解决方案。最后，对仿真结果进行了分析和讨论。

[1] I. C.Hunter,J. D.Rhodes. Electronically tunable microwave bandpass filter[J].IEEE Trans.Microw.Theory Tech.,1982, 30(9)：1354-1360.

[2] Vikram Sekar,Marcelino Armendariz,Kamran Entesari. A 1.2-1.6GHz Substrate-intergated-waveguide RF MEMS Tunable Filter[J].IEEE Trans. Microw. Theory Tech.,2011,59(4)：866-876.

[3] El-Tanani, M. A.,Rebeiz, G. M. Corrugated Microstrip Coupled Lines for Constant Absolute Bandwidth Tunable Filters[J].IEEE Trans. Microw.Theory Tech.,2010,58(4)：956-963.

[4] Ramesh Grag,I.J. Bahl.Characteristics of Coupled Microstrip lines[J].IEEE Trans. Microw. Theory Tech.,1979,27(7)：700-705.

[5] Chih-Chieh Cheng,Rebeiz,G.M..High-Q 4-6-GHz Suspended Stripline RF MEMS Tunable Filter With Bandwidth Control[J]. IEEE Trans. Microw. Theory Tech.,2011,59(10 Pt.1)：2469-2476.

[6] Yuan Chun Li, Quan Xue.Tunable Balanced Bandpass Filter With Constant Bandwidth and High Common-Mode Suppression[J]. IEEE Trans. Microw.Theory Tech.,2011,59(10 Pt.1)：2452-2460.

[7] Derek Scarbrough,Charles Goldsmith, John Papapolymerou, Yuan Li. Miniature Microwave RF MEMS Tunable Waveguide Filter[A].Proceedings of the 39th European Microwave Conference[C].2009：1860-1864.

[8] Peng Wen Wong,Ian C.Hunter.Electronically Reconfigurable Microwave Bandpass Filter[J].IEEE Trans.Microw.Theory Tech.,2009,57(12)：3070-3079.

[9] Moon-Seok Chung, Il-Soo Kim,Sang-Won Yun. Varactor-tuned hairpin bandpass filter with an attenuation pole[A].Asia-Pacific Microwave Conference Proceedings[C].2005.

[10] Jia-Sheng Hong.Reconfigurable Planar Filters[J].IEEE Microwave Magzine,2009,10(6)：73-83.

[11] Mohammed A.El-Tanani,Gabriel M. Rebeiz.A Two-pole Twozero Tunable Filter with Improved Linearity[J].IEEE Trans. Microw.Theory Tech.,2009,57(4)：830-839.

[12] Xiu Yin Zhang,Quan Xue. High-selectivity Tunable Bandpass Filters with Harmonic Suppression[J].IEEE Trans. Microw. Theory Tech.,2010,58(4)：964-969.

[13] Yong-Hoon Chun,Jia-Sheng Hong. Electronically Reconfigurable Dual-mode Microstrip Open-loop Resonator Filter[J].IEEE Microw.Wireless Compon.Lett.,2008,18(7)：449-451.

[14] George L. Matthaei, Leo Young,E.M.T.Jones.Microwave Filters, Impedance-Matching Networks, and Coupling Structures[M].Mc-Graw Hill,1964.

[15] Skyworks Solutions,Inc.SMV1405-SMV1413 Series：Silicon Abrupt Junction Varactors,Packaged and Bondable Chips[R].www.skyworksinc.com,2011.

[16] Skyworks Solutions,Inc.Varactor SPICE Models for RF VCO Applications[R].www.skyworksinc.com,2010.