具有非线性耦合的Lurie动态网络的函数投影同步

毛北行， 李巧利

(1.郑州航空工业管理学院 数理系， 郑州 450015； 2.河南工业大学 理学院， 郑州 450001)



具有非线性耦合的Lurie动态网络的函数投影同步

毛北行1*， 李巧利2

(1.郑州航空工业管理学院 数理系， 郑州 450015； 2.河南工业大学 理学院， 郑州 450001)

研究了Lurie混沌系统的函数投影同步问题，构造了两类Lurie非线性耦合的驱动响应动态网络模型，基于Lyapunov稳定性理论，说明了Lurie混沌系统在函数投影方法下是同步的，最后仿真例子，表明了方法的有效性．

Lurie混沌系统； 投影同步； 复杂网络

混沌同步一直是非线性科学领域的研究热点问题之一，自Pecora和Carroll于20世纪90年代提出混沌系统的完全同步方法以来，混沌同步研究取得了巨大的进展[1-5]，近年来，混沌同步的应用从物理学迅速扩展到自动化控制，复杂网络以及保密通信等领域. 1999年，R.Mainieri等通过对耦合部分线性系统的研究指出，耦合的主从系统状态下的输出不仅相位是锁定的，而且各对应状态的振幅还按某一比例关系演化，这类混沌同步现象称为投影同步. 文献[6]基于单向耦合原理研究了一类混沌系统的修正函数投影同步问题，并给出了两种响应系统的设计方案，由于只需要向响应系统传送一个驱动变量，因而实用性更强. 文献[7]研究了耦合混沌系统的自适应修正函数投影同步问题. 通过设计合适的控制器和自适应律实现了函数投影同步，所设计的控制策略对模型不确定和外扰有较好的鲁棒性. 文献[8]利用线性反馈控制和自适应控制两种方法，研究了时滞和非时滞耦合的驱动响应动态网络的函数投影同步问题. 上述文献研究的都是投影同步问题．

另一方面，Lurie系统中包含控制系统中的多种非线性环节，能够概括工程问题中的许多实际问题，因而Lurie系统的研究引起了国内外学者的广泛兴趣.文献[9]基于自适应控制方法研究了一类Lurie系统的混沌同步问题，通过求解一个黎卡提方程设计了全局渐近控制律. 文献[10]基于线性矩阵不等式处理方法，研究了Lurie系统的脉冲控制问题，该种方法所需的代价小，性能可靠. 文献[11]基于单向耦合原理研究了Lurie系统的修正函数投影同步问题.，给出了系统的设计方案，但讨论的不是复杂网络混沌系统. 而关于Lurie复杂网络混沌系统的研究结果还十分少见，本文研究了Lurie混沌系统的函数投影同步问题，构造了两类Lurie非线性耦合的驱动响应动态网络模型，基于Lyapunov稳定性理论，说明了Lurie混沌系统在函数投影方法下是同步的，最后仿真例子，表明了该方法的有效性.

1 主要结果

以下考虑Lurie混沌系统

(1)

其中，x(t)=[x1，x2，...，xn]T∈Rn是系统的状态向量，C为适当维数的常数矩阵.f(Cx(t))为非线性函数．

以(1)作为驱动系统，构造如下具有非线性耦合的响应系统动态网络为

(i=1，2，…，N)，

(2)

其中，yi(t)为网络第i个节点的状态向量，ui(t)为加在第i个节点上的控制器，aij表示响应网络的非线性耦合配置矩阵的矩阵元，反映了网络的拓扑结构和节点的耦合强度，满足aij≥0(i≠j)，同时对角线元素定义为

(3)

在现实世界中存在双向连接、单向链接的网络和单双混合连接的网络. 双向连接的网络是若第i个节点和第j个节点相连接，则第j个节点和第i个节点也相连接. 而单向连接的网络是若第i个节点和第j个节点相连接，则第j个节点和第i个节点不连接，例如万维网是单向连接.一般地，若不考虑节点间的耦合强度的不同，则认为双向连接的网络其耦合配置矩阵是对称的，而单向和单双向混合连接的网络的耦合配置矩阵是不对称的，为了使设计的模型更加具有代表性，所以本文对耦合配置矩阵(aij)的对称性不作要求.

当比例函数α(t)为常数时，称(1)与(2)实现投影同步，特别的，当α(t)=1时，称(1)与(2)完全同步，当α(t)=-1,称(1)与(2) 实现反同步．

引理1[12]任给x，y∈Rn以及正定矩阵S，有2xTy≤xTSy+yTS-1y.

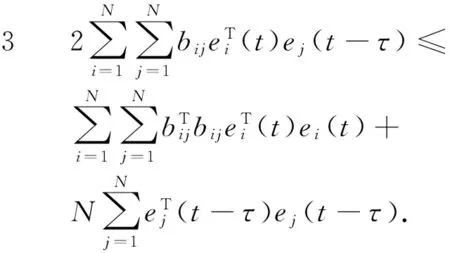
证明同引理2的证明，过程略．

(4)

证明定义同步误差ei(t)=yi(t)-α(t)x(t),则误差系统的导数为:

由引理1很容易得到

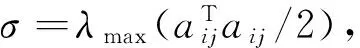
以下考虑Lurie混沌系统

(5)

其中,x(t)=[x1，x2，...，xn]T∈Rn是系统的状态向量，C为适当维数的常数矩阵.f(Cx(t))为非线性函数．

以(5)作为驱动系统，构造如下具有非线性耦合的响应系统动态网络

(6)

其中，yi(t)为网络第i个节点的状态向量，ui(t)为控制输入，aij，bij表示响应网络的非线性耦合配置矩阵的矩阵元，反映了网络的拓扑结构和节点的耦合强度，满足aij≥0(i≠j)，bij≥0(i≠j)同时对角线元素分别定义为

(7)

N(σ1+σ2+1)-K<0,

(8)

证明定义同步误差ei(t)=yi(t)-α(t)x(t),则误差系统的导数为

构造Lyapunov函数

则有

由引理2很容易得到

由引理3很容易得到

2 仿真算例

选取Lorenz系统做为驱动系统，系统描述为

其中,x1，x2，x3为状态变量，a，b，c为系统参数，当a=10，b=28，c=8/3时系统处于混沌状态. 为了方便，取含三个节点的网络进行仿真．

含有三个节点的非线性耦合的响应动态网络描述为

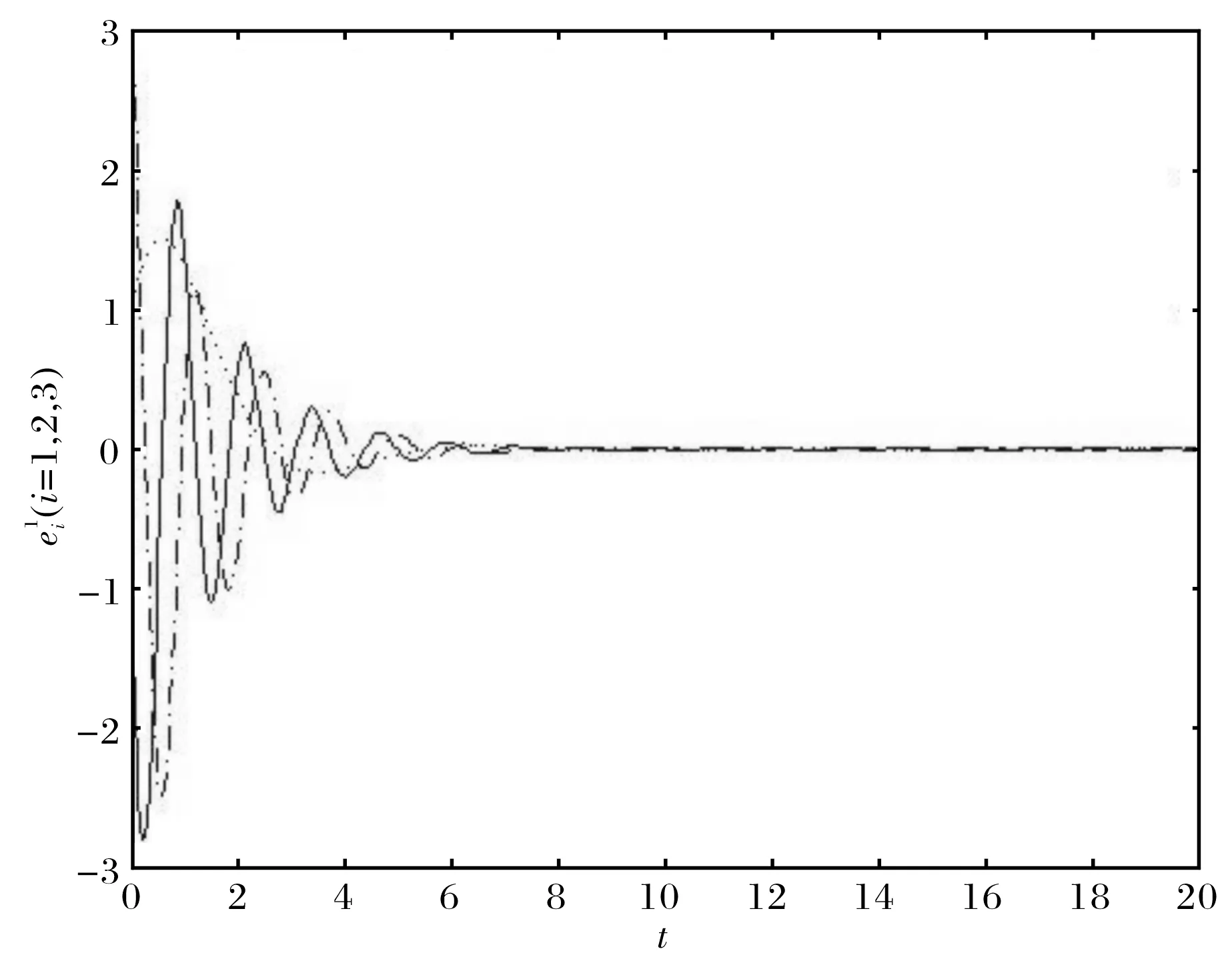
图1 定理1中系统的误差曲线

图2 定理2中系统的误差曲线

另一模型对应的系统为

3 结论

本文研究了Lurie混沌系统的函数投影同步问题，构造了两类Lurie非线性耦合的驱动响应动态网络模型，基于Lyapunov稳定性理论，说明了Lurie混沌系统在函数投影方法下是同步的，最后仿真例子，表明了方法的有效性. 本文采用比线性耦合功能更强的非线性耦合进行节点之间的相互连接构成完全网络， 该模型中驱动系统和网络节点的系统是任意的，不需要必须是部分线性系统，因此更具一般意义．

[1]PecoraLM，CarrollTL.Synchronizationinchaoticsystems[J].PhysRevLett， 1990， 64(8):821-824．

[2]PecoraLM，CarrollTL.Drivingsystemswithchaoticsignals[J].PhysRevA， 1991， 44(4):2374-2383．

[3]YooWJ，JiDH，WonSC.Synchronizationoftwodifferentnon-autonomouschaoticsystemsusingfuzzydisturbanceobserver[J].PhysicsLettersA， 2009， 374(11):1354-1361．

[4]FallahiK，LeungH.Achaossecurecommunicationschemebasedonmultiplicationmodulation[J].CommunicationsinNonlinearScienceandNumericalSimulation， 2010， 15(2):368-383．

[5] 吕 翎， 李 纲， 张 檬, 等. 全局耦合网络的参数辨识与时空混沌同步[J].物理学报， 2011， 60(9)：5051-5056．

[6] 李建芬， 李 农. 一类混沌系统的修正函数投影同步[J].物理学报， 2011， 60(8)：5071-5077．

[7] 方 洁， 胡智宏， 江 泳. 耦合混沌系统自适应修正函数投影同步[J].信息与控制， 2013， 42(1)：39-45．

[8] 李德奎， 张建刚. 时滞和非时滞耦合的驱动响应动态网络的函数投影同步[J].太原理工大学学报:自然科学版， 2013， 44(2)：162-168．

[9] 何汉林， 涂建军， 熊 萍. 一类Lurie混沌系统的全局渐近同步[J].华中科技大学学报:自然科学版， 2010， 38(2)：38-40．

[10] 毛北行， 王东晓， 卜春霞.Lurie混沌系统的脉冲控制同步[J].华中师范大学学报：自然科学版， 2012， 46(3)：297-299．

[11] 毛北行， 程春蕊， 卜春霞.Lurie混沌系统的修正函数投影同步[J].数学杂志， 2013， 33(4)：717-780．

[12] 卞秋香， 姚洪兴. 复杂网络的线性广义同步[J].系统工程理论与实践， 2011， 31(7)：1334-1340．

Function projective synchronization of Lurie dynamical networks with nonlinear coupling

MAO Beixing1， LI Qiaoli2

(1.Department of Mathematics and Physics， Zhengzhou Institute of Aeronautical Industry Management， Zhengzhou 450015;2.College of Science， Henan University of Technology， Zhengzhou 450001)

The problem of function projective synchronization of Lurie dynamical networks with nonlinear coupling is studied in the paper.Two drive-response dynamical model with nonlinear coupling is founded in the paper. It is proved that Lurie chaotic systems is synchronized using modified function projective synchronization approach based on Lyapunov stable theory .Numerical simulations example of chaotic system verify the effectiveness of the proposed method．

Lurie chaotic systems; projective synchronization; complex networks

2014-07-05.

国家自然科学基金项目(51072184)；国家自然科学基金数学天元基金项目(11226337)；航空基金项目(2013ZD55006)；河南省高等学校青年骨干教师资助计划项目(2013GGJS-142)；郑州航空工业管理学院青年基金项目(2012113004)；河南省教育厅科学技术重点项目(14A110027).

1000-1190(2015)01-0047-05

TP273+.2

A

*E-mail: bxmao329@163.com.