分子动力学研究抑制剂APV与HIV-1蛋白酶的作用机制

时术华， 张少龙， 张庆刚

( 1. 山东建筑大学理学院, 济南 250101; 2. 山东师范大学物理与电子科学学院, 济南 250014)

分子动力学研究抑制剂APV与HIV-1蛋白酶的作用机制

时术华1， 张少龙2， 张庆刚2

( 1. 山东建筑大学理学院, 济南 250101; 2. 山东师范大学物理与电子科学学院, 济南 250014)

采用分子动力学模拟和结合自由能计算研究了抑制剂APV与HIV-1蛋白酶的作用机制. 研究结果表明范德瓦尔斯作用主控了APV与HIV-1蛋白酶的结合. 采用基于残基的自由能分解方法计算了抑制剂-残基相互作用，结果表明9个残基Gly27、Ile32、Val47、Ile50、Ile84、Ala28′、Gly49′、Ile50′和Arg87′与APV产生了大于1.0 kcal/mol的强相互作用，而且证明CH-π，CH-O相互作用和极性作用是其结合的主要形式. 期待该结果可以为以HIV-1蛋白酶为靶标的抗艾滋病药物设计提供理论上的指导.

分子动力学； 结合自由能； HIV-1蛋白酶； MM-PBSA

1 引 言

获得性免疫缺陷综合症简称艾滋病, 是威胁人类生命健康的重大疾病之一. 近年来，死于艾滋病的人数呈逐年递增趋势, 共计2500多万感染者死亡. 在艾滋病的生命周期中, HIV-1蛋白酶(PR)起着关键作用, 它能将gag和gag-pol表达的多聚蛋白分裂装配为成熟并具有感染性的病毒颗粒[1, 2]，因此阻断和抑制PR的活性功能是临床上治疗艾滋病的一条有效途径.

PR由两条相同的肽链组成, 每一条肽链均包含99个氨基酸, 结构上呈C2对称性. PR的活性中心由保守残基序列Asp-Thr-Gly构成, 并且其催化位点位于两个亚基的接触面[3, 4]. 两个天冬氨酸Asp25和Asp25′在催化过程中起重要作用[5].

PR抑制剂已成为艾滋病联合用药治疗方案的重要组成部分. 美国食品药物管理局已颁布9种PR抑制剂, 其中多数药物是以PR切割HIV前体蛋白上的活性位点为模板设计的[6]. 抑制剂Amprenaavir(APV)对PR有较强的抑制效果，其抑制常数为0.04-4.9 nM[7, 8]. 本文将从原子层次上识别APV与PR的作用机制，这对于以PR为靶标的用于治疗艾滋病的高效抑制剂的研发具有重要意义.

近年来, 随着计算理论的快速发展和计算机模拟技术的迅速提高, 分子动力学模拟和结合自由能计算成为研究抑制剂-蛋白质相互作用的重要工具[9-13]. MM-PBSA是一种基于经验方程来快速计算抑制剂与蛋白质结合自由能的有效方法[14, 15]，该方法已经成功用于研究抑制剂-蛋白质和蛋白质-蛋白质相互作用[16-18]. 目前尚未发现APV与PR作用机制的分子动力学模拟和结合自由能计算研究，因此本文将采用MM-PBSA方法计算APV与PR的结合自由能, 研究控制APV与PR结合的主体力量，同时采用基于残基的自由能分解方法计算抑制剂-残基相互作用[19], 这些计算有利于从原子层次上阐明APV与PR复合体的结构亲和能关系. 研究结果能为以PR为靶标的抗艾滋病药物设计提供一定的理论启示.

2 研究方法

取自蛋白质库的晶体结构(3S45)用于动力学模拟的初始构象. APV与蛋白酶结合体中的结晶水分子保留在初始构象中，由Amber 12中的leap模块添加晶体结构中缺失的氢原子[20]，蛋白质和结晶水的力场参数由Amber 12中的ff03力场产生[21]. 考虑天冬氨酸的质子化, 对残基Asp25的氧原子O2执行了质子化. APV的力场参数源自GAFF力场[22]，使用Amber 12中的半经验量子力学计算(AM1)给APV分配了BCC原子电荷，APV-PR结合体溶解在显性的TIP3P的水盒子里，水盒子边缘与复合体最近原子的距离是10.0Å. 四个氯离子添加到由水和复合体组成的系统中来保证模拟系统呈现电中性.

采用Amber12中的sander模块对整个体系执行两步系统优化来消除一些原子间不合理的接触：(1) 约束溶质、优化溶剂和中和离子. 约束力常数设为50 kcal/(mol·Å2); (2) 无约束地优化整个系统. 在每一步优化中，首先执行2500步的最陡下降优化，接着执行2500步的共轭梯度优化；然后在500 ps内把系统从0 K加热到300 K，随后进行500 ps的常温300 K、常压1标准大气压条件下的动力学平衡；最后是15 ns无约束的分子动力学模拟. 模拟期间采用SHAKE方法限制所有与氢原子有关的化学键的伸缩[23]，模拟积分步长设为2 fs；采用PME方法用来计算长程的静电相互作用；采用周期性边界条件消除溶剂盒子的边缘效应，非成键相互作用的截断值为10.0 Å.

2.2 MM-PBSA方法计算结合自由能

采用单轨迹方案的MM-PBSA方法计算APV与PR的结合自由能，按照一定的时间间隔从动力学模拟平衡轨迹中抽取200个构象用于结合自由能分析，构象中删掉水分子和氯离子，计算结合自由能的方程可表示为：

ΔG=ΔEMM+ΔGsol-TΔS

(1)

式中ΔEMM是气相中的分子力学能，ΔGsol表示溶解自由能对APV结合的贡献，TΔS表示熵变对结合自由能的贡献. ΔEMM可进一步分解为：

ΔEMM=ΔEele+ΔEvdw

(2)

其中ΔEele和ΔEvdw分别表示气相中的静电相互作用能和范德瓦尔斯相互作用能. 溶解自由能ΔGsol可表示为：

ΔGsol=ΔGpb+ΔGsurf

(3)

其中ΔGpb和ΔGsurf分别表示极性溶解自由能和非极性溶解自由能，前者可使用Amber 12中的PBSA方法求解泊松-玻尔兹曼方程获得，溶质和溶剂的电介常数分别设为1.0和80.0，ΔGsurf由如下经验方程计算：

ΔGsurf=γSASA+β

(4)

式中γ和β值分别取为0.00542 kcal/(mol·Å2)和0.92 kcal/mol.TΔS是由于抑制剂与蛋白酶结合前后自由度变化诱导的熵变对结合自由能的贡献，通过使用简振模分析和传统的热力学计算获得.

2.2 分组患者HEART、MEWS评分比较 急诊住院者HEART评分及MEWS评分均显著高于留院观察者（P＜0.05）；30 d死亡患者 HEART和 MEWS评分分值均较急诊住院患者有进一步增高，且两者分别与存活者比较，差异有统计学意义（P＜0.05）。见表1。

3 结果与讨论

3.1 分子动力学的平衡

本文对APV-PR复合物系统执行了15 ns的分子动力学模拟. 为了评估动力学平衡的稳定性，使用Amber 12中的Ptraj程序计算了PR主链原子相对于晶体结构的均方根偏差(Root-mean-square deviation, RMSD)和蛋白结构的回旋半径随时间的变化关系(图2A和B). 由图2A观察到，PR主链原子的RMSD大约在模拟开始4.5 ns后达到平衡. 结合体平衡后RMSD的平均值为1.22 Å，其涨落范围小于0.49 Å，该结果表明PR与APV组成的系统的动力学平衡是可靠的.

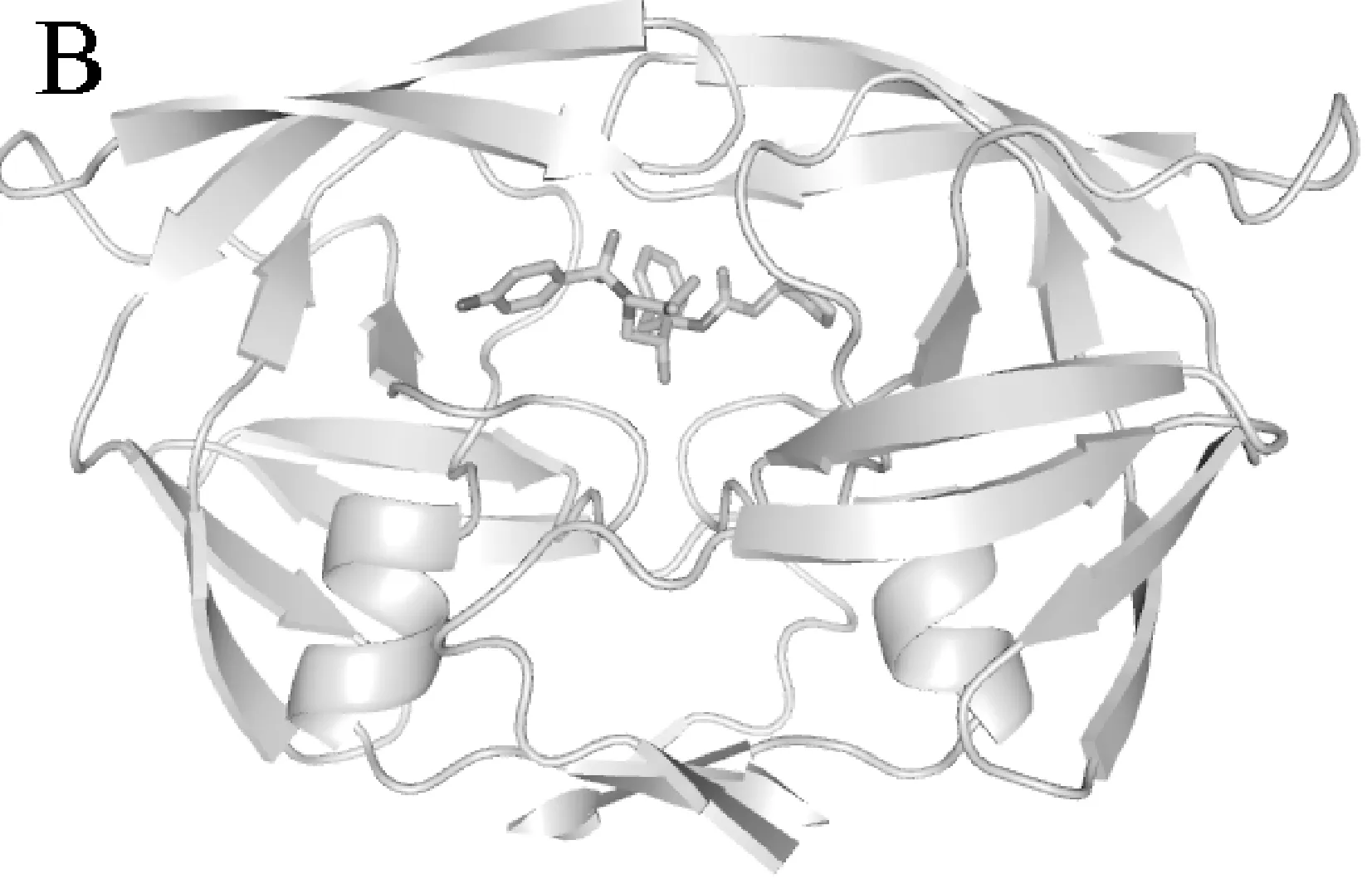
图1 分子结构：(A)抑制剂APV的结构；(B)APV与PR复合物的结构Fig.1 Structures of molecule: (A) the structure of APV; (B) the structure of the complex APV-PR

为了从整体结构上评估动力学模拟的稳定性，蛋白酶的回旋半径随模拟时间的涨落由图2B给出.由图2B观察到，在动力学模拟开始大约4 ns后，整体结构的涨落趋向稳定，未出现异常情况. 该结果说明动力学模拟过程中，蛋白酶的结构是稳定的. 以上的RMSD和回旋半径分析表明用于后续分析计算的动力学模拟轨迹的稳定性是可靠的.

3.2 结合自由能计算

本文采用MM-PBSA方法计算了APV与PR的结合自由能，并分析APV与蛋白酶作用的主体力量. 表1中列出了计算得到的结合自由能以及其贡献成分.

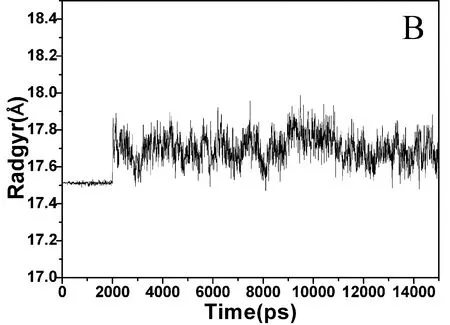
图2 (A) MD模拟中PR主链原子的RMSD；(B) MD模拟中PR结构的回旋半径Fig.2 (A) RMSD of backbone atoms in PR during molecular dynamics simulation; (B) Gyroradius of PR during molecular dynamics

表1表明抑制剂APV与PR的结合自由能是-8.4 kcal/mol，这表明APV能够与PR产生较强的相互作用. 由表1看到，抑制剂与蛋白酶产生的范德瓦尔斯作用能(ΔEvdw)是-66.1 kcal/mol，这表明范德瓦尔斯作用能有效地促进抑制剂与蛋白酶的结合. ΔGsurf与溶剂可及表面积相对应的非极性相互作用能, 其值为-7.0 kcal/mol, 该作用也能够为APV与蛋白酶的结合也提供有利贡献. 表1的结果表明抑制剂APV与PR的静电相互作用能(ΔEele)为-40.6 kcal/mol，也有利于抑制剂与PR的结合，但完全被另一个大小为大小为57.37 kcal/mol极性溶解自由能(ΔGpb)抵消.

依据表1，熵变对结合自由能的贡献(-TΔS)为24.35 kcal/mol，该成分消弱了抑制剂与蛋白酶的结合. 在有利的两个相互作用成分中(ΔEvdw和ΔGsurf)，范德瓦尔斯相互作用能是非极性相互作用能的9倍之多. 从上面的分析可以得出结论，范德瓦尔斯相互作用是控制抑制剂APV与PR的结合的主要力量. 上述分析与几个其他几个工作组有关PR的研究结果相吻合.

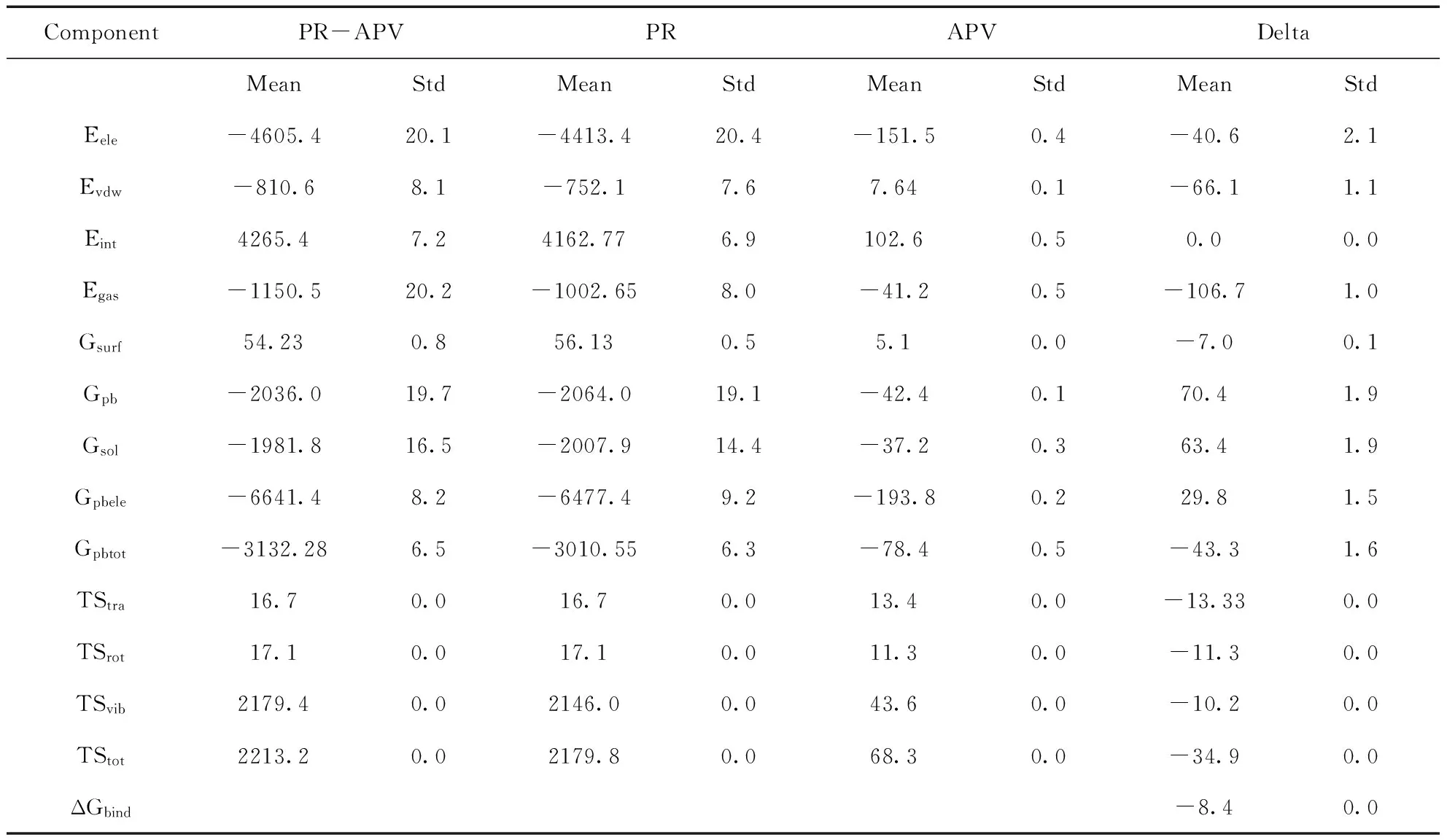
表1 MM-PBSA计算所得到的能量(kcal/mol)a

aEele和Evdw分别表示静电作用能和范德瓦尔斯作用能，Eint表示由键伸、键角弯折和二面角扭转贡献的内能，Egas= Eele+ Evdw+ Eint; Gsurf和Gpb分别是非极性溶剂化能和极性溶剂化能，Gsol是溶解自由能且Gsol= Gsurf+ Gpb；Gpbele= Eele+ Gpb; Gpbtot= Gsol+ Egas; TStra, TSrot和TSvib分别表示体系的平动、转动和振动自由度熵变对自由能的贡献；TStot= TStra+ TSrot+TSvib; ΔGbind= Gpbtot- TStot

3.3 结构-亲和能关系

为了能从原子层次上更好地理解抑制剂APV与蛋白酶的作用机制，进而阐明它们的结合模式，本文采用基于残基的自由能分解方法计算了抑制剂与蛋白酶残基的相互作用能(图3)，同时在图4中显示了PR的关键残基与抑制剂APV的相对空间位置. 由图3可以看出9个残基Gly27、Ile32、Val47、Ile50、Ile84、Ala28′、Gly49′、Ile50′和Arg87′与抑制剂APV产生了大于1.0 kcal/mol的强相互作用. 这9个残基为蛋白酶-抑制剂的结合提供了重要贡献, 结构亲和能关系分析如下.

图3 抑制剂APV与PR各个分离残基的相互作用谱Fig. 3 Inhibitor-residue interaction spectrum between the inhibitor APV and PR

从图3可以观察到，残基Ala28′与APV产生了最强的相互作用，该作用能量是-2.76 kcal/mol. 其作用的主要来源是Ala28′的烷基与APV右端芳香环之间的CH-π相互作用. 在结构上，Ile50的烷基与抑制剂APV右端的芳香环相邻近，产生较强的疏水性的CH-π相互作用；同时，Ile50的氮原子与APV的氧原子之间形成一个氢键(图4), 这两个相互作用为APV与蛋白酶的结合提供了-1.72 kcal/mol的贡献. Ile50′与APV的相互作用为-2.03 kcal/mol，这个作用主要由Ile50′的烷基与抑制剂APV左端的芳香环形成的CH-π作用相提供. 依据图4，残基Ile32、Ile47和Ile84的烷基与抑制剂左端的芳香环临近而产生CH-π作用，这三个作用分别为APV与蛋白酶的相互作用提供了-1.12、-1.12和-1.95 kcal/mol的能量贡献. 在结构上，残基Gly27和Gly49′的羰基氧原子与APV中间的苯环临近，形成了有利于抑制剂结合的CH-O相互作用，这两个相互作用分别为抑制剂结合贡献了-1.20和-1.52 kcal/mol作用能. Arg87′与抑制剂APV产生较强的相互作用(-1.19 kcal/mol)，该相互作用主要源自Arg87′的电荷与APV的羰基产生的极性相互作用. 上述分析基本上吻合了几个其他课题组的工作[24-26].

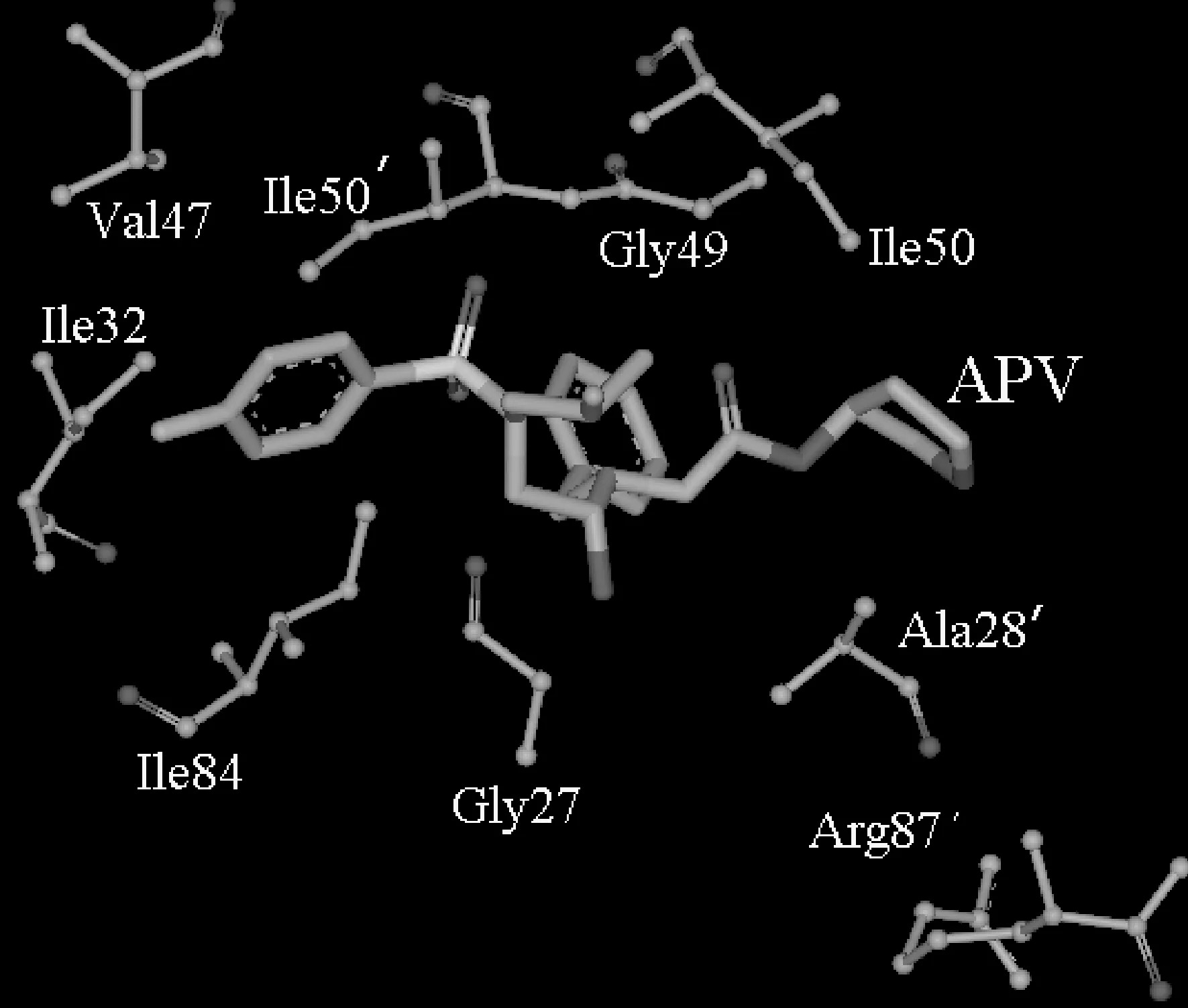
图4 PR和抑制剂APV复合体中主要残基的相对位置Fig. 4 Relative geometries of the key residues in PR-APV complex

4 结 语

本文对APV和PR的复合体系执行了15 ns的分子动力学模拟和结合自由能计算，研究了APV与PR的结合模式. 结果证明分子间的范德瓦尔斯作用主要驱动了抑制剂APV与PR的结合. 采用基于残基的自由能分解方法计算了APV与蛋白酶各残基的相互作用，结果表明9个残基Gly27、Ile32、Val47、Ile50、Ile84、Ala28′、Gly49′、Ile50′和Arg87′与APV产生较强相互作用, 结构亲和能关系分析证明CH-π，CH-O相互作用和极性作用驱动了APV与PR的结合. 该研究能为以PR为靶标的治疗艾滋病的药物设计提供重要理论启示.

[1] Judd D A, Nettles J H, Nevins N,etal. Polyoxometalate HIV-1 protease inhibitors. A new mode of protease inhibition [J].J.Am.Chem.Soc., 2001, 123: 886.

[2] Tie Y, Wang Y F, Boross P I,etal. Critical differences in HIV‐1 and HIV‐2 protease specificity for clinical inhibitors [J].ProteinScience, 2012, 21: 339.

[3] Blum A, Böttcher J, Heine A,etal. Structure-guided design of C 2-symmetric HIV-1 protease inhibitors based on a pyrrolidine scaffold? [J].J.Med.Chem., 2008, 51: 2078.

[4] Brik A, Wong C H. HIV-1 protease: mechanism and drug discovery [J].Org.Biomol.Chem., 2003, 1: 5.

[5] Perryman A L, Lin J H, McCammon J A. HIV‐1 protease molecular dynamics of a wild‐type and of the V82F/I84V mutant: Possible contributions to drug resistance and a potential new target site for drugs [J].ProteinScience, 2009, 13: 1108.

[6] Soriano V, Gomes P, Heneine W,etal. Human immunodeficiency virus type 2 (HIV‐2) in Portugal: Clinical spectrum, circulating subtypes, virus isolation, and plasma viral load [J].J.Med.Virol., 2000, 61: 111.

[7] Shen C H, Wang Y F, Kovalevsky A Y,etal. Amprenavir complexes with HIV‐1 protease and its drug‐resistant mutants altering hydrophobic clusters [J].FEBS.J., 2010, 277: 3699.

[8] Tie Y, Wang Y F, Boross P I,etal. Critical differences in HIV‐1 and HIV‐2 protease specificity for clinical inhibitors [J].ProteinScience, 2012, 21: 339.

[9] Chen J, Wang J, Zhu W,etal. A computational analysis of binding modes and conformation changes of MDM2 induced by p53 and inhibitor bindings [J].J.Comput.AidedMol.Des., 2013, 27: 965.

[10] Wu E L, Han K L, Zhang J Z H. Selectivity of neutral/weakly basic P1 group inhibitors of thrombin and trypsin by a molecular dynamics study [J].Chemistry- AEuropeanJournal, 2008, 14: 8704.

[11] Hu G D, Zhang S L, Liu X G,etal. Molecular dynamics and free energy calculation study progesterone binding to human progesterone receptor-ligand binding domain [J].J.At.Mol.Phys., 2010, 27: 333(in Chinese)[扈国栋, 张少龙, 刘新国, 等. 分子动力学模拟和自由能计算研究孕酮和孕酮蛋白受体的结合模式 [J]. 原子与分子物理学报, 2010, 27: 333]

[12] Cheng W Y, Liang Z Q, Zhang Q G,etal. Insight into p53-MDM2 interaction based on molecular dynamics simulation and molecular mechanics [J].J.At.Mol.Phys., 2012, 29: 393(in Chinese)[程伟渊, 梁志强, 张庆刚, 等. p53-MDM2 相互作用的分子力学和动力学研究 [J]. 原子分子物理学报, 2012, 29: 393]

[13] Chen J, Wang J, Xu B,etal. Insight into mechanism of small molecule inhibitors of the MDM2-p53 interaction: molecular dynamics simulation and free energy analysis [J].J.Mol.Graph.Model., 2011, 30: 46.

[14] Wang J, Morin P, Wang W,etal. Use of MM-PBSA in reproducing the binding free energies to HIV-1 RT of TIBO derivatives and predicting the binding mode to HIV-1 RT of efavirenz by docking and MM-PBSA [J].J.Am.Chem.Soc., 2001, 123: 5221.

[15] Wang W, Kollman P A. Free energy calculations on dimer stability of the HIV protease using molecular dynamics and a continuum solvent model1 [J].J.Mol.Biol., 2000, 303: 567.

[16] Yi C, Chen J, Zhu T,etal. Protonation of Asp25 of HIV-1 protease stabilizes its binding to the inhibitor GRL02031 [J].J.At.Mol.Phys., 2011, 28: 11(in Chinese)[伊长虹, 陈建中, 朱通, 等. Asp25质子化有利于HIV-1蛋白酶与抑制剂GRL02031结合 [J]. 原子分子物理学报, 2011, 28: 11]

[17] Chen J, Zhang D, Zhang Y,etal. Computational studies of difference in binding modes of peptide and non-peptide inhibitors to MDM2/MDMX based on molecular dynamics simulations [J].Int.J.Mol.Sci., 2012, 13: 2176.

[18] Shi S H, Chen J Z, Hu G D,etal. Molecular insight into the interaction mechanisms of inhibitors BEC and BEG with HIV-1 protease by using MM-PBSA method and molecular dynamics simulation [J].J.Mol.Struct.:THEOCHEM, 2009, 913: 22.

[19] Gohlke H, Kiel C, Case D A. Insights into protein-protein binding by binding free energy calculation and free energy decomposition for the Ras-Raf and Ras-RalGDS complexes [J].J.Mol.Biol., 2003, 330: 891.

[20] Case D A, Darden T A, Cheatham III T E,etal. AMBER 12[J].SanFrancisco:UniversityofCalifornia, 2012.

[21] Duan Y, Wu C, Chowdhury S,etal. A point-charge force field for molecular mechanics simulations of proteins based on condensed-phase quantum mechanical calculations [J].J.Comp.Chem., 2003, 24: 1999.

[22] Wang J, Wolf R M, Caldwell J W,etal. Development and testing of a general amber force field [J].J.Comput.Chem., 2004, 25: 1157.

[23] Coleman T G, Mesick H C, Darby R L. Numerical integration [J].Ann.Biomed.Eng., 1977, 5: 322.

[24] Böttcher J, Blum A, Heine A,etal. Structural and kinetic analysis of pyrrolidine-based inhibitors of the drug-resistant Ile84Val mutant of HIV-1 protease [J].J.Mol.Biol., 2008, 383: 347.

[25] Chen J, Zhang S, Liu X,etal. Insights into drug resistance of mutations D30N and I50V to HIV-1 protease inhibitor TMC-114: Free energy calculation and molecular dynamic simulation [J].J.Mol.Model., 2010, 16: 459.

[26] Hou T, Yu R. Molecular dynamics and free energy studies on the wild-type and double mutant HIV-1 protease complexed with amprenavir and two amprenavir-related inhibitors: mechanism for binding and drug resistance [J].J.Med.Chem., 2007, 50: 1177.

Molecular dynamics insights into binding mode of inhibitor APV to HIV-1 protease

SHI Shu-Hua1, ZHANG Shao-Long2, ZHANG Qing-Gang2

(1. School of Science, Shandong Jianzhu University, Jinan 250101, China；2.College of Physics and Electronics, Shandong Normal University, Jinan 250014, China)

Molecular dynamics simulation and binding free energy calculation was performed to study the binding mode of inhibitor APV to HIV-1 protease. The results show that van der walls energy is the main force driving the binding of APV to HIV-1 protease. Residue-based free energy decomposition was adopted to calculate the inhibitor-residue interaction and the results suggest that nine residues Gly27, Ile32, Val47, Ile50, Ile84, Ala28′, Gly49′, Ile50′ and Arg87′ in HIV-1 protease produce strong interactions with APV, at the same time, these results also show that the CH-π， CH-O and polar interaction are the main ones between APV and HIV-1 protease. We expect that this study can provide significant contributions to the designs of anti-AIDS targeting HIV-1 protease.

Molecular dynamics; Binding free energy; HIV-1 protease; MM-PBSA

2014-02-11

国家自然科学基金(11274206); 山东省自然科学基金(ZR2011HM048,ZR2013AM014); 山东建筑大学博士启动基金(XNBS1268)

时术华(1967—)，女, 山东文登人, 博士, 副教授, 主要研究领域为生物大分子的理论计算.E-mail: sdsfhf@sdjzu.edu.cn

103969/j.issn.1000-0364.2015.10.028

Q641.12

A

1000-0364(2015)05-0885-06