高振动激发K2与CO2间弱碰撞和强碰撞的分支比

2015-03-23王淑英阿拜艾力哈孜沈异凡

原子与分子物理学报 2015年5期

关键词：角动量弹性分子

王淑英，阿拜·艾力哈孜, 2，戴康，沈异凡

(1.新疆大学物理科学与技术学院，乌鲁木齐 830046; 2. 西安交通大学理学院，西安 710049)

高振动激发K2与CO2间弱碰撞和强碰撞的分支比

王淑英1，阿拜·艾力哈孜1, 2，戴康1，沈异凡1

(1.新疆大学物理科学与技术学院，乌鲁木齐 830046; 2. 西安交通大学理学院，西安 710049)

碰撞能量转移；弱碰撞和强碰撞；受激发射泵浦；速率系数；角动量改变； K2(v″)+CO2

1 引言

从分子碰撞实验中得到的能量转移分布函数表明了弱碰撞远多于强碰撞的发生，这里的“弱”和“强”指在碰撞中能量转移量的相对大小.因为弱碰撞仅引起分子小的能量和量子态的改变，在实验上区分分子的初态和终态较困难.举一个例子，某分子的高振动态与CO2碰撞，强碰撞使CO2(0000)高转动态得到布居，因为在碰撞前，按Boltzmann分布，在高转动态上基本无布居，故测得的布居全是由碰撞产生的[1,2].对于低位转动态，碰撞前就有布居，碰撞后该态的布居是保留不变，转移来和转移出去的代数和区分这三部分布居是这类实验的难点.

Mullin等[3-5]利用高分辨率瞬时红外吸收，研究了高振动激发吡嗪(C4H4N2)分别与DCl和CO2之间的能量转移，测量了初生转动态DCl(v=0,J=2-21)和CO2(0000,J=2-78)以及它们的平移能轮廓，得到了全部量子态分辨转动分布.CO2转动态分布呈双指数结构，其中77%属近弹性碰撞，23%为非弹性碰撞.高振动态能量增加16%，J态的平移能增加50%.转动分布对碰撞能量是敏感的，但弹性与非弹性碰撞的分支比是相同的.碰撞能量对能量转移速率系数影响较小，但与能量增益分布函数P(ΔE)有很大关系.

本实验利用受激发射泵浦激发K2基电子态的高位振动态v″=40,53，K2(v″)与CO2碰撞，利用瞬时泛频LIF测量，研究不同碰撞能量对CO2转动态分布，弱碰撞与强碰撞分支比以及对能量转移概率分布的影响.

2 实验方法

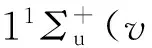
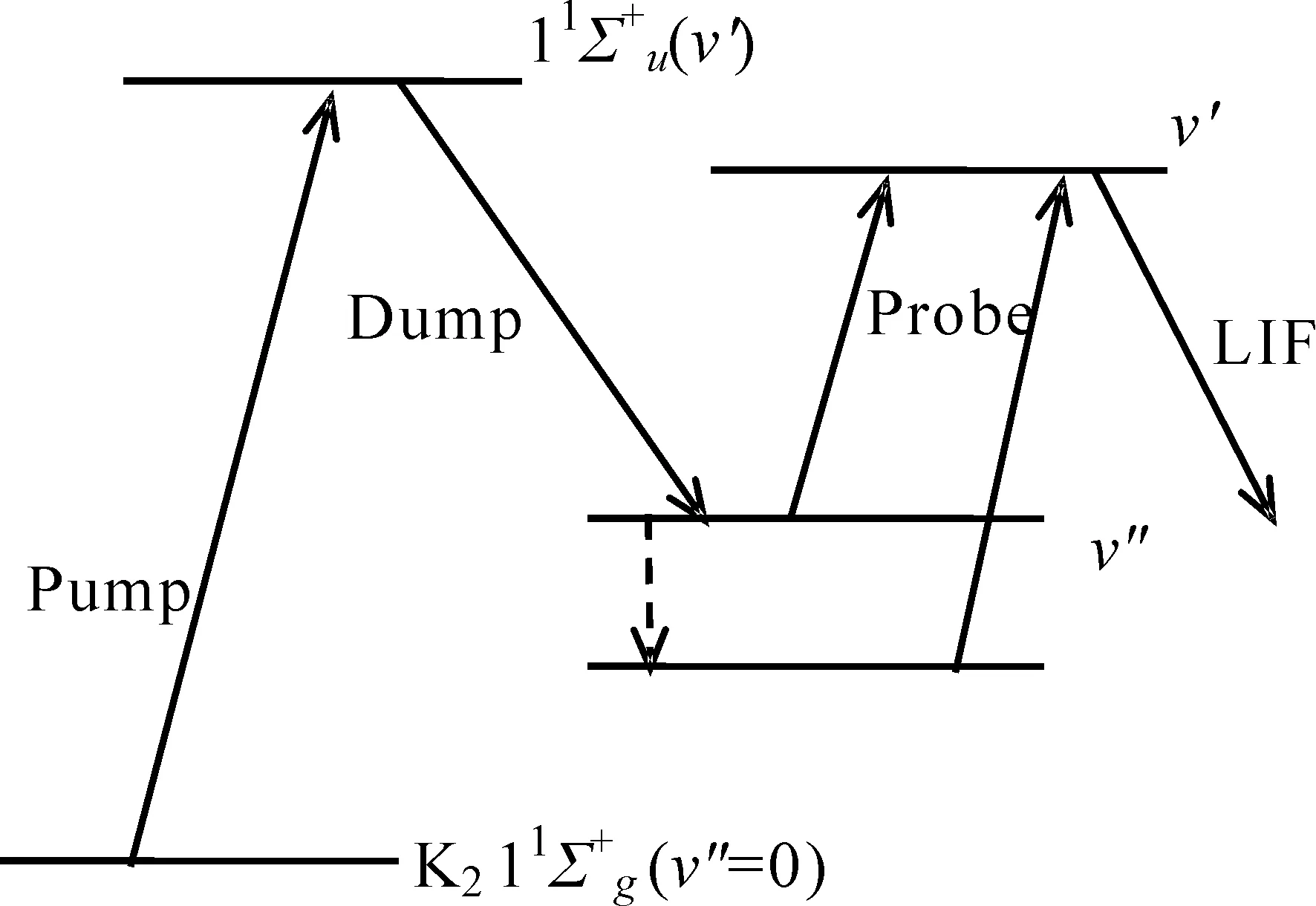
图1 受激发射泵浦能级图Fig.1 Energy diagram for Pump-Dump and Probe scheme

高激发K2(v″)与CO2强碰撞，使CO2的高转动态出现(appearence)布居，而对于K2(v″)与CO2的弱碰撞，则可使CO2低位转动态出现或部分倒空(depletion)布居.转动能级上原生态的布居由高分辨率瞬时泛频(1005,J+1)-(0000,J)LIF强度测量[6]，泛频波长约为790 nm[7].利用光纤将收集到的泛频荧光传送到门光子计数器.与OPO激光反向平行通过样品池的Ti宝石激光既作为高位K2(v″)态的检测光，也作为原生态CO2(0000,J)态的泛频检测光.荧光记录时间为1μs.

延迟脉冲发生器(DG535)使OPO延迟染料激光20ns，以避免二色多光子激发的产生.在本实验条件下，K2(v″)与CO2碰撞间隔平均约为4 μs[1]，门光子计数器延迟OPO1 μs，以满足一次碰撞条件.

一个5臂交叉热管炉作为样品池，4条臂平面交叉，与4臂垂直的第5小臂中存放金属K.在样品池的真空度达到10-4Pa时充入CO2，CO2的气压为2 Pa.用电热器加热样品池，样品池温度控制在450-850 K之间，由置于样品池中的热电偶测量.

滤光片把Ti宝石激光减至约0.1 μW.用光学吸收法[8]测量不同池温时K2高振动态的分子密度.本实验条件下，K2(v″=40,53)的分子密度在1010-1011cm-3之间.

3 结果与讨论

3.1 弱，强碰撞分支比

(1)

[CO2(J)]t=0由Boltzmann分布确定

[CO2(J)]t=0=[CO2]0(B/kT)

(2J+1)exp[-BJ(J+1)/kT]

(2)

上式中B=0.394cm-1是CO2的转动常数，[CO2]0为CO2密度，本实验中为5.2×1014cm-3，T为池温，从而由(1)式得到J态密度.

图2为池温600 K时K2(v″=40)与CO2碰撞后CO2(0000,J)的初生态分布，NJ为J态密度.该分布可用二个独立的指数函数拟合[5].

NJ=(2J+1)[I1exp(-EJ/kT1)+

I2exp(-EJ/kT2)]

(3)

其中EJ为转动能，T1和T2是二个不同的转动温度，I1和I2为相对强度.由图2的实验数据，对于K2(v″=40)+CO2，得到T1=581±70 K的低能分布和T2=1395±167 K的高能分布.对于K2(v″=53)+CO2，作类似分析，得到T1=621±76 K和T2=1556±187 K.因此低J态主要发生近弹性的弱碰撞，高J态则发生非弹性的强碰撞.

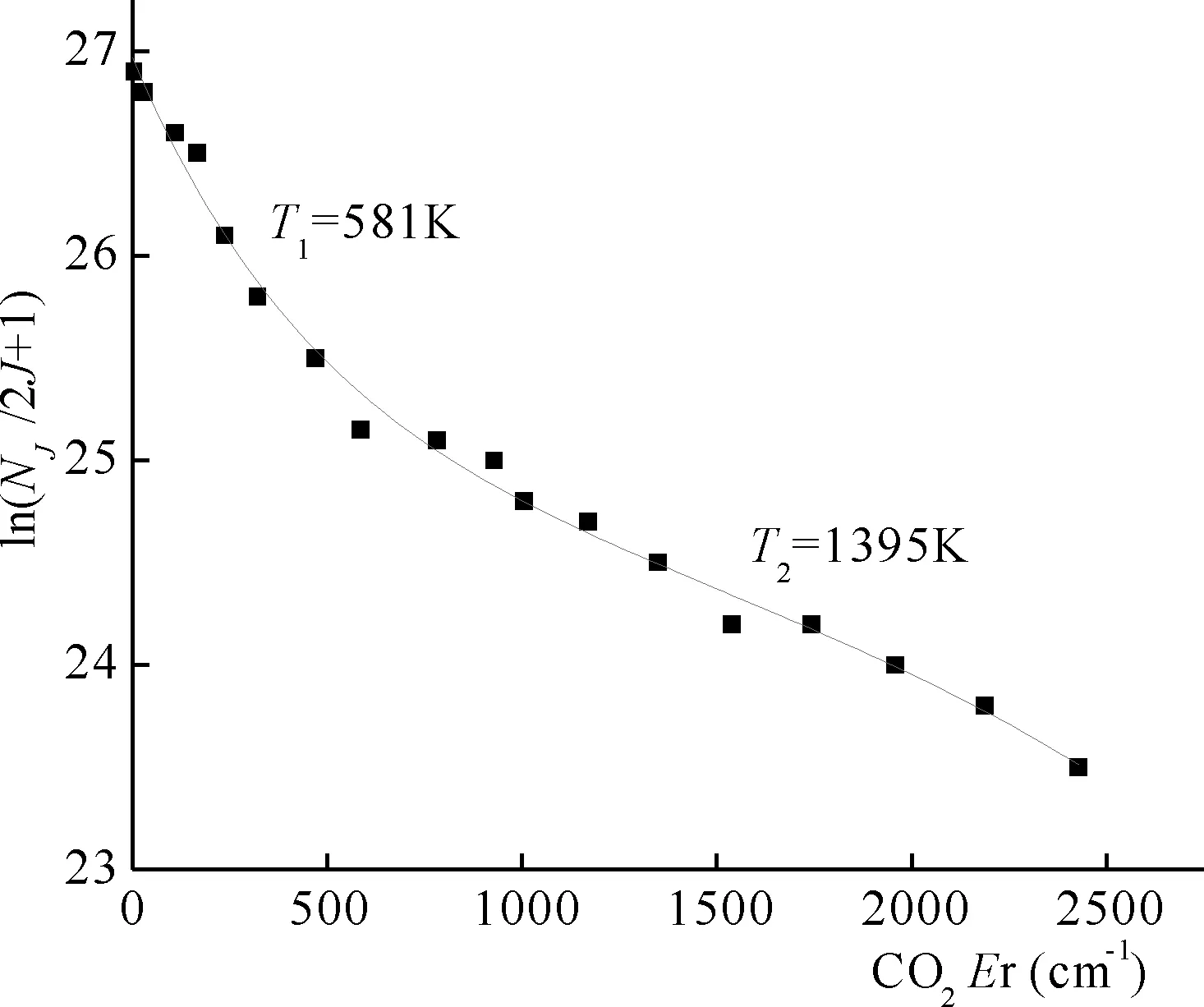
图2 CO2(0000)与K2(v″=40)碰撞后的初生态半对数描述Fig. 2 Semilog plot of the nascent rotational distribution of scattered CO2(0000) from collisions with K2(v″=40) showing the existence of a bimodal product state distribution

图3(a)为K2(v″=40,53)二个高位振动态分别与CO2弱碰撞后CO2转动分布的比较，(b)为强碰撞后转动分布的比较，随K2(v″)能量的增加，弱碰撞和强碰撞的能量转移都增加了(布居分布向高转动能转移)，但弱，强碰撞产生的布居分支比对K2(v″)能量不敏感，均约为5:1.

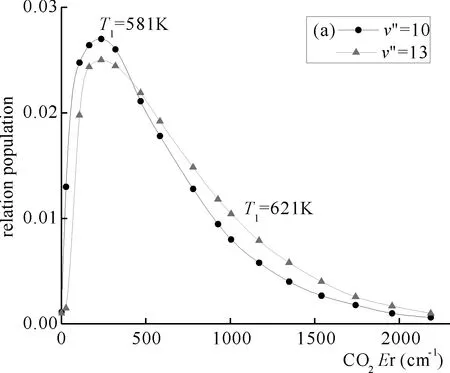
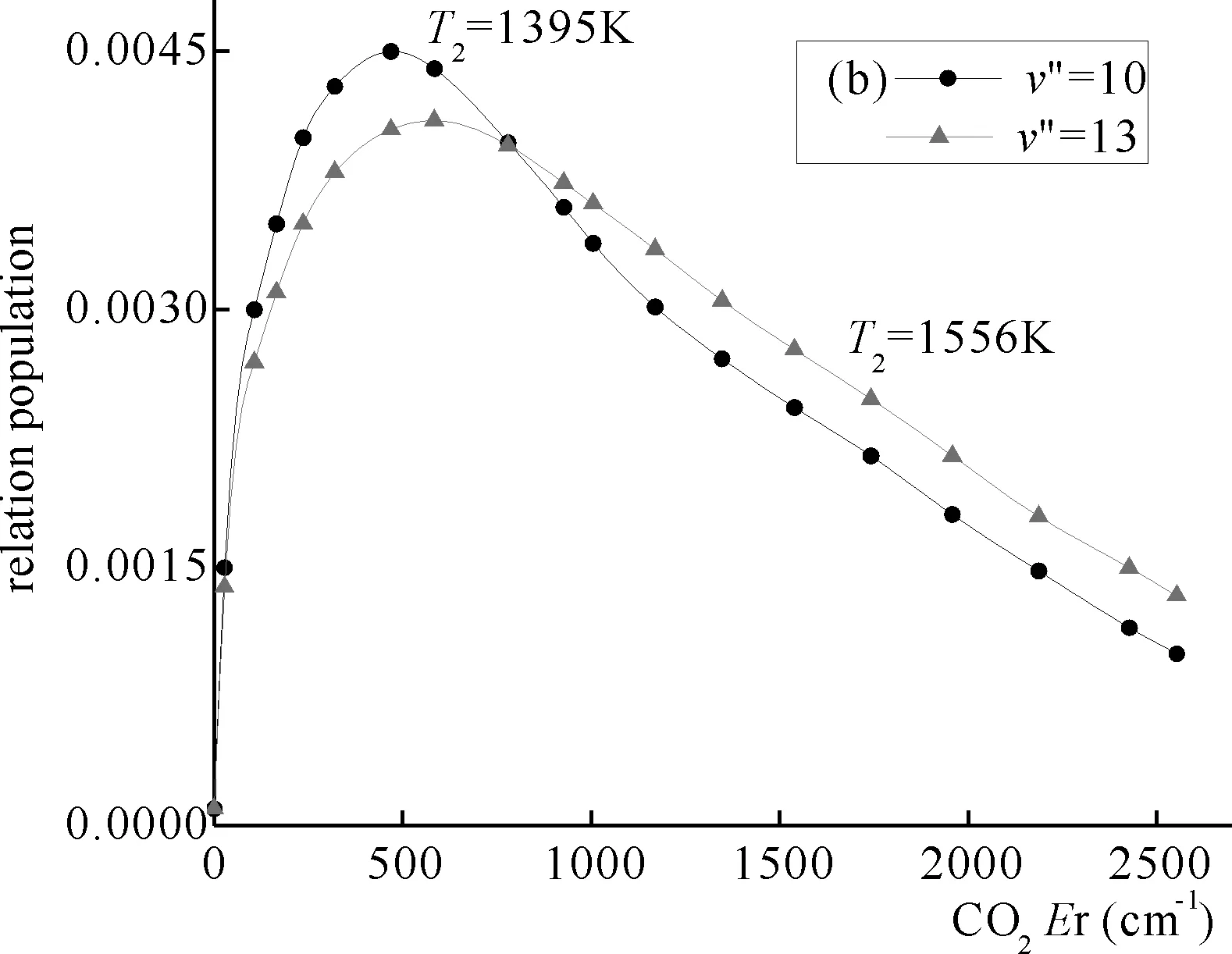
图3 弱碰撞(a)与强碰撞(b)转动分布的比较Fig. 3 Comparison of the (a) weak and (b) strong collision rotational distributions

3.2 能量转移速率系数测量

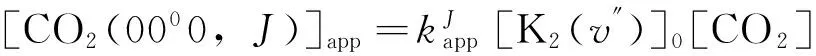
(4)

[K2(v″)]0是未发生碰撞时K2(v″)的密度.因碰撞而倒空(deplete)J态布居的速率系数为kdep

Δ[CO2(0000,J)]dep=

-kdepz(J)[K2(v″)]0[CO2]Δt

(5)

z(J)为J态分子在全部CO2分子中的占比，由Boltzmann分布决定，Δt取1μs.从(4)和(5)式得到

(6)

上式中，z(J)-1=[CO2]/[CO2(J)]=(B/kT(2J+1)exp[-BJ(J+1)/kT])-1，T为池温.(Δ[CO2(J)]app+Δ[CO2(J)]dep)/[CO2(J)]是在碰撞1μs后J态布居的相对变化，可用瞬时泛频LIF强度的相对变化表示，故(6)可改写为

(7)

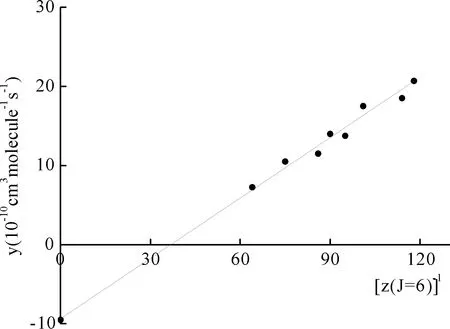
图4 K2(v″=40)与CO2碰撞时和kdep的导出Fig. 4 ″=40) and CO2 collisions

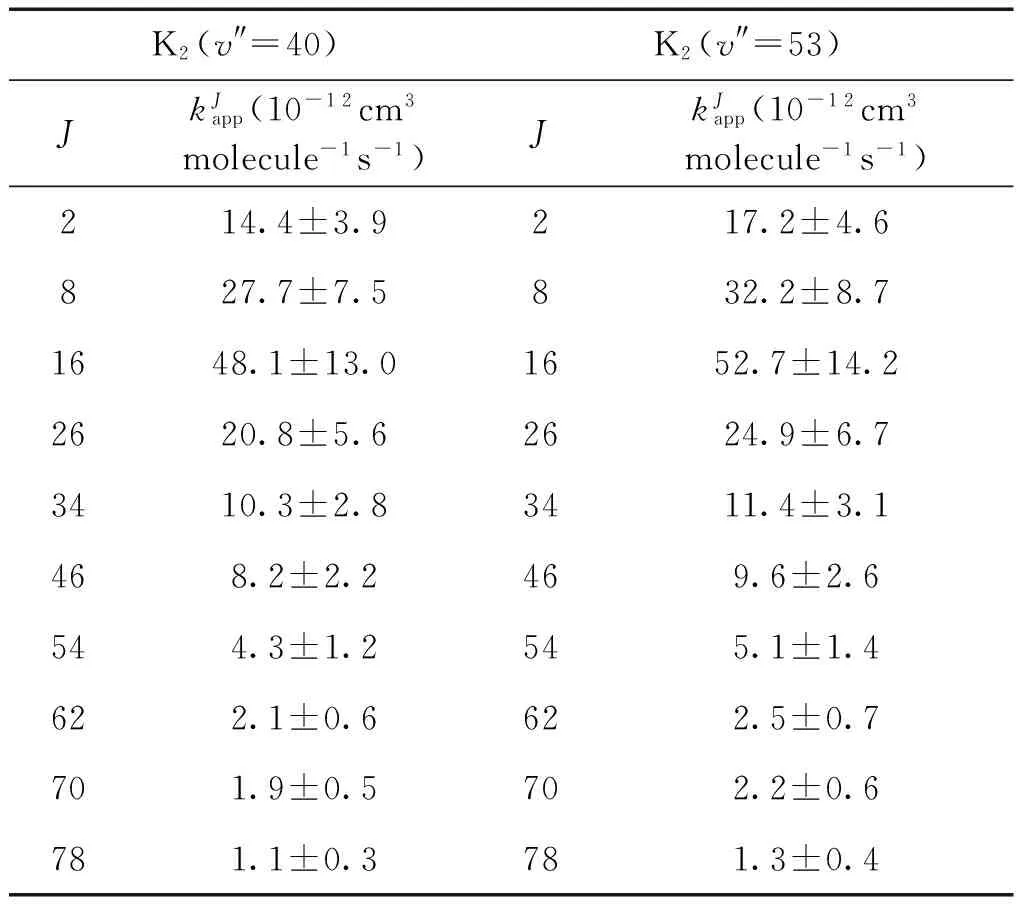
K2(v″=40)K2(v″=53)JkJapp(10-12cm3molecule-1s-1)JkJapp(10-12cm3molecule-1s-1)214.4±3.9217.2±4.6827.7±7.5832.2±8.71648.1±13.01652.7±14.22620.8±5.62624.9±6.73410.3±2.83411.4±3.1468.2±2.2469.6±2.6544.3±1.2545.1±1.4622.1±0.6622.5±0.7701.9±0.5702.2±0.6781.1±0.3781.3±0.4

3.3 振动-转动，平动(V-RT)能量转移中的角动量改变

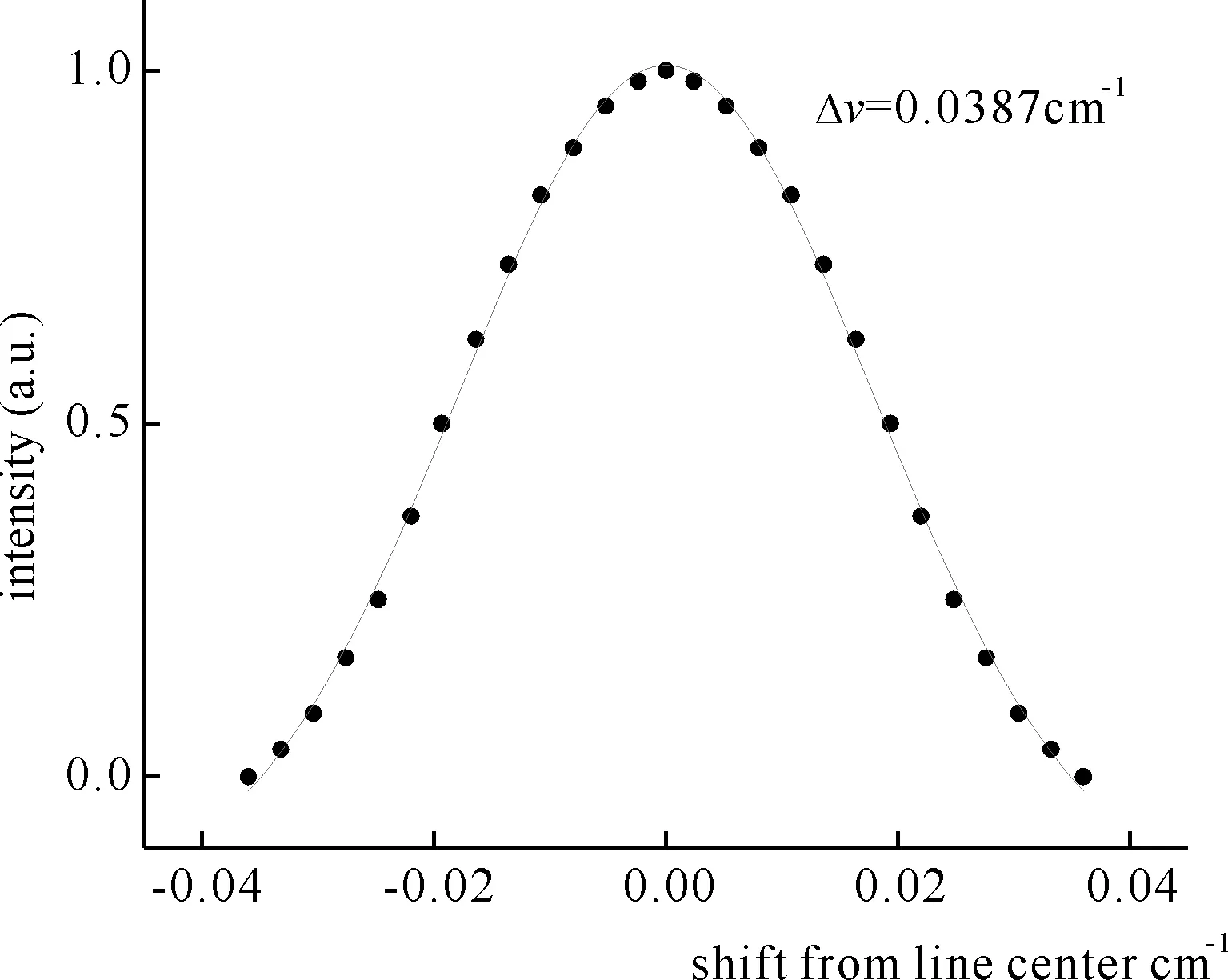
图5 CO2 P48泛频跃迁线的Doppler轮廓Fig. 5 Doppler broadened overtone transition line profile for CO2 P48 collected at t=1 μs following excitation of K2(v″=40) (T=600 K)

表2 CO2(0000,J=44-78)各态的角动量改变和反冲速度

Table 2 Angular momentum changes and recoil velocities for various states of CO2(0000,J=44-78) through collisions with K2(v″=53) (T=600 K)

J<ΔJ>Tapp(K)(ms-1)(ms-1)<Δvrel>(ms-1)4433.9760±80654±421020±112406±454839.0782±82664±431036±114422±465243.8826±87761±491187±131573±635446.2851±89784±501223±135609±676053.1878±92809±561262±139648±716457.5895±94825±571287±142673±746659.8915±96843±581315±145701±776862.0967±102891±611390±153776±857266.31025±108945±651474±162860±957872.81129±1191041±711624±1791010±111

图6描绘了<Δvrel>作为<ΔJ>的函数的变化情况，<Δvrel>随<ΔJ>的增加而单调增大，且随<ΔJ>增大，<Δvrel>加速增大，这与McCaffery等[10-12]的碰撞能量转移的角动量模型的结论是一致的.对于v″=40和53，<Δvrel>的趋向是相似的，而v″=53有较大的<Δvrel>.K2能量以3069 cm-1增加到3828 cm-1，能量增加25%，而反冲速度增加约47%.

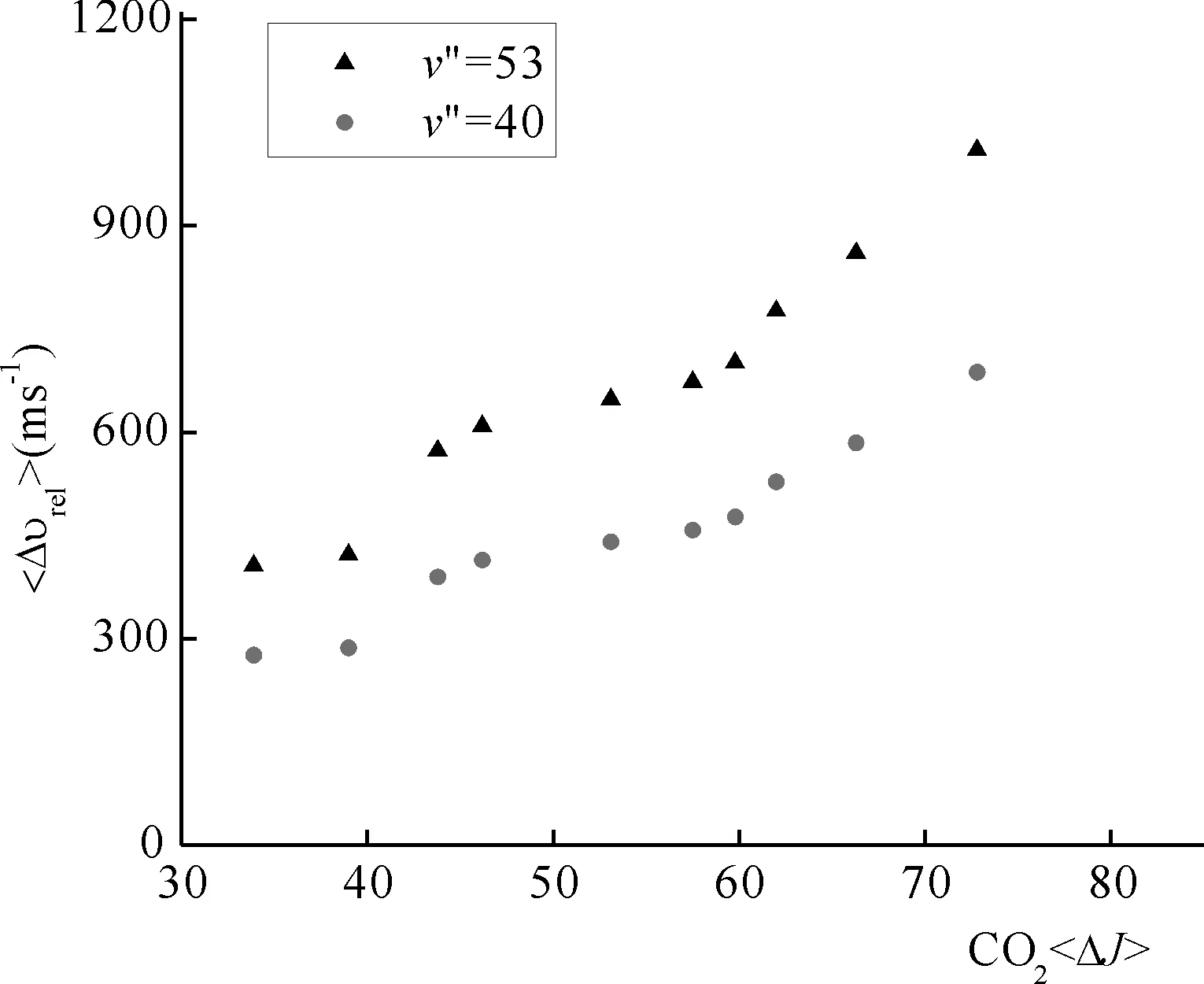
图6 角动量平均变化与反冲速度平均变化的关系 Fig. 6 Correlation between the average change in angular momentum of CO2 and the average change of recoil velocity <Δvrel> from K2(v″)/CO2 collisions

3.4 能量转移概率分布函数

在K2(v″)与CO2碰撞中，利用转动线的Doppler增宽和能量转移速率系数，由文献[13,5]的方法得到的能量转移概率分布函数PJ(ΔE)，用来表示CO2中各转动态的能量分布，完全的能量转移分布函数P(ΔE)是所有PJ(ΔE)之和.图7给出了v″=40和53两个不同能量的P(ΔE)曲线.

图7 P(ΔE)与K2(v″)能量关系Fig. 7 K2(v″) energy-dependence of the energy transfer probability distribution function P(ΔE) for K2(v″)/CO2 collisions

由二参量单指数衰变模型[14]

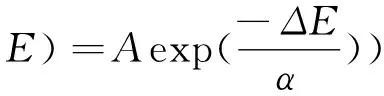
(8)

式中α表示K2(v″)的能量损失-<ΔE>down，A为归一化常数.拟合实验数据得到-<ΔE>down=293 cm-1(对v″=40)和-<ΔE>down=450 cm-1(对v″=53)，可以看到P(ΔE)对高振动态能量变化是敏感的.

4 结论

实验研究了高振动K2(v″=40,53)与CO2碰撞后CO2J态分布，量子态分辨测量表明了V-RT轨道是主要的能量转移途径.由双指数转动分布得到约有83%的碰撞属弱碰撞，而17%属非弹性强碰撞.对于强碰撞，CO2J态的角动量和反冲速度都有大的增加.随K2能量的增加，能量转移分布P(ΔE)迅速增宽.

[1] Yuan L, Du J, Mullin A S. Energy-dependent dynamics of large-DeltaE collisions: highly vibrationally excited azulene (E=20390 and 38580 cm-1) with CO2[J].J.Chem.Phys., 2008, 129(1): 014303.

[2] Johnson J A, Duffin A M, Hom B J,etal. Quenching of highly vibrationally excited pyrimidine by collisions with CO4[J].J.Chem.Phys., 2008, 128: 054304.

[3] Du J, Yuan L, Hsieh S,etal. Dynamics of weak and strong collisions: Highly vibrationally excited pyrazine (E=37900 cm-1) with DCl[J].J.Phys.Chem. A, 2008, 112(39): 9396.

[4] Havey D K, Du J, Liu Q,etal. Full state-resolved energy gain profiles of CO2(J=2-80) from collisions of highly vibrationally excited molecules. 1. Relaxation of pyrazine (E=37900 cm-1)[J].J.Phys.Chem. A, 2010, 114(3): 1569.

[5] Du J, Sassin N A, Havey D K,etal. Full state-resolved energy gain profiles of CO2from collisions with highly vibrationally excited molecules. II. energy-dependent pyrazine (E=32700 and 37900 cm-1) relaxation [J].J.Phys.Chem. A, 2013, 117(46): 12104.

[6] Zhu Y L, Zhong C Y, Yolwas A,etal. Energy dependence of collision transfer of CO2with highly vibrationally excited RbH(X1Σ+,v"≥15) [J].J.At.Mol.Phys., 2012, 29(6): 1035(in Chinese) [朱永乐，仲崇玉，阿布都艾尼·由力瓦斯，等. 高位振动态RbH(X1Σ+, v"≥15)与CO2碰撞转移中的能量相关性 [J]. 原子与分子物理学报, 2012, 29(6): 1035]

[7] Lu Y, Liu A W, Pan H,etal. High sensitivity cavity ring down spectroscopy of13C16O2overtone bands near 806nm [J].JQSRT, 2012, 113: 2197.

[8] Cui X H, Mu B X, Shen Y F,etal. Vibrational relaxation and vibration-rotation energy transfer between highly vibrationally excited KH (X1Σ+,v=14-21) and CO2[J].JQSRT, 2012, 113: 2081.

[9] McCaffery A J, Osborne M A, Marsh R J,etal. The role of angular momentum in collision-induced vibration-rotation relaxation in polyatomics [J].J.Chem.Phys., 2004, 121: 169.

[10] McCaffery A J, Alwahabi Z T, Osborne M A,etal. Rotational transfer, an angular momentum model [J].J.Chem.Phys., 1993, 98: 4586.

[11] Marsh R J, McCaffery A J. Quantitative prediction of collision-induced vibration-rotation distributions from physical data [J].J.Phys. B, 2003, 36: 1363.

[12] McCaffery A J, Marsh R J. Modeling disequilibrium in gas ensembles: How quantum state populations evolve under multicollision conditions; CO*+Ar, CO, O2, and N2[J].J.Chem.Phys., 2010, 132: 074304.

[13] Michaels C A, Flynn G W. Connecting quantum state resolved scattering data directly to chemical kinetics: Energy transfer distribution functions for the collisional relaxation of highly vibrationally excited molecules from state resolved probes of the bath [J].J.Chem.Phys., 1997, 106: 3558.

[14] Miller L A, Barker J R. Collisional deactivation of highly vibrationally excited pyrazine [J].J.Chem.Phys., 1996, 105: 1383.

Branching ratios of weak and strong collisions:highly vibrationally excited K2(v″) with CO2

WANG Shu-Ying1, ABAI Alghazi1, 2, DAI Kang1, SHEN Yi-Fan1

(1. School of Physics Science and Technology, Xinjiang University, Urumqi 830046, China;2.School of Sciences, Xi′an Jiaotong University, Xi′an 710049, China)