形变碳纳米管中水的输运行为研究
2015-03-23余幼胜张泓筠尹海峰曾凡菊
余幼胜, 岳 莉, 张泓筠, 尹海峰, 曾凡菊, 张 颂
(凯里学院物理与电子工程学院, 凯里 556011)
形变碳纳米管中水的输运行为研究
余幼胜, 岳 莉, 张泓筠, 尹海峰, 曾凡菊, 张 颂
(凯里学院物理与电子工程学院, 凯里 556011)
水分子通过碳纳米管的运输行为对认识生命的新陈代谢活动、海水淡化和纳米运输器件有着重要的参考作用. 本文通过分子动力学的方法研究了水分子通过形变碳纳米管的运输行为, 即椭圆柱状碳纳米管的离心率e对管内水分子输运的影响. 结果发现椭圆柱状碳纳米管的离心率对管内水分子的偶极矩概率分布、径向函数分布和流量有重要的影响作用. 分析认为碳纳米管的形变使管内水分子的偶极矩态及其运输状态发生变化; 同时也发现在一定范围内通过改变碳纳米管的形状能起到分子开关的作用.
碳纳米管; 水分子; 运输行为; 形变
1 引 言
水是生命之源, 也是维持生命的重要物质. 对生物体而言, 体内水的运输对生物的很多活动有着重要的作用, 在这些活动中都涉及到水通道蛋白. 由于碳纳米管具有简单、稳定的结构, 故有学者[1]利用它作为水通道蛋白的简化模型来研究水的运输行为, 结果表明管内水分子具有特殊的运输行为. 2001年Hummer等人[2]利用分子动力学的方法研究了水在(6,6)型碳纳米管内的运输行为, 结果发现碳纳米管内水分子运输时形成一维水分子链. 目前, 国内外的研究主要集中在两方面, 一是通过对碳纳米管进行修饰的方法探究水分子的运输行为, 如李敬源等人[3]将电荷置于碳纳米管之外, 探究电荷与碳纳米管间的距离对管内水分子的影响, 发现水分子运输和电荷与碳纳米管间的距离有着紧密的联系; 周毅等人[4]同样通过电荷外置的方法研究了电荷的大小对水分子流量的影响. 另一是通过改变碳纳米管结构的方法来认识水分子运输, 如王俊等人[5]利用分子动力学的方法系统的研究了管径和手性矢量对管内水分子的静态和动态行为; W. D. Nicholl等人[6]利用分子动力学的方法研究了碳纳米管的长度对管内水分子的流量的影响; L. B. da Silva[7]和袁虹君等人[8]分别研究了不同直径的扶手型碳纳米管对管内水分子结构和运输特性的影响. 徐葵[9]通过分子动力学模拟的方法探究了形变碳纳米管的管径对管内流体的影响. S. Wang等人[10]通过模拟的方法研究了弯曲碳纳米管的弯曲度对管内水分子的运输的影响, 而何俊霞等人[11]通过改变形变位置探究纳米通道中的窄结构对水输运产生的开关特性.
由于生产合成中出现椭圆柱状的形变碳纳米管,而椭圆柱状碳纳米管对管内水分子运输的影响未见到相关报道. 因此本文通过分子动力学的方法主要探究椭圆柱状碳纳米管的离心率e对水分子运输的流量、偶极矩分布和径向分布函数的关系. 本文的研究对认识生命体系新陈代谢、海水淡化、纳米运输器件的研发有着重要的物理意义.
2 模型与方法
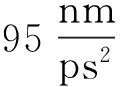

图1 模型结构示意图, 其中(a)图阴影部分为control region, 图(b)为不同离心率的碳纳米管横截面示意图Fig. 1 The sketches of model structure,where the control region is indicated by shading in (a), and (b) is the sketch of cross-section of carbon nanotubes on different ellipse ratio
3 结果与讨论
3.1 形变碳纳米管内水分子偶极矩概率分布
为了研究水分子在碳纳米管内的取向, 图2给出了碳纳米管内水分子偶极矩方向与碳纳米管z轴正方向之间夹角的概率分布. 设偶极矩方向与z轴正方向的夹角小于90°时为正偶极矩态, 其大于90°为负偶极矩态. 由图2可以发现: 当(6,6)和(7,7)型碳纳米管为圆柱状(e=1)时, 水分子偶极矩概率分布曲线均只存在一个峰, 且峰对应的位置为48°, 这说明水分子通过圆柱状碳纳米管时为正偶极矩态, 无负偶极矩态的出现. 由图(a)可以发现: 当手性矢量(6,6)碳纳米管的离心率e≤1.0和e=2.0时其管内水分子偶极矩的概率分布相同, 而离心率e=1.5和e=1.8的概率分布相同, 但它们都只存在一个峰且峰的位置和圆柱状碳纳米管峰的位置相同, 这表明在这些情况下碳纳米管内水分子均为正偶极矩态; 但是对于e=1.2的(6,6)型碳纳米管而言, 其偶极矩概率分布存在两个峰, 分别位于48°和132°, 并且位于48°的偶极矩概率小于位于132°的, 这说明水分子处于负偶极矩态强于处于正偶极矩态. 分析认为随着碳纳米管的离心率的增加, 大多数水分子由正偶极矩态转化为负偶极矩态: 当离心率再增加时, 负偶极矩态又转化为正偶极矩态. 由图(b)可以发现: 当(7,7)型碳纳米管的离心率在0.8
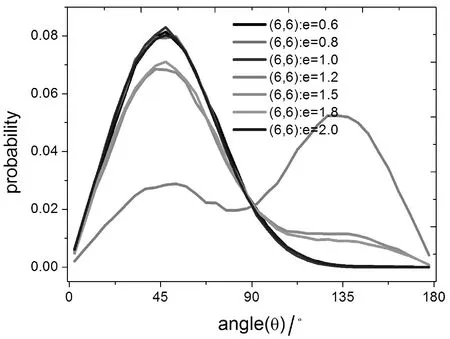
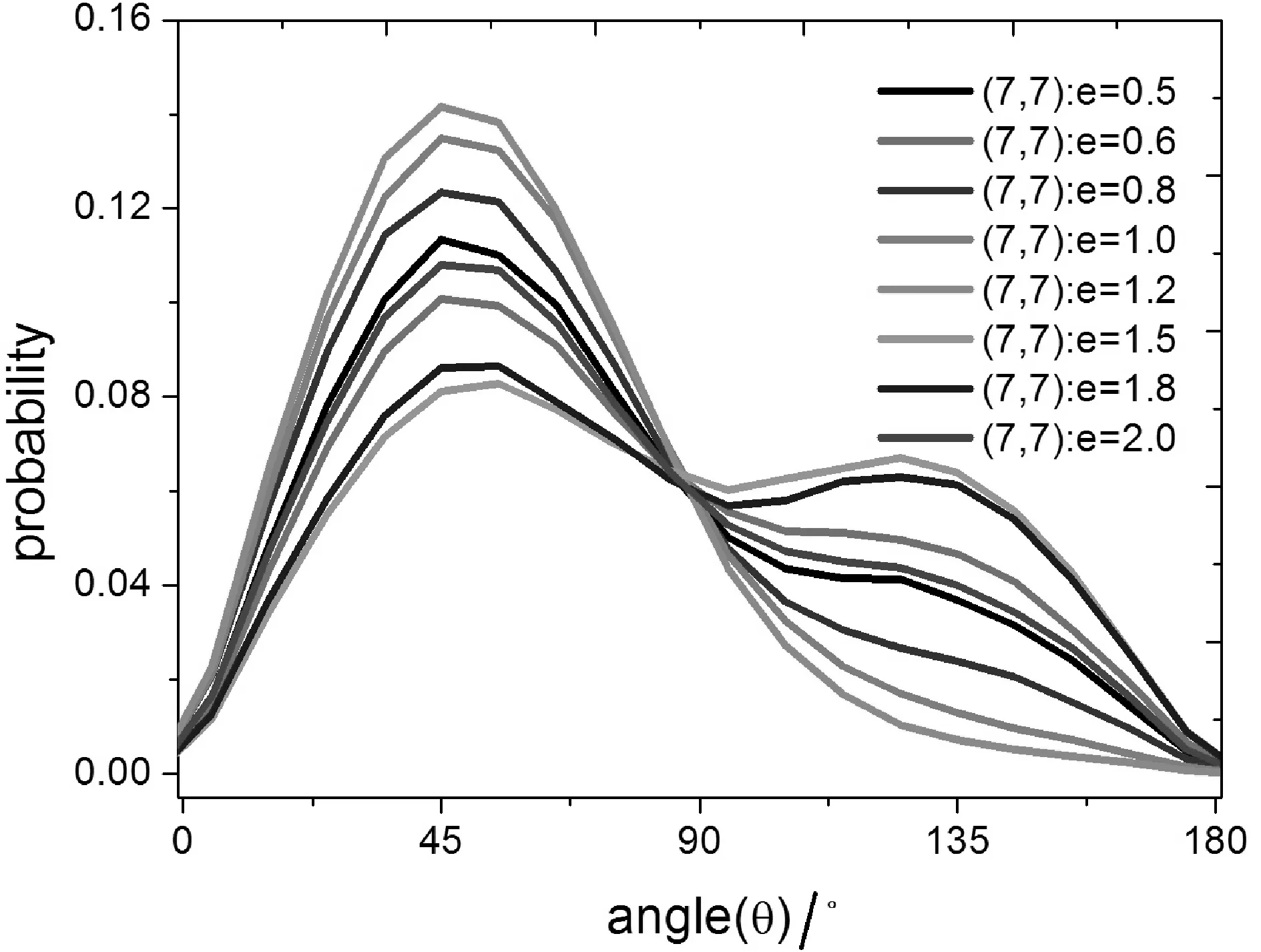
图2 水分子在碳纳米管内的偶极矩概率分布, 其中图(a,b)分别为(6,6)和(7,7)型碳纳米管Fig. 2 The probability distributions of dipole of water in carbon nanotubes, where (a) and (b) denote, respectively, those in (6,6) and (7,7) carbon nanotubes
3.2 径向分布函数
径向分布函数是描述分子体系结构的一个重要参数. 椭圆柱状碳纳米管内水分子的径向分布函数如图3所示, 其中r表示离碳纳米管壁的距离, 由于水分子无法通过e=0.5的(6,6)型碳纳米管, 所以图中无该条件下的径向分布函数曲线. 由图3(a,b)均可以发现: 两种管径下离碳管壁0.26 nm范围内没有水分子出现, 并且当碳纳米管接近圆柱状时该范围增大, 这表明水分子在该范围内具有较高的势能和该范围大小与碳纳米管离心率有关. 同时, 还发现同一e值下(6,6)型碳纳米管的g(r)值均比(7,7)的大, 这说明水分子通过小管径时其聚集程度高. 由图3(a)可知: 当e=0.6时g(r)存在两个峰, 第一个为尖峰并位于r=0.32 nm处, 而第二个是平峰, 其范围为0.40-0.48 nm, 并且第一个峰的强度比第二个峰的大; 当e=1.8和e=2.0的径向分布曲线重合, 并且存在强度相同的两个峰; 当0.8≤e≤1.5时, 其径向分布函数只存在一个峰, 并且强度随着e的增加先增加后减小, 其临界状态为e=1时. 这表明(6,6)型碳纳米管越扁, 管内水分子沿径向存在两种运输状态, 即存在两条水链, 当碳纳米管接近圆柱状时管内水分子以单条水链运输且其与碳纳米管的距离增加. 由图3(b)可知: 当e=0.5时g(r)存在两个峰, 第一个峰位于r=0.34 nm, 第二个峰位于0.48 nm, 并且第一个峰的强度明显大于第二个峰值; 当e=0.6时g(r)只存在一个峰, 并且峰的强度与e=0.5的第一个峰的强度相同, 但是峰所处的位置增加为r=0.41 nm; 当e=0.8和e=1.2时, 径向分布函数均存在两个峰, 对应峰的位置相同, 且第一个峰的强度均大于第二个峰, 但是当e=1时, 第一个峰的强度小于第二个峰; 当e>1.2时, g(r)均只有一个峰且峰的位置相同. 这表明当(7,7)型碳纳米管接近圆柱状时管内水分子存在两种输运状态, 当其越扁时(除e=0.5外), (7,7)型碳纳米管只存在一种运输状态, 该结论与(6,6)型碳纳米管相反.
3.3 水分子通过碳纳米管的流量


图3 不同离心率的碳纳米管壁与其内部水分子(C-O)的径向分布函数, 其中图(a)为(6,6)型碳纳米管, 并且e=1.8和e=2.0的径向分布曲线重合; 图(b)为(7,7)型碳纳米管的径向分布函数Fig. 3 The radial distribution functions (RDFs) of water in carbon nanotubes, where (a) is that in (6,6) carbon nanotubes and the RDF of e=1.8 coincides with e=2.0. (b) is that in (7,7) carbon nanotubes
水分子沿z轴正方向通过不同椭圆柱状碳纳米管的流量如图4所示, 由图可以发现: 水分子通过圆柱形的(6,6)型碳纳米管的流量小于通过(7,7)型的, 该结论与王俊等人[5]一致, 且同一e值下水分子通过碳纳米管的流量随着管径的增加而增加; (6,6)型碳纳米管当e=0.5时流量为0, 这表明在该种情况下水分子无法通过碳纳米管, 这是因为此碳纳米管的短径小于0.26 nm, 同时也发现当e<0.8的(6,6)型碳纳米管流量随着e值的增加而增加, 但是当e>0.8时其流量几乎不变; 然而对于(7,7)型碳纳米管的流量是随着e值的增加先增加后减小最后达到恒定值, 并且流量最大时是e=1时即碳纳米管为圆柱状时. 分析认为可以通过在一定范围内改变碳纳米管的离心率来调节水分子通过碳纳米管的流量从而起到分子开关的作用.
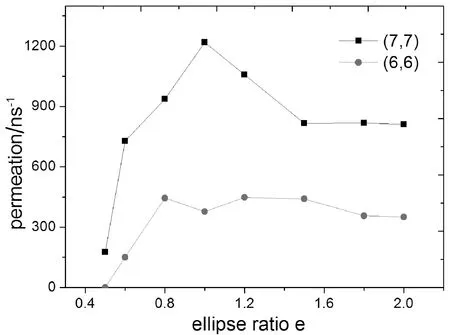
图4 碳纳米管的离心率与水分子的流量的关系Fig. 4 The relationship between water permeation and ellipse ratio of carbon nanotubes
4 结 论
本文通过分子动力学的方法研究了水分子通过形变碳纳米管的运输行为, 即探究碳纳米管的离心率e与管内水分子的偶极矩概率分布、径向函数分布和流量的关系. 结果表明(6,6)型碳纳米管内水分子负偶极矩态在e=1.2时强于正偶极矩态, 其它均为负偶极矩态弱于正偶极矩态, 甚至没有负偶极矩态的出现; 当该手性矢量的碳纳米管越扁时(除e=0.5外)有两条水链的出现, 接近圆柱状或为圆柱状时只有一条链出现, 因为当e=0.5时没有水分子通过碳纳米管; 同时发现管内水分子的流量随e的增加而增加最后保持不变. 然而手性矢量为(7,7)的碳纳米管未出现负偶极矩态强于正偶极矩态的情况; 并当其接近圆柱状时管内水分子存在两条水链的输运状态, 当碳纳米管越扁时(除e=0.5外)只存在单链的运输状态, 该结论与手性矢量为(6,6)型碳纳米管相反, 同时发现其流量随着e值的增加先增加后减小最后达到恒定值, 并且为圆柱状时流量最大. 分析认为椭圆柱状碳纳米管的离心率变化使管内水分子的偶极矩态及其运输状态发生变化; 同时也发现在一定范围内使碳纳米管的离心率改变而起到分子开关的作用. 本文的研究对认识生命的新陈代谢活动、海水淡化和纳米运输器件有着重要的参考作用.
[1] Zhu F Q, Schulten K. Water and proton conduction through carbon nanotubes as models for biological channels[J].BiophysicalJournal, 2003, 85: 236.
[2] Hummer G, Rasaiah J C, Noworyta J P. Water conduction through the hydrophobic channel of a carbon nanotube[J].Nature, 2001, 414: 188.
[3] Li J Y, Gong X J, Lu H J,etal. Electrostatic gating of a nanometer water channel[J].Proc.Natl.Acad.Sci.USA, 2007, 104: 3687.
[4] Zhou Y, Dong S L. Molecular dynamics simulation of water conduction within carbon nanotube[J].ChineseScienceBulletin, 2013, 58 (1): 59.
[5] Wang J, Zhu Y, Zhou J,etal. Diameter and helicity effects on static properties of water molecules confined in carbon nanotubes[J].Phys.Chem.Chem.Phys., 2004, 6: 829.
[6] Nicholls W D, Borg M K, Lockerby D A,etal. Water transport through (7,7) carbon nanotubes of different lengths using molecular dynamics[J].MicrofluidicsandNanofluidics, 2012, 12: 257.
[7] Silva L B D. Structural and dynamical properties of water confined in carbon nanotubes[J].J.Nanostruct.Chem., 2014, 4: 104.
[8] Yuan H J, Dong S L. Molecular dynamic simulation of water molecular confined in carbon nanotubes[J].JournalofQingdaoUniversity:NaturalScienceEdition, 2007, 20(2): 42 (in Chinese)[袁虹君, 董顺乐. 受限于纳米碳管中水的分子动力学模拟[J]. 青岛大学学报: 自然科学版, 2007, 20(2): 42]
[9] Xu K, Wang Q S, Tan B,etal. Molecular dynamic of selectivity and permeation based on deformed carbon nanotube[J].ActaPhys.Sin., 2012, 61(9):096101 (in Chinese) [徐葵, 王青松, 谭兵, 等. 形变碳纳米管选择通过性的分子动力学研究[J]. 物理学报, 2012, 61(9): 096101]
[10] Wang S, Lu H J, TU Y S,etal. Gating of water flow induced by bending of a carbon nanotube[J].Chin.Phys.Lett., 2009, 26(6): 068702.
[11] He J X, Lu H J, Liu Y,etal. Asymmetry of the water flux induced by the deformation of a nanotube[J].Chin.Phys. B, 2012, 21(5): 054703.
[12] Ganesh E N. Single walled and multi walled carbon nanotube structure, synthesis and applications[J].InternationalJournalofInnovativeTechnologyandExploringEngineering, 2013, 2(4): 311.
[13] Zhong W R, Zhang M P, Zheng D Q,etal. Thermal conductivity of deformed carbon nanotubes[J].J.Appl.Phys., 2011, 109(7): 074317.
[14] Zhu F Q, Tajkhorshid E, Schulten K. Pressure-induced water transport in membrane channels studied by molecular dynamics[J].BiophysicalJournal, 2002, 83(5): 154.
Research on the transport behavior of water in the deformed carbon nanotubes
YU You-Sheng, YUE Li, ZHANG Hong-Yun, YIN Hai-Feng, ZENG Fan-Ju, ZHANG Song
(College of Physics and Electronic Engineering, Kaili University, Kaili 556011, China)
The transport behavior of water through the carbon nanotubes play an important role for understanding the metabolic activity in the life, desalination and nano-transport devices. The aim of this paper is to investigate the transport behavior of water in the deformed carbon nanotubes, namely the ellipse ratio of elliptic carbon nanotubes effect on the transport behaviors, by molecular dynamic simulation. It is found that the ellipse ratio has great influence on the probability distribution of dipole, the radial distribution function and the permeation. It is shown that the deformed carbon nanotubes can change the dipole moment state and transport status of water in carbon nanotubes.It is also found that carbon nanotubes can as an on-off of molecules by change there shape in certain range.
Carbon nanotube; Water molecule; Transport behavior; Deformed
2014-09-01
贵州省科学技术联合基金(黔科合LH字[2014]7225);贵州省科学技术基金(黔科合J字[2014]2147);凯里学院博士基金(BS201329); 凯里学院规划基金(Z1234); 凯里学院原子与分子物理重点学科建设项目(KZD2014002)
余幼胜(1985—),男,安徽潜山人,讲师,硕士,主要从事凝聚态物理研究. E-mail: yuyoushengtt@163.com
103969/j.issn.1000-0364.2015.10.012
O552.4; O469
A
1000-0364(2015)05-0791-05
